前章では、勾配降下法を用いてニューラルネットワークが重みとバイアスをどのように学習するかを説明しました。 しかし、その説明にはギャップがありました。具体的には、コスト関数の勾配をどのように計算するかを議論していません。これはとても大きなギャップです！ 本章では、逆伝播と呼ばれる、コスト関数の勾配を高速に計算するアルゴリズムを説明します。

逆伝播アルゴリズムはもともと1970年代に導入されました。 しかし逆伝播が評価されたのは、 David Rumelhart・ Geoffrey Hinton・ Ronald Williams による1986年の著名な論文が登場してからでした。 その論文では、逆伝播を用いると既存の学習方法よりもずっと早く学習できる事をいくつかのニューラルネットワークに対して示し、それまでニューラルネットワークでは解けなかった問題が解ける事を示しました。 今日では、逆伝播はニューラルネットワークを学習させる便利なアルゴリズムです。

本章は他の章に比べて数学的に難解です。 よほど数学に対し熱心でなければ、本章を飛ばして、逆伝播を中身を無視できるブラックボックスとして扱いたくなるかもしれません。 では、なぜ時間をかけて逆伝播の詳細を勉強するのでしょうか？

その理由はもちろん理解のためです。 逆伝播の本質はコスト関数$C$のネットワークの重み$w$（もしくはバイアス$b$）に関する偏微分$\partial C / \partial w$ （$\partial C / \partial b$）です。 偏微分をみると、重みとバイアスを変化させた時のコスト関数の変化の度合いがわかります。 偏微分の式は若干複雑ですが、そこには美しい構造があり、式の各要素には自然で直感的な解釈を与える事ができます。 そうです、逆伝播は単なる高速な学習アルゴリズムではありません。 逆伝播をみることで、重みやバイアスを変化させた時のニューラルネットワーク全体の挙動の変化に関して深い洞察が得られます。 逆伝播を勉強する価値はそこにあるのです。

そうは言うものの、本章をざっと読んだり、読み飛ばして次の章に進んでも大丈夫です。 この本は逆伝播をブラックボックスとして扱っても他の章を理解できるように書いています。 もちろん次章以降で本章の結果を参照する部分はあります。 しかし、その参照部分の議論をすべて追わなくても、主な結論は理解できるはずです。

ウォーミングアップ：ニューラルネットワークの出力の行列を用いた高速な計算

逆伝播を議論する前に、ニューラルネットワークの出力を高速に計算する行列を用いたアルゴリズムでウォーミングアップしましょう。 私達は 前章の最後のあたり で既にこのアルゴリズムを簡単に見ています。 しかしその時はざっと書いていたので、ここで立ち戻って詳しく説明しようと思います。 特にこれまで説明して慣れた文脈で逆伝播で使用する記号に慣れるのに、このウォーミングアップは良い方法です。

ニューラルネットワーク中の重みを曖昧性なく指定する表記方法からまず始めましょう。 $w^l_{jk}$で、$(l-1)$番目の層の$k$番目のニューロンから、$l$番目の層の$j$番目のニューロンへの接続に対する重みを表します。 例えば下図は、2番目の層の4番目のニューロンから、3番目の層の2番目のニューロンへの接続の重みを表します。

この表記方法は最初は面倒で、使いこなすのにある程度の練習が必要かもしれません。 しかし、少し頑張ればこの表記方法は簡単で自然だと感じるようになるはずです。 この表記方法で若干曲者なのが、$j$と$k$の順番です。 $j$を入力ニューロン、$k$を出力ニューロンとする方が理にかなっていると思うかもしれませんが、 実際には逆にしています。 奇妙なこの記述方法の理由は後程説明します。

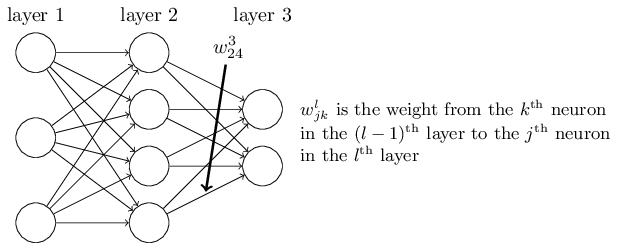
ニューラルネットワークのバイアスと活性についても似た表記方法を導入します。 具体的には、$b^l_j$で$l$番目の層の$j$番目のニューロンのバイアスを表します。 また、$a^l_j$で$l$番目の層の$j$番目のニューロンの活性を表します。 下図はこれらの表記方法の利用例です。

これらの表記を用いると、$l$番目の層の$j$番目のニューロンの活性$a^l_j$は、$(l-1)$番目の層の活性と以下の式で関係付けられます（式 (4) \begin{eqnarray} \frac{1}{1+\exp(-\sum_j w_j x_j-b)} \nonumber \end{eqnarray} と前章の周辺の議論を比較してください） \begin{eqnarray} a^{l}_j = \sigma\left( \sum_k w^{l}_{jk} a^{l-1}_k + b^l_j \right). \tag{23}\end{eqnarray} ここで、和は$(l-1)$番目の層の全てのニューロン$k$について足しています。 この式を行列で書き直すため、各層$l$に対し重み行列$w^l$を定義します。 重み行列$w^l$の各要素は$l$番目の層のニューロンを終点とする接続の重みです。 すなわち、$j$行目$k$列目の要素を$w^l_{jk}$とします。 同様に、各層$l$に対し、バイアスベクトル$b^l$を定義します。 おそらく想像できると思いますが、バイアスベクトルの要素は$b^l_j$達で、 $l$番目の層の各ニューロンに対し1つの行列要素が伴います。 最後に、活性ベクトル$a^l$を活性$a^l_j$達で定義します。

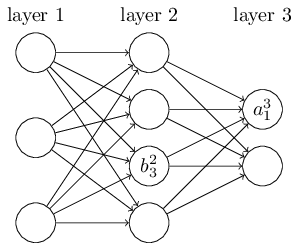
(23) \begin{eqnarray} a^{l}_j = \sigma\left( \sum_k w^{l}_{jk} a^{l-1}_k + b^l_j \right) \nonumber \end{eqnarray} を行列形式に書き直すのに必要な最後の要素は、$\sigma$などの関数のベクトル化です。 ベクトル化は既に前章で簡単に見ました。 要点をまとめると、$\sigma$のような関数をベクトル$v$の各要素に適用したいというのがアイデアです。 このような各要素への関数適用には$\sigma(v)$という自然な表記を用います。 つまり、$\sigma(v)$の各要素は$\sigma(v)_j = \sigma(v_j)$です。 例えば$f(x) = x^2$とすると、次のようになります。 \begin{eqnarray} f\left(\left[ \begin{array}{c} 2 \\ 3 \end{array} \right] \right) = \left[ \begin{array}{c} f(2) \\ f(3) \end{array} \right] = \left[ \begin{array}{c} 4 \\ 9 \end{array} \right]. \tag{24}\end{eqnarray} すなわち、ベクトル化した$f$はベクトルの各要素を2乗します。

この表記方法を用いると、式 (23) \begin{eqnarray} a^{l}_j = \sigma\left( \sum_k w^{l}_{jk} a^{l-1}_k + b^l_j \right) \nonumber \end{eqnarray} は次のような美しくコンパクトなベクトル形式で書けます。 \begin{eqnarray} a^{l} = \sigma(w^l a^{l-1}+b^l). \tag{25} \end{eqnarray} この表現を用いると、ある層の活性とその前の層の活性との関係を俯瞰できます。 我々が行っているのは活性に対し重み行列を掛け、バイアスベクトルを足し、最後に$\sigma$関数を適用するだけです。 *ところで、先ほどの$w^l_{jk}$という奇妙な表記を用いる動機はこの式に由来します。 もし、$j$を入力ニューロンに用い、$k$を出力ニューロンに用いたとすると、式 (25) \begin{eqnarray} a^{l} = \sigma(w^l a^{l-1}+b^l) \nonumber \end{eqnarray} は重み行列をそれの転置行列に置き換えなければなりません。 些細な変更ですが、煩わしい上に「重み行列を掛ける」と簡単に言ったり（もしくは考えたり）できなくなってしまいます。 この見方はこれまでのニューロン単位での見方よりも簡潔で、添字も少なくて済みます。 議論の正確性を失う事なく添字地獄から抜け出せる方法と考えると良いでしょう。 さらに、この表現方法は実用上も有用です。 というのも、多くの行列ライブラリでは高速な行列掛算・ベクトル足し算・関数のベクトル化の実装が提供されているからです。 実際、前章のコード では、ネットワークの挙動の計算にこの表式を暗に利用していました。

$a^l$の計算のために式 (25)\begin{eqnarray} a^{l} = \sigma(w^l a^{l-1}+b^l) \nonumber\end{eqnarray} を利用する時には、途中で$z^l \equiv w^l a^{l-1}+b^l$を計算しています。 この値は後の議論で有用なので名前をつけておく価値があります。 $z^l$を$l$番目の層に対する重みつき入力と呼ぶことにします。 本章の以降の議論では重みつき入力$z^l$を頻繁に利用します。 式 (25)\begin{eqnarray} a^{l} = \sigma(w^l a^{l-1}+b^l) \nonumber\end{eqnarray} をしばしば重み付き入力を用いて$a^l = \sigma(z^l)$とも書きます。 $z^l$の要素は$z^l_j = \sum_k w^l_{jk} a^{l-1}_k+b^l_j$と書ける事にも注意してください。 つまり、$z^l_j$は$l$番目の層の$j$番目のニューロンが持つ活性関数へ与える重みつき入力です。

コスト関数に必要な2つの仮定

逆伝播の目標はニューラルネットワーク中の任意の重み$w$またはバイアス$b$に関するコスト関数$C$の偏微分、すなわち$\partial C / \partial w$と$\partial C / \partial b$の計算です。 逆伝播が機能するには、コスト関数の形について2つの仮定を置く必要があります。 それらの仮定を述べる前に、コスト関数の例を念頭に置くのが良いでしょう。 前章でも出てきた2乗コスト関数（参考：式(6)\begin{eqnarray} C(w,b) \equiv） \frac{1}{2n} \sum_x \| y(x) - a\|^2 \nonumber\end{eqnarray}）をここでも考えます。 前章の記法では、2乗コスト関数は以下の様な形をしていました \begin{eqnarray} C = \frac{1}{2n} \sum_x \|y(x)-a^L(x)\|^2. \tag{26}\end{eqnarray} ここで、$n$は訓練例の総数、和は個々の訓練例$x$について足しあわせたもの、$y = y(x)$は対応する目標の出力、$L$はニューラルネットワークの層数、$a^L = a^L(x)$は$x$を入力した時のニューラルネットワークの出力のベクトルです。

では、逆伝播を適用するために、コスト関数$C$に置く仮定はどのようなものでしょうか。 1つ目の仮定はコスト関数は個々の訓練例$x$に対するコスト関数$C_x$の平均 $C = \frac{1}{n} \sum_x C_x$で書かれているという事です。 2乗コスト関数ではこの仮定が成立しています。 それには1つの訓練例に対するコスト関数を$C_x = \frac{1}{2} \|y-a^L \|^2$とすれば良いです。 この仮定はこの本で登場する他のコスト関数でも成立しています。

この仮定が必要となる理由は、逆伝播によって計算できるのは個々の訓練例に対する偏微分$\partial C_x / \partial w$、$\partial C_x / \partial b$だからです。 コスト関数の偏微分$\partial C / \partial w$、$\partial C / \partial b$は全訓練例についての平均を取ることで得られます。 この仮定を念頭に置き、私達は訓練例$x$を1つ固定していると仮定し、コスト$C_x$を添字$x$を除いて$C$と書くことにします。最終的に除いた$x$は元に戻しますが、当面は記法が煩わしいので暗に$x$が書かれていると考えます。

コスト関数に課す2つ目の仮定は、コスト関数はニューラルネットワークの出力の関数で書かれているという仮定です。

例えば、2乗誤差関数はこの要求を満たしています、それは1つの訓練例$x$に対する誤差は以下のように書かれるためです \begin{eqnarray} C = \frac{1}{2} \|y-a^L\|^2 = \frac{1}{2} \sum_j (y_j-a^L_j)^2. \tag{27}\end{eqnarray} もちろんこのコスト関数は目標とする出力$y$にも依存しています。 コスト関数を$y$の関数とみなさない事を不思議に思うかもしれません。 しかし、訓練例$x$を固定する事で、出力$y$も固定している事に注意してください。 つまり、出力$y$は重みやバイアスをどのように変化させた所で変化させられる量ではなく、ニューラルネットが学習するものではありません。 ですので、$C$を出力の活性$a^L$単独の関数とみなし、$y$は関数を定義するための単なるパラメータとみなすのは意味のある問題設定です。

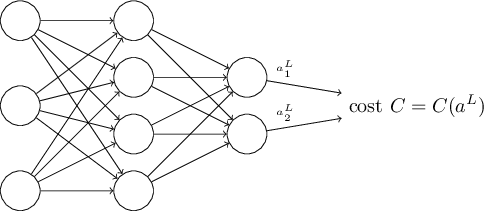
アダマール積 $s \odot t$

逆伝播アルゴリズムは、ベクトルの足し算やベクトルと行列の掛け算など、一般的な代数操作に基づいています。 しかし、その中で1つあまり一般的ではない操作があります。 $s$と$t$が同じ次元のベクトルとした時、$s \odot t$を2つのベクトルの要素ごとの積とします。つまり、$s \odot t$の要素は$(s \odot t)_j = s_j t_j$です。 例えば、 \begin{eqnarray} \left[\begin{array}{c} 1 \\ 2 \end{array}\right] \odot \left[\begin{array}{c} 3 \\ 4\end{array} \right] = \left[ \begin{array}{c} 1 * 3 \\ 2 * 4 \end{array} \right] = \left[ \begin{array}{c} 3 \\ 8 \end{array} \right] \tag{28}\end{eqnarray} です。 この種の要素ごとの積はしばしばアダマール積、もしくはシューア積と呼ばれます。 私達はアダマール積と呼ぶことにします。 よく出来た行列ライブラリにはアダマール積の高速な実装が用意されており、逆伝播を実装する際に手軽に利用できます。

逆伝播の基礎となる4つの式

逆伝播は重みとバイアスの値を変えた時にコスト関数がどのように変化するかを把握する方法です。 これは究極的には$\partial C / \partial w^l_{jk}$と$\partial C / \partial b^l_j$とを計算する事を意味します。 これらの偏微分を計算する為にまずは中間的な値$\delta^l_j$を導入します。 この値は$l$番目の層の$j$番目のニューロンの誤差と呼びます。 逆伝播の仕組みを見ると$\delta^l_j$を計算手順と$\delta^l_j$を$\partial C/ \partial w^l_{jk}$や$\partial C / \partial b^l_j$と関連づける方法が得られます。

誤差の定義方法を理解する為にニューラルネットワークの中にいる悪魔を想像してみましょう。

悪魔は$l$番目の層の$j$番目のニューロンに座っているとします。 ニューロンに入力が入ってきた時、悪魔はニューロンをいじって、重みつき入力に小さな変更$\Delta z^l_j$を加えます。 従って、ニューロンは$\sigma(z^l_j)$の代わりに、$\sigma(z^l_j+\Delta z^l_j)$を出力します。 この変化はニューラルネット中の後段の層に伝播し、最終的に全体のコスト関数の値は$\frac{\partial C}{\partial z^l_j} \Delta z^l_j$だけ変化します。

ここで、この悪魔は善良な悪魔で、コスト関数を改善する、つまりコストを小さくするような$\Delta z^l_j$を探そうとするとします。 $\frac{\partial C}{\partial z^l_j}$が大きな値（正でも負も良いです）であるとします。 すると、$\frac{\partial C}{\partial z^l_j}$と逆の符号の$\Delta z^l_j$を選ぶことで、この悪魔はコストをかなり改善させられます。 逆に、もし$\frac{\partial C}{\partial z^l_j}$が$0$に近いと悪魔は重みつき入力$z^l_j$を摂動させてもコストをそれほどは改善できません。 悪魔が判断できる範囲においてはニューロンは既に最適に近い状態だと言えます* *もちろんこれが正しいのは$\Delta z^l_j$が小さい場合に限ってです。悪魔は微小な変化しか起こせないと仮定しています。 つまり、ヒューリスティックには、$\frac{\partial C}{\partial z^l_j}$はニューラルネットワークの誤差を測定しているという意味を与える事ができます。

この話を動機として、$l$番目の層の$j$番目のニューロンの誤差$\delta^l_j$を以下のように定義します \begin{eqnarray} \delta^l_j \equiv \frac{\partial C}{\partial z^l_j}. \tag{29}\end{eqnarray}. 慣習に沿って、$\delta^l$で$l$番目の層の誤差からなるベクトルを表します。 逆伝播により、各層での$\delta^l$を計算し、これらを真に興味のある$\partial C / \partial w^l_{jk}$や$\partial C / \partial b^l_j$と関連付けることができます。

悪魔はなぜ重みつき入力$z^l_j$を変えようとするのかを疑問に思うかもしれません。 確かに、出力活性$a^l_j$を変化させ、その結果の$\frac{\partial C}{\partial a^l_j}$を誤差の指標として用いる方が自然かもしれません。 実際そのようにしても、以下の議論は同じように進められます。 しかし、やってみるとわかるのですが、誤差逆伝播の表示が数学的に若干複雑になってしまいます。 ですので、我々は誤差の指標として$\delta^l_j = \frac{\partial C}{\partial z^l_j}$を用いることにします* *MNISTのような分類問題では、誤差（error）という言葉はしばしば誤分類の割合を意味します。 例えばニューラルネットが96.0%の数字を正しく分類できたとしたら、"error"は4.0%です。 もちろん、これは$\delta$ベクトルとは全く異なる意味です。 実際の文脈ではどちらの意味かで迷うことはないでしょう。 。

攻略計画 逆伝播は4つの基本的な式を基礎とします。 これらを組み合わせると、誤差$\delta^l$とコスト関数の勾配を計算ができます。 以下でその4つの式を挙げていきますが、1点注意があります：これらの式の意味をすぐに消化できると期待しない方が良いでしょう。 そのように期待するとがっかりするかもしれません。 逆伝播は内容が豊富であり、これらの式は相当の時間と忍耐がかけて徐々に理解できていくものです。 幸いなことに、ここで辛抱しておくと後々何度も報われることになります。 この節の議論はスタート地点に過ぎませんが、逆伝播の式を深く理解する過程の中で役に立つもののはずです。

誤差逆伝播の式をより深く理解する方法の概略は以下の通りです。 まず、 これらの式の手短な証明を示します。 この証明を見ればなぜこれらの式が正しいのかを理解しやすくなります。 その後、これらの式を擬似コードで書き直し、 その擬似コードをどのように実装できるかを実際のPythonのコードで示します。 本章の最後の節では、誤差逆伝播の式の意味を直感的な図で示し、ゼロからスタートしてどのように誤差逆伝播を発見するかを見ていきます。 その道中で、我々は何度も4つの基本的な式に立ち戻ります。 理解が深まるにつれ、これらの式が快適で、美しく自然なものとさえ思えるようになるはずです。

出力層での誤差$\delta^L$に関する式： $\delta^L$の各要素は \begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j). \tag{BP1}\end{eqnarray} です。 これはとても自然な表式です。右辺の第1項の$\partial C / \partial a^L_j$はコストが$j$番目の出力活性の関数としてどの程度敏感に変化するかの度合いを測っています。 例えば、$C$が出力層の特定のニューロン（例えば$j$番目とします）にそれほど依存していなければ、我々の期待通り$\delta^L_j$は小さくなります。 一方、右辺の第2項の$\sigma'(z^L_j)$は活性関数$\sigma$が$z^L_j$の変化にどの程度敏感に反応するかの度合いを表しています。

ここで注目すべきなのは (BP1)\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \nonumber\end{eqnarray} 中の全ての項が簡単に計算できる事です。 ニューラルネットワークの挙動を計算する間に$z^L_j$を計算でき、さらに若干のオーバーヘッドを加えれば$\sigma'(z^L_j)$も計算できます。従って、第2項は計算できます。 第1項に関してですが、$\partial C / \partial a^L_j$の具体的な表式はもちろんコスト関数の形に依存します。しかし、コスト関数が既知ならば$\partial C / \partial a^L_j$を計算するのは難しくありません。 例えば、2乗誤差コスト関数を用いた場合、$C = \frac{1}{2} \sum_j (y_j-a_j)^2$なので、$\partial C / \partial a^L_j = (a_j-y_j)$という簡単に計算できる式が得られます。

式(BP1)\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \nonumber\end{eqnarray} は$\delta^L$の各要素に対する表式です。 この表式自体は悪くはないのですが、逆伝播で欲しい行列を用いた表式ではありません。 この式を行列として書き直すのは容易で、以下の様に書けます \begin{eqnarray} \delta^L = \nabla_a C \odot \sigma'(z^L). \tag{BP1a}\end{eqnarray} ここで、$\nabla_a C$は偏微分$\partial C / \partial a^L_j$を並べたベクトルです。 $\nabla_a C$は出力活性に対する$C$の変化率とみなせます。 (BP1a)\begin{eqnarray} \delta^L = \nabla_a C \odot \sigma'(z^L) \nonumber\end{eqnarray} と (BP1)\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \nonumber\end{eqnarray} は同値である事はすぐにわかります。ですので、以下では両者の式を参照するのに (BP1)\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \nonumber\end{eqnarray} を用いる事にします。 例として、2乗誤差コスト関数の例では$\nabla_a C = (a^L-y)$です。 従って行列形式の (BP1)\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \nonumber\end{eqnarray} は以下のようになります。 \begin{eqnarray} \delta^L = (a^L-y) \odot \sigma'(z^L). \tag{30}\end{eqnarray} 見ての通り、この表式内の全ての項がベクトル形式の表式となっており、Numpyなどのライブラリで簡単に計算できます。

誤差$\delta^{l}$の次層での誤差$\delta^{l+1}$に関する表式： これは以下の通りです \begin{eqnarray} \delta^l = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l). \tag{BP2}\end{eqnarray} ここで、$(w^{l+1})^T$は$(l+1)$番目の層の重み行列$w^{l+1}$の転置です。 この式は一見複雑ですが、各要素はきちんとした解釈を持ちます。 $(l+1)$番目の層の誤差$\delta^{l+1}$番目が既知だとします。 重み行列の転置$(w^{l+1})^T$を掛ける操作は、直感的には誤差をネットワークとは逆方向に伝播させていると考える事ができます。 従って、この値は$l$番目の層の出力の誤差を測る指標の一種とみなすことができます。 転置行列を掛けた後、$\sigma'(z^l)$とのアダマール積を取っています。 これにより$l$番目の層の活性関数を通してエラーを更に逆方向に伝播しています。 その結果、$l$番目の層の重みつき入力についての誤差$\delta^l$が得られます。

(BP2)\begin{eqnarray} \delta^l = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l) \nonumber\end{eqnarray} を (BP1)\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \nonumber\end{eqnarray} と組み合わせる事で、ニューラルネットワークの任意の層$l$での誤差$\delta^l$を計算できます。 まず、$\delta^L$を式 (BP1)\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j). \nonumber\end{eqnarray} で計算します。 次に、式 (BP2)\begin{eqnarray} \delta^l = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l) \nonumber\end{eqnarray} を適用して$\delta^{L-1}$を計算します。 その後、再び (BP2)\begin{eqnarray} \delta^l = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l) \nonumber\end{eqnarray} を適用して、$\delta^{L-2}$を計算します。以下これを繰り返してニューラルネットワークを逆向きに辿る事ができます。

任意のバイアスに関するコストの変化率の式： 具体的には以下の通りです \begin{eqnarray} \frac{\partial C}{\partial b^l_j} = \delta^l_j. \tag{BP3}\end{eqnarray} すなわち、誤差$\delta^l_j$はコスト関数の変化率$\partial C / \partial b^l_j$と完全に同一です。 (BP1)\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \nonumber\end{eqnarray} と (BP2)\begin{eqnarray} \delta^l = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l) \nonumber\end{eqnarray} からこの値の計算方法は既にわかっているので、この事実はは好都合です。 (BP3)\begin{eqnarray} \frac{\partial C}{\partial b^l_j} = \delta^l_j \nonumber\end{eqnarray} を簡潔に \begin{eqnarray} \frac{\partial C}{\partial b} = \delta \tag{31}\end{eqnarray} と書くことができます。ここで、$\delta$の各成分は同じニューロンのバイアス$b$で評価した値と解釈します。

任意の重みについてのコストの変化率： 具体的には以下の通りです。 \begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j. \tag{BP4}\end{eqnarray} この式を見ると、偏微分$\partial C / \partial w^l_{jk}$を計算方法が既知の$\delta^l$と$a^{l-1}$を用いて計算できることがわかります。 この式はもう少し添字の軽い式で \begin{eqnarray} \frac{\partial C}{\partial w} = a_{\rm in} \delta_{\rm out}, \tag{32}\end{eqnarray} と書き直せます。ここで、$a_{\rm in}$は重み$w$を持つ枝に対する入力ニューロンの活性で、$\delta_{\rm out}$は同じ枝に対する出力ニューロンの持つ誤差です。 重み$w$とそれに接続する2つのニューロンだけに焦点を絞ると、この式は以下のように見ることができます：

式 (32)\begin{eqnarray} \frac{\partial C}{\partial w} = a_{\rm in} \delta_{\rm out} \nonumber\end{eqnarray} から$a_{\rm in}$が小さい($a_{\rm in} \approx 0$)時には、勾配$\partial C / \partial w$も小さくなる傾向があるという結論が得られます。 このような状態を重みの学習が遅いと表現します。その意味は、勾配降下法を行っている間、値が大きく変化しないという事です。 同じ事の言い換えですが、式 (BP4)\begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j \nonumber\end{eqnarray} の帰結の1つとして、活性の低いニューロンから入力を受けとる重みは学習が遅いとわかります。

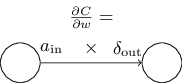
(BP1)\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \nonumber\end{eqnarray} - (BP4)\begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j \nonumber\end{eqnarray} からわかる事は他にもあります。 出力層から見てみましょう。 (BP1)\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \nonumber\end{eqnarray} 内の$\sigma'(z^L_j)$の項に注目します。 前章のシグモイド関数のグラフを思い出すと、$\sigma(z^L_j)$が$0$か$1$に近づくとき関数$\sigma$はとても平坦になっていました。 これは$\sigma'(z^L_j) \approx 0$の状態です。 従って、出力ニューロンの活性が低かったり($\approx 0$)、高かったり($\approx 1$)すると、最終層の学習は遅い事がわかります。 このような状況を、出力ニューロンは飽和し、重みの学習が終了している（もしくは重みの学習が遅い）と表現するのが一般的です。 同様の事は出力ニューロンのバイアスに対しても成立します。

出力層より前の層でも似た考察ができます。特に (BP2)\begin{eqnarray} \delta^l = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l) \nonumber\end{eqnarray} 内の$\sigma'(z^l)$の項に注目します。 この式は、ニューロンが飽和状態だと$\delta^l_j$は小さくなる傾向がある事を意味します。また、さらに飽和状態のニューロンに入力される重みの学習も遅くなることを意味します*。 *$(w^{l+1})^T \delta^{l+1}$が十分大きく、$\sigma'(z^l_j)$が小さくてもその埋め合わせができるならば、この推論は成り立ちません。ここでは一般的な傾向について述べています。。

まとめると、入力ニューロンが低活性状態であるか、出力ニューロンが飽和状態（低活性もしくは高活性状態）の時には、重みの学習が遅いという事がわかりました。

これらの知見はどれも極端に驚くべき事ではありません。 しかし、これらの考察を通じてニューラルネットワークの学習過程に関するメンタルモデルの精緻にできます。 さらに、以上の考察を逆向きに利用する事ができます。 これら4つの基本方程式は任意の活性化関数について成立します （後述のように、証明に関数$\sigma$の特別な性質を用いていないからです）。 従って、これらの式を利用して好きな学習特性を持つ活性化関数を設計する事が可能です。 アイデアを示すために例を挙げると、例えば（シグモイドではない）活性化関数$\sigma$として$\sigma'$が常に正で、$0$に漸近しないものを選んだとします。 すると、通常のシグモイド関数を用いたニューロンが飽和した際に起こってしまう学習の減速を防ぐ事が可能です。 この本の後ろでは、この種の修正を活性化関数に対して施します。 (BP1)\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \nonumber\end{eqnarray} - (BP4)\begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j \nonumber\end{eqnarray} の4つの式を覚えておくと、なぜこのような修正を行うのか、修正でどのような影響が起こるかを説明するのに役立ちます。

問題

• 誤差逆伝播の別の表示方法： これまで、誤差逆伝播の式（特に (BP1)\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \nonumber\end{eqnarray} と (BP2)\begin{eqnarray} \delta^l = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l) \nonumber\end{eqnarray} ）をアダマール積を用いて記述していました。 アダマール積に慣れていない読者はこの表式にに戸惑ったかもしれません。 これらの式を通常の行列の掛け算に基づいて表示する別の方法があります。 読者によってはこのアプローチは教育的かもしれません。 (1) (BP1)\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \nonumber\end{eqnarray} を以下の様に書き換えられる事を示してください \begin{eqnarray} \delta^L = \Sigma'(z^L) \nabla_a C \tag{33}\end{eqnarray} ここで、$\Sigma'(z^L)$は$\sigma'(z^L_j)$を対角成分に持ち、非対角成分は$0$の正方行列です。 この行列は$\nabla_a C$に通常の行列の掛け算で作用します。 (2) (BP2)\begin{eqnarray} \delta^l = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l) \nonumber\end{eqnarray} を以下の様に書き換えられる事を示してください \begin{eqnarray} \delta^l = \Sigma'(z^l) (w^{l+1})^T \delta^{l+1}. \tag{34}\end{eqnarray} (3) (1)と(2)を組み合わせて、以下の式を示してください。 \begin{eqnarray} \delta^l = \Sigma'(z^l) (w^{l+1})^T \ldots \Sigma'(z^{L-1}) (w^L)^T \Sigma'(z^L) \nabla_a C \tag{35}\end{eqnarray} 行列の掛け算に慣れている読者にとっては (BP1)\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \nonumber\end{eqnarray} と (BP2)\begin{eqnarray} \delta^l = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l) \nonumber\end{eqnarray} よりも、こちらの方が理解しやすいかもしれません。 それでも (BP1)\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \nonumber\end{eqnarray} と (BP2)\begin{eqnarray} \delta^l = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l) \nonumber\end{eqnarray} の表式を用いたのは、こちらの方が実装時の数値計算が速いからです。

  4つの基本的な式の証明（任意）

  それでは、(BP1)\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \nonumber\end{eqnarray}-(BP4)\begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j \nonumber\end{eqnarray}を証明していきます。 これらはすべて多変数関数の微分の連鎖律の結論です。 もし連鎖律に慣れていたら、読み進める前に自力での導出に挑戦してみるのを強くおすすめします。

  まず、出力での誤差$\delta^L$の表式 (BP1)\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \nonumber\end{eqnarray} から証明しましょう。 この式を示すのに、まず次の式を思い出します \begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial z^L_j}. \tag{36}\end{eqnarray} 連鎖律を適用すると、この微分を出力活性に関する偏微分で書き直す事ができます \begin{eqnarray} \delta^L_j = \sum_k \frac{\partial C}{\partial a^L_k} \frac{\partial a^L_k}{\partial z^L_j}. \tag{37}\end{eqnarray} ここで、和は出力層のすべてのニューロン$k$について足し合わせます。 もちろん、$k=j$の時には、$k$番目のニューロンの出力活性$a^L_k$は、$j$番目のニューロンの重み付き入力$z^L_j$にのみ依存します。 従って、$k\neq j$の時には$\partial a^L_k / \partial z^L_j$の値は$0$です。 結果として前述の式を以下のように簡略化できます \begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \frac{\partial a^L_j}{\partial z^L_j}. \tag{38}\end{eqnarray} $a^L_j = \sigma(z^L_j)$であった事を思い出すと、第2項は$\sigma'(z^L_j)$と書けて、 \begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \tag{39}\end{eqnarray} となります。これを添字なしの形式で書くと (BP1)\begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j) \nonumber\end{eqnarray} が得られます。

  次に、誤差$\delta^l$をその1つ後ろの層の誤差$\delta^{l+1}$を用いて表す (BP2)\begin{eqnarray} \delta^l = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l) \nonumber\end{eqnarray} を証明します。 そのために、連鎖律を用いて$\delta^l_j = \partial C / \partial z^l_j$を$\delta^{l+1}_k = \partial C / \partial z^{l+1}_k$を用いて書き直します \begin{eqnarray} \delta^l_j & = & \frac{\partial C}{\partial z^l_j} \tag{40}\\ & = & \sum_k \frac{\partial C}{\partial z^{l+1}_k} \frac{\partial z^{l+1}_k}{\partial z^l_j} \tag{41}\\ & = & \sum_k \frac{\partial z^{l+1}_k}{\partial z^l_j} \delta^{l+1}_k. \tag{42}\end{eqnarray} ここで、最後の行は2つの項を交換し、第2項を$\delta^{l+1}_k$の定義で置き換えました。 最後の行の第1項を評価するために、次の式に注意します \begin{eqnarray} z^{l+1}_k = \sum_j w^{l+1}_{kj} a^l_j +b^{l+1}_k = \sum_j w^{l+1}_{kj} \sigma(z^l_j) +b^{l+1}_k. \tag{43}\end{eqnarray} この式を微分すると、次が得られます \begin{eqnarray} \frac{\partial z^{l+1}_k}{\partial z^l_j} = w^{l+1}_{kj} \sigma'(z^l_j). \tag{44}\end{eqnarray} この式で (42)\begin{eqnarray} & = & \sum_k \frac{\partial z^{l+1}_k}{\partial z^l_j} \delta^{l+1}_k \nonumber\end{eqnarray} を置き換えると、次の式が得られます \begin{eqnarray} \delta^l_j = \sum_k w^{l+1}_{kj} \delta^{l+1}_k \sigma'(z^l_j). \tag{45}\end{eqnarray} この式を添え字を用いずに書いたものが (BP2)\begin{eqnarray} \delta^l = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l) \nonumber\end{eqnarray} そのものです。

  証明したいあと2つの式は (BP3)\begin{eqnarray} \frac{\partial C}{\partial b^l_j} = \delta^l_j \nonumber\end{eqnarray} と (BP4)\begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j \nonumber\end{eqnarray} です。 これらの式もこれまでの2つの式と似た方法で連鎖律から導けます。 証明は読者にお任せします。

  演習

  • (BP3)\begin{eqnarray} \frac{\partial C}{\partial b^l_j} = \delta^l_j \nonumber\end{eqnarray} と (BP4)\begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j \nonumber\end{eqnarray} を証明してください。

  以上で逆伝播の4つの基本的な式の証明が完了しました。 証明は一見複雑かもしれません。 しかし、これらは連鎖律を慎重に適用した結果にしか過ぎません。 もう少し詳しく言えば、逆伝播は多変数関数の微分で利用される連鎖律をシステマチックに適用する事で、コスト関数の勾配を計算する方法と見る事ができます。 それが逆伝播の正体であり、残りは些細な部分です。

  逆伝播アルゴリズム

  逆伝播の式により、コスト関数の勾配の計算が可能になりました。 その方法を具体的にアルゴリズムの形で書き下してみましょう。

  1. 入力 $x$： 入力層に対応する活性$a^{1}$をセットする

  2. フィードフォワード： 各$l = 2, 3, \ldots, L$に対し、$z^{l} = w^l a^{l-1}+b^l$ and $a^{l} = \sigma(z^{l})$を計算する

  3. 誤差$\delta^L$を出力： 誤差ベクトル$\delta^{L} = \nabla_a C \odot \sigma'(z^L)$を計算する

  4. 誤差を逆伝播： 各$l = L-1, L-2, \ldots, 2$に対し、$\delta^{l} = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^{l})$を計算する

  5. 出力： コスト関数の勾配は $\frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j$と $\frac{\partial C}{\partial b^l_j} = \delta^l_j$ で得られる

  アルゴリズムを見ると、これがなぜ逆伝播と呼ばれるかがわかるでしょう。 最終層から始まり、逆向きに誤差ベクトル$\delta^l$を計算しています。 ネットワークを逆向きに辿るのが奇妙に思われるかもしれません。 しかし、逆伝播の証明を思い返すと、コストはニューラルネットワークの出力についての関数であるという事から、逆伝播の方向が決まっている事がわかります。 前段の重みやバイアスによりコストがどのように変化するかを見るためには、連鎖律を繰り返し適用しなければならず、欲しい計算式を得るにはネットワークを逆方向に辿る必要があります。

  演習

  • ニューロンの1つを差し替えた時の逆伝播： フィードフォワードニューラルネットワークの特定の1つのニューロンを、$f(\sum_j w_j x_j + b)$を出力するものに変更したとします。ここで、$f$はシグモイド以外の適当な関数です。 この場合、逆伝播アルゴリズムはどのように変更すればよいでしょうか。

  • 線形ニューロンでの逆伝播： ニューラルネットワーク内の非線形の$\sigma$関数を$\sigma(z) = z$に変更したとします。 逆伝播アルゴリズムをこの変更にあうように書き直してください。

  前述のように、逆伝播アルゴリズムは単一の訓練例に対するコスト関数$C = C_x$の勾配を計算します。 しかし実際の実装では、逆伝播を、確率的勾配降下法などの多数の訓練例に対する勾配を計算する学習アルゴリズムと組み合わせるのが一般的です。 以下のアルゴリズムでは、$m$個の訓練例からなるミニバッチに対して勾配降下法を適用して学習を行っています。

  1. 訓練例のセットを入力

  2. 各訓練例$x$に対して： 対応する活性$a^{x, 1}$をセットし、以下のステップを行う：
     • フィードフォワード： $l = 2, 3, \ldots, L$に対し、$z^{x,l} = w^l a^{x,l-1}+b^l$と$a^{x,l} = \sigma(z^{x,l})$を計算する

     • 誤差$\delta^{x,L}$を出力： ベクトル$\delta^{x,L} = \nabla_a C_x \odot \sigma'(z^{x,L})$を計算する

     • 誤差を逆伝播する： $l = L-1, L-2, \ldots, 2$に対し、$\delta^{x,l} = ((w^{l+1})^T \delta^{x,l+1}) \odot \sigma'(z^{x,l})$を計算する

  3. 勾配降下： $l = L, L-1, \ldots, 2$に対し、重みを$w^l \rightarrow w^l-\frac{\eta}{m} \sum_x \delta^{x,l} (a^{x,l-1})^T$で更新し、バイアスを$b^l \rightarrow b^l-\frac{\eta}{m} \sum_x \delta^{x,l}$で更新する

  もちろん、確率的勾配降下法を実装する際は、訓練例のミニバッチを作成する外部ループと複数回のエポックで訓練を繰り返す為の外部ループが必要です。 簡単のためにそれらは記述しませんでした。

  逆伝播の実装

  逆伝播の理論を理解した事で、逆伝播の実装に利用した前章のコードを理解できる段階に達しました。 この章を思い出すと、逆伝播の実装はNetworkクラスのupdate_minibatchメソッドとbackpropメソッドに含まれていました。 これらのメソッドは前述のアルゴリズムをそのままコードに翻訳したものです。 update_mini_batchメソッドは現在の訓練例のmini_batchについて勾配を計算し、Networkクラスの重みとバイアスを更新しています。

  class Network():
  ...
      def update_mini_batch(self, mini_batch, eta):
          """ミニバッチ1つ分に逆伝播を用いた勾配降下法を適用し、
          ニューラルネットワークの重みとバイアスを更新する。
          "mini_batch"はタプル"(x, y)"のリストで"、
          eta"は学習率。"""
          nabla_b = [np.zeros(b.shape) for b in self.biases]
          nabla_w = [np.zeros(w.shape) for w in self.weights]
          for x, y in mini_batch:
              delta_nabla_b, delta_nabla_w = self.backprop(x, y)
              nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
              nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
          self.weights = [w-(eta/len(mini_batch))*nw
                          for w, nw in zip(self.weights, nabla_w)]
          self.biases = [b-(eta/len(mini_batch))*nb
                         for b, nb in zip(self.biases, nabla_b)]
  

  ほとんどの作業はdelta_nabla_b, delta_nabla_w = self.backprop(x, y)の行で行われています。この行では、backpropメソッドを利用して偏微分$\partial C_x / \partial b^l_j$と$\partial C_x / \partial w^l_{jk}$を計算しています。 backpropメソッドは前節のアルゴリズムに従って実装されています。層への添字の振り方を、前節の説明から若干の変更しています。 この変更はPythonの特徴、具体的には負数の添字を用いてリストを後ろから数える方法を活用するために行っています（例えば、l[-3]はリストlの後ろから3番目の要素です）。 次にbackpropメソッドのコードを示します。$\sigma$関数とそのベクトル化、$\sigma$関数の導関数とそのベクトル化、及びコスト関数の微分を計算するためのヘルパー関数も併せて載せています。これらのヘルパー関数を併せて見れば、自己完結した形でコードを理解できるはずです。 もしどこかでつまづいたら 元のコードの説明（と全コード）を参照するのが良いでしょう。

  class Network():
  ...
     def backprop(self, x, y):
          """コスト関数の勾配を表すタプル"(nabla_b, nabla_w)"を返却する。
          "self.biases" and "self.weights"と同様に、
          "nabla_b"と"nabla_w"はnumpyのアレイのリストで
          各要素は各層に対応する。"""
          nabla_b = [np.zeros(b.shape) for b in self.biases]
          nabla_w = [np.zeros(w.shape) for w in self.weights]
          # 順伝播
          activation = x
          activations = [x] # 層ごとに活性を格納するリスト
          zs = [] # 層ごとにzベクトルを格納するリスト
          for b, w in zip(self.biases, self.weights):
              z = np.dot(w, activation)+b
              zs.append(z)
              activation = sigmoid_vec(z)
              activations.append(activation)
          # 逆伝播
          delta = self.cost_derivative(activations[-1], y) * \
              sigmoid_prime_vec(zs[-1])
          nabla_b[-1] = delta
          nabla_w[-1] = np.dot(delta, activations[-2].transpose())
          # 下記のループ変数lは第2章での記法と使用方法が若干異なる。
          # l = 1は最終層を、l = 2は最後から2番目の層を意味する（以下同様）。
          # 本書内での方法から番号付けのルールを変更したのは、
          # Pythonのリストでの負の添字を有効活用するためである。
          for l in xrange(2, self.num_layers):
              z = zs[-l]
              spv = sigmoid_prime_vec(z)
              delta = np.dot(self.weights[-l+1].transpose(), delta) * spv
              nabla_b[-l] = delta
              nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
          return (nabla_b, nabla_w)
  ...
      def cost_derivative(self, output_activations, y):
          """出力活性に対する偏微分\partial C_x / \partial a 
          のベクトルを返却する。"""
          return (output_activations-y)
  
  def sigmoid(z):
      """シグモイド関数"""
      return 1.0/(1.0+np.exp(-z))
  
  sigmoid_vec = np.vectorize(sigmoid)
  
  def sigmoid_prime(z):
      """シグモイド関数の導関数"""
      return sigmoid(z)*(1-sigmoid(z))
  
  sigmoid_prime_vec = np.vectorize(sigmoid_prime)
  

  問題

  • ミニバッチによる逆伝播の行列を用いた導出： 我々の確率的勾配降下法の実装ではミニバッチ内の訓練例についてループしています。しかし、逆伝播のアルゴリズムを書き換えると、ミニバッチ内の全訓練例の勾配を同時に計算するように変更できます。 単一の入力ベクトル$x$から始めるのではなく、各列がミニバッチ内のベクトルからなる行列$X = [x_1 x_2 \ldots x_m]$を用いるのが基本的なアイデアです。 この行列に重み行列を掛け、バイアス項に対応する適当な行列を足し、各要素にシグモイド関数を適用する事で順伝播をします。逆伝播も似た方法で行います このアプローチによる逆伝播アルゴリズムの擬似コードを具体的に書き下してください。 また、network.pyを行列を用いたアプローチに変更してください。 このアプローチの利点は、最近の線形代数ライブラリをフルに有効活用でき、その結果ミニバッチ内をループする場合に比べて圧倒的に高速になる点です （例えば私のノートパソコンでは、前章で考えたMNISTの分類問題で約2倍の高速化の効果が得られました）。 実際きちんと作られた逆伝播のライブラリでは、この行列のアプローチかその変種を用いています。

  逆伝播が速いアルゴリズムであるとはどういう意味か？

  どういう意味で逆伝播は速いアルゴリズムか。これに答える為に、勾配を計算する別のアプローチを考えてみましょう。 初期の時代のニューラルネットワーク研究を想像してみてください。 おそらく1950年代か60年代だと思いますが、あなたは学習への勾配降下法の適用を考えている世界で最初の研究者です！ あなたの考えがうまくいくかを確かめるには、コスト関数の勾配を計算する方法が必要です。 微積分学の知識を思い出して、勾配の計算に連鎖律が使うかを検討しています。 しかし、少しごにょごにょと計算してみると、式は複雑そうなのでがっかりしてしまいます。 そこで、別のアプローチを探します。コスト関数を重みのみの関数とみなし、$C = C(w)$と考えることにしました（バイアスについてはすぐ後で考えます）。 重みを$w_1, w_2, \ldots$と番号付けし、特定の重み$w_j$について$\partial C / \partial w_j$を計算します。 すぐに思いつくのは近似 \begin{eqnarray} \frac{\partial C}{\partial w_{j}} \approx \frac{C(w+\epsilon e_j)-C(w)}{\epsilon} \tag{46}\end{eqnarray} を利用する方法です。 ここで、$\epsilon > 0$は微小な正の数で、$e_j$は$j$方向の単位ベクトルです。 言い換えれば、$\partial C / \partial w_j$を計算する為に2つの若干異なる$w_j$でコスト$C$の値を計算し、式 (46)\begin{eqnarray} \frac{\partial C}{\partial w_{j}} \approx \frac{C(w+\epsilon e_j)-C(w)}{\epsilon} \nonumber\end{eqnarray} を適用します。 同じアイデアでバイアスについての偏微分$\partial C / \partial b$にも計算できます。

  このアプローチはよさそうに見えます。 発想がシンプルな上、実装も数行のコードで実現できとても簡単です。 連鎖律を用いて勾配を計算するアイデアよりもよっぽど有望なように思えます！

  このアプローチは有望そうですが、残念ながらこのコードを実装してみるととてつもなく遅い事がわかります。 なぜかを理解する為に、ニューラルネットワーク内に100万個の重みがあると想像してみてください。 すると、各重み$w_j$に対して$\partial C / \partial w_j$を計算するには、$C(w+\epsilon e_j)$の計算が必要です。 これには、勾配計算時に異なる値でのコスト関数計算が100万回必要で、各訓練例ごとに100万回の順伝播が必要な事を意味します。 $C(w)$の計算も必要なので、結局ニューラルネットワーク内伝播回数は100万1回です。

  逆伝播の賢い所は、たった1回の順伝播とそれに続く1回の逆伝播ですべての偏微分$\partial C / \partial w_j$を同時に計算できる点です。 逆伝播の計算コストは大雑把には順伝播と同程度です *この見積りは妥当ですが、きちんと示すには若干の分析が必要です。フォワードパスの計算コストで支配的なのは重み行列の掛け算であるのに対し、バックワードパスで支配的なのは重み行列の転置の掛け算です。これらの操作は明らかに同程度の計算コストです。。 従って、逆伝播の合計のコストはニューラルネットワーク全体への順伝播約2回分です。 (46)\begin{eqnarray} \frac{\partial C}{\partial w_{j}} \approx \frac{C(w+\epsilon e_j)-C(w)}{\epsilon} \nonumber\end{eqnarray}に基づくアプローチで必要だった100万1回の順伝播と比較してみてください！ 逆伝播は一見 (46)\begin{eqnarray} \frac{\partial C}{\partial w_{j}} \approx \frac{C(w+\epsilon e_j)-C(w)}{\epsilon} \nonumber\end{eqnarray} に基づく方法よりも複雑ですが、実際にはずっと、ずっと高速なのです。

  この高速化は1986年に始めて真価がわかり、ニューラルネットワークが解ける問題の幅を大きく広げ、その結果多くの人が次々にニューラルネットワークに押しかけました。 もちろん、逆伝播は万能薬ではありません。 特にディープニューラルネットワーク、すなわち多くの隠れ層を持つネットワークの学習への逆伝播の適用においては、1980年代後半には既に壁にぶつかっていました。現代のコンピュータや新しい賢いアイデアにより、逆伝播を用いてディープニューラルネットワークを訓練する事が可能になった事をこの本では後述します。

  逆伝播：全体像

  以前に説明したように、逆伝播には2つの謎があります。 1つはアルゴリズムが本当にやっている事は何かです。 出力から誤差が逆伝播していく様子を見てきました。 もう一歩踏み込んで、ベクトルに行列を掛ける時に何が起こっているかについてのもっと直感的な理解を得られないでしょうか。 2つ目の謎は、そもそもどうやって逆伝播を発見するかという点です。 アルゴリズムの手順に従ったり、アルゴリズムの正しさを示すを証明を追う事はできます。しかし、その事と、問題を理解しアルゴリズムをまっさらな状態から発見するのはまた別の話です。 逆伝播アルゴリズムの発見につながる妥当な論理づけは何かないでしょうか。 本節ではこれらの謎に重点を置きます。

  アルゴリズムの挙動に対する直感を養う為に、ニューラルネットワーク内の適当な重み$w^l_{jk}$に微小な変化$\Delta w^l_{jk}$を施してみましょう：

  重みの変化により、対応するニューロンの出力活性が変化します： この変化は引き続いて、次の層のすべての出力活性に変化を引き起こします： これらの変化はさらに次の層の変化を引き起こします。これを繰り返して最終層、そしてコスト関数を変化させます： コスト関数の変化$\Delta C$は重みの変化$\Delta w^l_{jk}$と次式で関連付けられます \begin{eqnarray} \Delta C \approx \frac{\partial C}{\partial w^l_{jk}} \Delta w^l_{jk}. \tag{47}\end{eqnarray} この式から、$\frac{\partial C}{\partial w^l_{jk}}$を計算するのに考えられるアプローチとして次の方法が示唆されます。すなわち、$w^l_{jk}$の微小な変化がニューラルネットワークを伝播し、その結果$C$の微小な変化を引き起こす様子を丁寧に追跡するという方法です。 もしそれができたら、伝播経路の途中にあるすべてのものを、簡単に計算できる変数で表現する事で、$\partial C / \partial w^l_{jk}$を計算できるはずです。

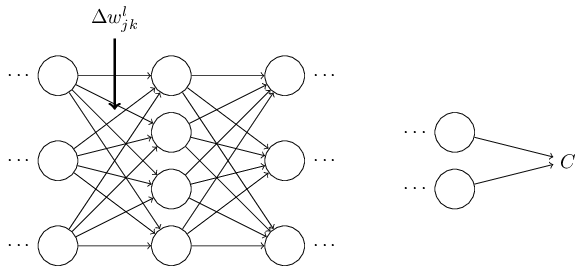
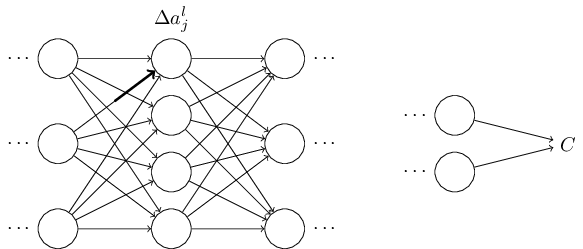
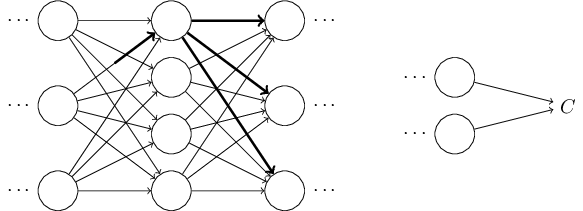
  このアイデアを実行に移してみましょう。 重みが$\Delta w^l_{jk}$だけ変化する事で$l$番目の層の$j$番目のニューロンの活性に微小な変化$\Delta a^{l}_j$が発生します。 この変化は \begin{eqnarray} \Delta a^l_j \approx \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk} で与えられます。 \tag{48}\end{eqnarray} 活性の変化$\Delta a^l_{j}$は次の層、すなわち$l+1$番目の層のすべての活性に変化を引き起こします。 私達はこれらの活性の中の1つ、例えば$a^{l+1}_q$がどのような影響を受けるかのみに注目します。

  $\Delta a^l_{j}$は次のような変化を引き起こします \begin{eqnarray} \Delta a^{l+1}_q \approx \frac{\partial a^{l+1}_q}{\partial a^l_j} \Delta a^l_j. \tag{49}\end{eqnarray} 式 (48)\begin{eqnarray} \Delta a^l_j \approx \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk} \nonumber\end{eqnarray} 内の表式をこれで置き換えると、 \begin{eqnarray} \Delta a^{l+1}_q \approx \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk} \tag{50}\end{eqnarray} が得られます。 もちろん今度は$\Delta a^{l+1}_q$が、次の層の活性に変化を引き起こします。 実際には、$w^l_{jk}$から$C$までのパスのうちの1つを考えると、このパスでは活性のそれぞれの変化が次の活性の変化を引き起こし、最終的に出力でのコストの変化を引き起こしています。 もしこのパスが$a^l_j, a^{l+1}_q, \ldots, a^{L-1}_n, a^L_m$を通るとしたら、得られる表式は \begin{eqnarray} \Delta C \approx \frac{\partial C}{\partial a^L_m} \frac{\partial a^L_m}{\partial a^{L-1}_n} \frac{\partial a^{L-1}_n}{\partial a^{L-2}_p} \ldots \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk} \tag{51}\end{eqnarray} となります。すなわち、ニューロンを通過するごとに$\partial a / \partial a$の形の項が追加され、最後に$\partial C/\partial a^L_m$の項が付け加わります。 この値は$C$の変化のうち、特定のパス内にある活性の変化に由来するものです。 $w^l_{jk}$の変化を伝播しコストに影響を与えるパスは他にもたくさんあり、この式はその中の1つしか考慮していません。 $C$の変化の合計を計算するには、最初の重みと最後のコストの間で取りうる全てのパスについて和を取れば良いです。すなわち、 \begin{eqnarray} \Delta C \approx \sum_{mnp\ldots q} \frac{\partial C}{\partial a^L_m} \frac{\partial a^L_m}{\partial a^{L-1}_n} \frac{\partial a^{L-1}_n}{\partial a^{L-2}_p} \ldots \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk}, \tag{52}\end{eqnarray} ここで、和はパスを通る中間ニューロンの選び方として考えられる全体について足し合わせます。 (47)\begin{eqnarray} \Delta C \approx \frac{\partial C}{\partial w^l_{jk}} \Delta w^l_{jk} \nonumber\end{eqnarray} と比較すると、 \begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = \sum_{mnp\ldots q} \frac{\partial C}{\partial a^L_m} \frac{\partial a^L_m}{\partial a^{L-1}_n} \frac{\partial a^{L-1}_n}{\partial a^{L-2}_p} \ldots \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \tag{53}\end{eqnarray} とわかります。 式(53)\begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = \sum_{mnp\ldots q} \frac{\partial C}{\partial a^L_m} \frac{\partial a^L_m}{\partial a^{L-1}_n} \frac{\partial a^{L-1}_n}{\partial a^{L-2}_p} \ldots \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \nonumber\end{eqnarray} は一見すると複雑そうに見えます。 しかし、これには直感的な良い解釈があります。 私達は今、ニューラルネットワーク内の重みに関する$C$の変化率を計算しています。 ニューラルネットワーク内の2つのニューロンを繋ぐ全ての枝に対して、変化率の因子が付随している事がこの式から分かります。その因子は一方のニューロンの活性に関する、もう一端のニューロンの活性の偏微分です。 ただし、先頭の重みから第1層目のニューロンに接続している枝には始点にニューロンが接続していないですが、この枝に対する変化率の因子は$\partial a^{l}_j / \partial w^l_{jk}$です。 パスに対する変化率の因子は、単純にパス内に含まれる変化率の因子を全て掛けたものとします。 そして、 $\partial C / \partial w^l_{jk}$に対する変化率の合計は最初の重みから最後のコストへ向かう全てのパスについての変化率の因子を足しあわせたものです。 下図では1つのパスについてこの手順を図示しています。

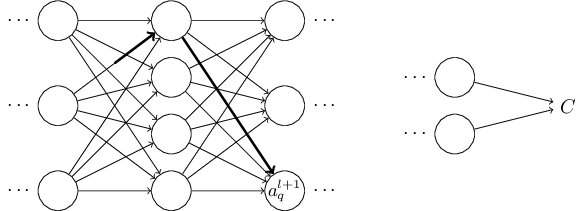
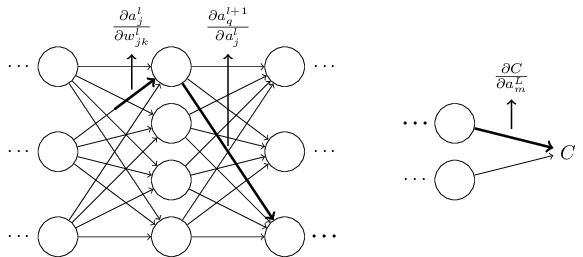
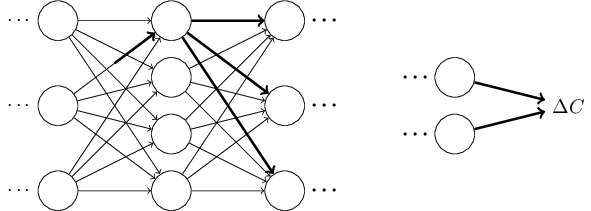
  これまでの議論は、ニューラルネットワーク内の重みを摂動させた時に何が起こっているかを発見的に考察する方法でした。 この方向で議論をさらに進める方法を簡単に紹介します。 まず、式 (53)\begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = \sum_{mnp\ldots q} \frac{\partial C}{\partial a^L_m} \frac{\partial a^L_m}{\partial a^{L-1}_n} \frac{\partial a^{L-1}_n}{\partial a^{L-2}_p} \ldots \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \nonumber\end{eqnarray} 内の偏微分はすべて具体的な表式を与えます。 これは若干の計算をするだけで難しくはありません。 これを行うと、添字について和を取る操作を行列操作に書き直す事ができるようになります。退屈で忍耐が必要な作業かも知れませんが、賢い洞察は必要ありません。 その後できるだけ式を簡単にしていくと、なんと最終的に得られる式は逆伝播アルゴリズムそのものです！ つまり、逆伝播アルゴリズムは全パスの変化率の因子を総和を計算する方法とみなすことができるのです。 少し別の表現をすると、逆伝播アルゴリズムは重み（とバイアス）に与えた小さな摂動がニューラルネットワークを伝播しながら出力に到達し、コストに影響を及ぼす様子を追跡する為の賢い方法だと言えます。

  ここでは上の議論には立ち入りません。議論の詳細を全て追うのは非常にややこしく、相当の注意が必要です。 もし挑戦する意欲があれば、試してみるとよいでしょう。 もしそうでなくても、以上の議論で誤差逆伝播が達成しようしている事について何かの洞察が得られる事を期待します。

  もう1つの謎、すなわち、まっさらの状態から誤差逆伝播を発見する方法についてはどうでしょうか。 確かに今私が概説したアプローチに従えば、誤差逆伝播の証明は発見できます。 しかし、残念ながらその証明はこの章の前の方で挙げた証明よりも若干長くて複雑です。 では、どのようにすればこのもっと短い（けれど不思議な）証明を発見できるでしょうか。 長い証明の詳細をすべて書きだしてみると、幾つかの明らかな簡略化が目につくはずです。それらの簡略化を行うと証明を短くできます、それをまた書き出してみます。すると再び明らかな簡略化が飛び出しますので、同じようにその簡略化を行います。 これを数回繰り返すと、本章の前の方で挙げた、短いけれども、若干わかりにくい証明が得られます* *1箇所賢い操作が必要な箇所があります。 式 (53)\begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = \sum_{mnp\ldots q} \frac{\partial C}{\partial a^L_m} \frac{\partial a^L_m}{\partial a^{L-1}_n} \frac{\partial a^{L-1}_n}{\partial a^{L-2}_p} \ldots \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \nonumber\end{eqnarray} において、中間変数は$a_q^{l+1}$のような活性です。賢いアイデアというのは、中間変数を$z^{l+1}_q$のような重みつき入力に取り替えるというものです。このアイデアを採用せず、活性$a^{l+1}_q$を使い続けると、最終的に得られる証明は若干複雑になります。。 証明がわかりにくいのは、それを構成する際に道標となるようなものが除かれてしまった為です。 私を信用してもらう必要があるのですが、本章で挙げた短い証明の起源には全くもって謎はないのです。本章で挙げた（短い）証明は、この章で紹介した（長い）証明を頑張って簡略化して得られたものです。