ニューラルネットワークに関して最も衝撃的な事実の1つは任意の関数を表現できることです。 例えば誰かから複雑で波打った関数$f(x)$を与えられたとします:
それがどんな関数であっても、考えられるすべての入力$x$に対して、 出力値が$f(x)$(もしくはその近似)であるニューラルネットワークが存在します。例えば下図のようなものです。
この結果は入力が複数の関数$f = f(x_1, \ldots, x_m)$や出力が複数の関数でも成立します。 例えば、下図は$m=3$個の入力と$n=2$個の出力を持つ関数を計算するニューラルネットワークです:
この結果はニューラルネットワークが一種の普遍性を持っている事を示しています。 計算したい関数が何であろうとも、その計算を行えるニューラルネットワークが存在することがわかっているのです。
しかも、この普遍性定理は入力層と出力層の間の中間層、 いわゆる隠れ層をたった1層しか持たないニューラルネットワークに限っても成立しています。 つまり、極めて単純なネットワーク構成でも表現力は極めて高いのです。
普遍性定理はニューラルネットワークを扱う人々の間ではよく知られています。 しかし、なぜそれが正しいのかはそれほど広くは理解されていません。 よく見られる説明の多くは極めてテクニカルです。 例えば、この結果を証明している原著論文* *Approximation by superpositions of a sigmoidal function, George Cybenko (1989). この結果は広く知られ、他にもいくつかのグループが関連した結果を証明しました。 Cybenkoの論文ではその仕事に関して多くの有益な議論がなされています。 初期の論文でその他の重要なものとして、 Multilayer feedforward networks are universal approximators, Kurt Hornik, Maxwell Stinchcombe, Halbert White (1989)があります。 この論文はストーン・ワイエルシュトラスの定理を用いて類似の結果を得ています。 では、ハーン・バナッハの定理とリースの表現定理とフーリエ解析を利用しています。 この論文の議論を追うのは数学者にとっては難しくないかもしれませんが、大多数の人にとっては簡単ではありません。 これは悲しいことです。なぜなら、ニューラルネットワークの普遍性を成り立たせている原因は、本当はシンプルで美しいものだからです。
本章では、普遍性定理のシンプルで大部分が視覚的な説明を行います。 背景にあるアイデア達を1つずつ順を追って見ていきます。 なぜニューラルネットワークが任意の関数を表現できるのかの理由、結果にある種の制限がついている事、 そしてこの結果と深いニューラルネットとの関連が理解できるようになるはずです。
本章を読むのにこの本のこれ以前の章を読む必要はありません。 その代わりに自己完結的なエッセイとして楽しめるよう構成されています。 ニューラルネットワークについて少し慣れていれば、説明を追えるはずです。 ただ、知識のギャップを埋めるのに役立つよう、以前の章へのリンクは必要に応じて示すつもりです。
普遍性に関する定理はコンピュータ科学では珍しくなく、それらが驚くべき定理である事をしばしば忘れてしまいます。 しかし、任意の関数を計算できるのは本当に著しい性質であることは今一度思い起こす価値のあることです。 あなたが思いつく処理は大抵どれも関数の計算と思うことができます。 例えば、音楽の短いサンプルだけを聞いて曲名を当てる問題を考えてみてください。 これも、一種の関数の構成であると考える事ができます。 または、中国語の文章を英語に翻訳する問題を考えてみてください。 やはり、これも関数の構成だと考える事ができます* 実際には1つの文章にはたくさんの妥当な訳し方があるので、多くの考えられる関数のうちの1つを構成している事になります。。 もしくは、mp4形式の映画ファイルからその映画の物語のプロットを作成する問題を考えてみてください。 これも、一種の関数構成と考える事ができます* 先程の翻訳の場合と同様ですが、妥当な関数として様々なものが考えられます。。 普遍性定理は、ニューラルネットワークがこれらやそれ以外の様々な処理を原理的にはできることを示しています。
もちろん、例えば中国語の文章を英語に翻訳するニューラルネットワークの存在が分かることは、 そのようなニューラルネットワークを構成したり、ネットワークがその性質を持つか判定する良い方法がわかることを意味しません。 ブーリアン回路のようなモデルに対する古典的な普遍性定理にもこの制限は適用されます。 しかし、この本の前の章で見てきたように、ニューラルネットワークには関数を学習する強力なアルゴリズムがあります。 学習アルゴリズムと普遍性の組み合わせは魅力的です。 ここまで、この本では学習アルゴリズムに焦点を置いてきました。本章では、普遍性とそれが意味する所に焦点を置きます。
2つの注意点
普遍性定理が何故正しいかを説明する前に、「ニューラルネットワークが任意の関数を計算できる」という砕けた表現について2つの注意点を挙げたいと思います。
まず、この表現はニューラルネットワークは任意の関数を完全に計算できる事を意味するのではありません。 そうではなく、好きなだけ近い近似関数を得られるという意味です。 隠れ層のニューロンを増やすことで、近似の精度を上げることができます。 例えば、前にある関数$f(x)$を3つの隠れニューロンを用いて計算するニューラルネットワークを説明しました。 大抵の関数については3個の隠れニューロンでは、精度の低い近似しか得られません。 隠れニューロンの数を(例えば5個に)増やす事で、より良い近似が得られます。
そして、隠れニューロンをさらに増やす事で、さらに近似を良くできます。
ステートメントをより正確にする為に、私達が計算したい関数$f(x)$と希望の精度$\epsilon > 0$が与えられたとします。 十分な数の隠れニューロンを用いる事で、出力$g(x)$が$|g(x) - f(x) < \epsilon|$を任意の入力$x$に対して満たすニューラルネットワークを常に見つけられることを普遍性定理は保証しています。 言い換えれば、希望の精度の範囲内で考えられるすべての入力に対して良い近似であることを示しているのです。
2つ目の注意点は、この方法で近似できる関数のクラスは連続関数であるという点です。 もし関数が不連続、すなわち急激なジャンプが突然発生する場合、ニューラルネットワークを用いた近似は一般的には不可能です。 これは驚くべき事ではありません。というのも、私達のニューラルネットワークが計算できるのは入力に対して連続な関数だからです。 しかし、計算したい関数が不連続でも、連続関数による近似で十分な場合もあります。その場合には、ニューラルネットを利用できます。 通常はこの制限は重大なものではありません。
まとめると、普遍性定理のより正確なステートメントは、「隠れ層を1つ持つニューラルネットワークを用いて任意の連続関数を任意の精度で近似できる」となります。 本章では隠れ層が1層ではなく2層の場合のもう少し弱いバージョンの定理を証明します。 少し証明をひねる事で本章での証明を隠れ層が1層しかない場合に適用する方法を、演習問題において簡単に説明します。
入出力が1つの場合の普遍性定理
普遍性定理の正しさを理解するために、まずは1つの入力と1つの出力を持つ関数を近似するニューラルネットワークの構成方法を理解する所から始めましょう:
この場合が普遍性の問題の中核をなします。 この特別な場合を理解すれば、入出力が多数の場合に拡張するのは容易です。
$f$を計算するニューラルネットワークの構成方法について直感を養うために、 隠れニューロンを2つ持つ隠れ層を1層持ち、出力層がニューロンを1つ持つ場合を考えます。
ニューラルネットワークを構成する各要素の挙動について感覚をつかむ為に、上の隠れニューロンに注目してみましょう。 下図で重み$w$の値をクリックしマウスを右に少しドラッグすると$w$の値が増加します。 それに応じて上の隠れニューロンの出力関数の変化する様子がわかります。
この本の前の方で学習したように、隠れニューロンで計算しているのは$\sigma(wx + b)$です。 ここで$\sigma(z) \equiv 1/(1+e^{-z})$はシグモイド関数です。 これまで、このような数式による表現を頻繁に使用してきました。 しかし、普遍性定理の証明においてはこの計算式を完全に忘れて、グラフの形を操作・観察する方がより洞察を得ることができます。 このようにすることで、単に何が起こっているかを感覚的に掴めるだけではなく、シグモイド関数以外の活性化関数に適用する普遍性定理の証明 * *厳密に言えば、私が取る視覚的なアプローチは伝統的には証明と考えられているものではありません。 しかし、視覚的なアプローチはなぜこの結果が正しいのかについて、伝統的な証明よりもより多くの洞察が得られると信じています。 そしてもちろん、この種の洞察こそが証明の背後にある真の意図なのです。 私が示す推論の中にはいくつか小さなギャップが存在します:つまり視覚的な議論を行っていて妥当だけれど厳密ではない部分です。 もしこのことが気になるようでしたら、欠けている行間を埋める事に挑戦してみてください。 しかし、なぜ普遍性定理が正しいのかを理解するという真の意図を見失わないようにしてください。 も得られます。
証明を始める前に、上図のバイアス$b$をクリックして右にドラッグすることで値を増加させてみてください。 バイアスが大きくなるに従いグラフは左に移動しますが、形は変化しないことがわかります。
次にクリック・左ドラッグをしてバイアスを減らしてみてください。 バイアスが減るにつれてグラフが右に移動しますが、やはり形は変化しない事がわかります。
次に、重みを$2$か$3$程度まで減らしてみてください。重みを減らすにつれて、曲線が広がっていくのがわかります。 曲線をフレーム内に収めるために、バイアスも変える必要があるかもしれません。
最後に重みを$w = 100$過ぎまで増やしてみてください。増加させるにつれて曲線の勾配がきつくなり、最終的にステップ関数のような形になります。 段差が$x = 0.3$あたりに来るようにバイアスを調節してみてください。 下のクリップは想定する挙動を示しています。再生ボタンを押すとビデオが再生(もしくはリプレイ)されます。

重みを増加させ、出力をステップ関数に十分近づけることで、解析を著しく単純にすることができます。 下では、重みが$w = 999$の時の上の隠れニューロンの出力を図示しています。 この図は静的で、重みなどのパラメータを変化できない事に注意してください。
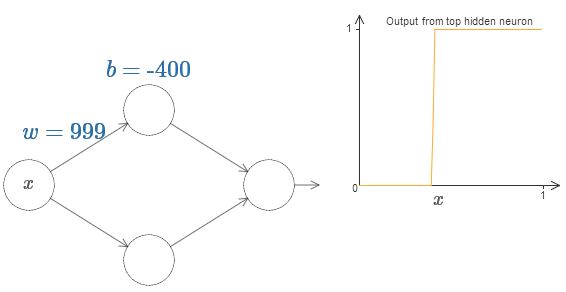
一般のシグモイド関数に比べてステップ関数で考える方が簡単です。 その理由は出力層がすべての隠れニューロンからの寄与を足しあわせるからです。 ステップ関数達の和を解析するのは簡単ですが、シグモイドの形をした曲線達を足しあわせた時に何が起こるのかを解析するのはそれに比べるとずっと難しいです。 ですので、隠れニューロンがステップ関数を出力していると仮定することでずっと簡単になります。 具体的には、重みを適当なとても大きな値に固定した後にバイアスを変化させて段差の位置を調整する事でこれを実現できます。 もちろん出力をステップ関数として扱うのは近似です。 しかしこれは十分良い近似になっているので、しばらくは厳密にステップ関数であるとして扱います。 後でこの部分に戻ってきて、この近似によるずれの影響を議論します。
ステップがあるのは$x$の値でいえばどこでしょうか? 言い換えると、段差の位置は重みや階段にどのように依存するでしょうか?
この答えに答えるために、上図の重みやバイアスを変化させてみてください(少しスクロールする必要があるかもしれません)。 段差の位置が$w$や$b$にどのように依存するかがわかりますか。 少し試してみると、段差の位置は$b$に比例し、$w$に反比例している事がわかると思います。
下図の重みとバイアスを変化させるとわかりますが、実は段差は$s = -b/w$の部分に生じます:
隠れニューロンを記述するのに段差の位置を示すパラメータ$s = -b/w$を用いると、解析を著しく単純にできます。 新しいパラメータ付けに慣れるために、下図の$s$を変化させてみてください。
前述したように、入力の重み$w$を十分大きく取り、ステップ関数が良い近似になっていることを我々は暗黙のうちに仮定しています。 バイアスを$b = -w s$と選ぶことで、1つのパラメータ$s$で特徴づけられたニューロンを前のモデルに戻す事ができます。
これまで、私達は上の隠れニューロンの出力に注目してきました。 ここでニューラルネットワーク全体の挙動を見てみましょう。 2つの隠れニューロンは段差の位置が$s_1$(上ニューロン)と$s_2$(下ニューロン)でパラメータ付けられたステップ関数を計算しているとします。 さらに、出力の重みをそれぞれ$w_1$, $w_2$とします。ニューラルネットワークは以下の通りです:
右に図示しているのは隠れ層からの重み付き出力$w_1 a_1 + w_2 a_2$です。 ここで、$a_1$と$a_2$はそれぞれ上下の隠れニューロンからの出力です* * ところで、$b$は出力ニューロンのバイアスとすれば、全ニューラルネットワークの出力は$\sigma(w_1 a_1+w_2 a_2 + b)$である事に注意してください。 もちろんこの値は今図示している隠れ層の重み付き出力とは異なります。 今私達は隠れ層からの重み付き出力に注目しているので、ニューラルネットワーク全体の出力との関連付けはその後を考えます。 これらの出力はしばしば活性(activation)と呼ばれるため、$a$で表す事にします。
上の隠れニューロンの段差地点$s_1$を増減させて、隠れ層からの重み付き出力をどのように変化させるかについて感覚を掴んでください。 特に$s_1$を$s_2$に通り越した時に何が起こるかを理解するのは有用です。 上の隠れニューロンが反応する状況から下の隠れニューロンが反応する状況に変化するために、グラフの形が変化するのがわかると思います。
同様に、下側の隠れニューロンでの段差地点$s_2$を増減させて、出力が変化する様子の感覚を掴んでください。
出力の重みをそれぞれ増減させてみてください。 それに応じてそれぞれの隠れニューロンからの寄与が拡大・縮小される事がわかります。 重みのうちの1つを$0$にするとどのようなことが起こるでしょうか?
最後に$w_1$を$0.8$、$w_2$を$-0.8$にセットしてみてください。 $s_1$から始まり$s_2$で終わる高さ$0.8$のコブ状の関数が得られます。 例えば、重み付き出力はこのような感じです:
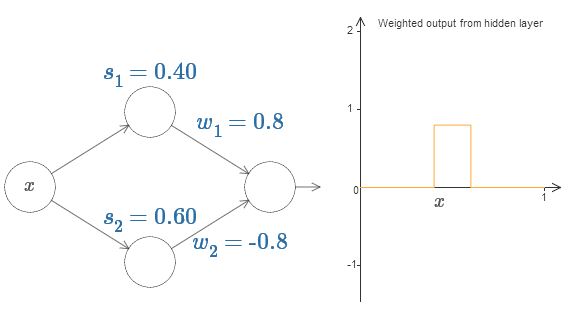
もちろん、コブの高さを任意に拡大・縮小できます。 高さを表すパラメータ$h$を導入しましょう。 煩わしさを減らす為に"$s_1 = \ldots$"や"$w_1 = \ldots$"などの式を省略します。
$h$の値を増減させてみて、コブの高さが変化する様子を見てください。 高さを負の値に変化させて何が起こるかを観察してください。 さらに、段差地点を変更してコブの形がどのように変化するかを見てください。
ところで、我々はニューロンを視覚的説明の観点からだけではなく、プログラミングの観点からも見ることができ、 ニューロンを以下の様なif-then-else構文のようもみなせる事に気づいたかもしれません。例えば次の通りです
if input >= step point:
重み付き出力に1を加える
else:
重み付き出力に0を加える
以降の説明の大部分では視覚的な観点にこだわろうと思います。 しかしこれ以降の説明を、if-then-elseの観点で考えると理解に役立つかも知れません。
このコブを作るトリックを利用し、2組の隠れニューロンのペアを1つのニューラルネットワーク内でくっつける事で、2つのコブを作る事ができます:
ここでは重みは書かず、それぞれの隠れニューロンのペアに対して$h$を書きました。 両方の$h$の値を増減させて、グラフがどのように変化するかを観察してください。 また、段差の地点を変更させることでコブを移動させてください。
より一般的には、このアイデアを利用して好きな高さで好きな数のピークを構成できます。 大きな数$N$を用いて区間$[0, 1]$を$N$個の部分区間に分割します。 そして、$N$組の隠れニューロンのペアを用いて好きな高さのピークを構成できます。 $N = 5$の場合について見てみましょう。たくさんのニューロンがあるので少し詰めて描いています。 図が複雑になってしまいすみません:省略して描けば複雑さを隠せるのですが、 ニューラルネットワークにふるまいを具体的にイメージするため、若干の複雑さは我慢する価値はあると思います。
5組の隠れニューロンのペアが見て取れると思います。 それぞれのペアの段差地点は$(0, 1/5), (1/5, 2/5), \ldots , (4/5, 5/5)$です。 これらの値は固定されており、5つの等間隔に配置されたコブを持つグラフが得られるようにします。
それぞれのニューロンペアには$h$の値が伴っています。 これらのニューロン達から出ている枝にはそれぞれ$h$、$-h$の重みが与えられています(これらは図には載せていません)。 $h$のうち一つをクリックし、左右にドラッグして値を変えてみてください。 どのように関数が変化するかを観察しましょう。 重みを変えることで、関数を設計することができるのです!
逆に、グラフをクリックし上下にドラッグして、どれかのコブの高さを変えてみてください。 高さを変化するに対応して、$h$の値が変化するのがわかると思います。 図には現れませんが、対応する出力の重み(これらの値は$+h$と$-h$です)も変化しています。
言い換えると、我々は右のグラフ内の関数を直接操作すると、それが左のニューラルネット内の$h$の値として反映されているのがわかります。 マウスのボタンを押しっぱなしにして、一方からもう一方までドラッグしてみると面白いでしょう。 関数を様々な形に引き伸ばすのに応じて、ニューラルネットワークのパラメータが変化する様子を見て取れます。
それではチャレンジの時間です。
この章の最初に私が描いた関数を思い出してください。
その時には言いませんでしたが、私が描いたのは \begin{eqnarray} f(x) = 0.2+0.4 x^2+0.3 \sin(15 x) + 0.05 \cos(50 x), \tag{106}\end{eqnarray} という関数の$x$が$0$から$1$の部分で、$y$軸は$0$から$1$の値を取っています。
見ての通りこれは簡単な関数ではありません。
これをニューラルネットワークで計算する方法を導き出してみましょう。
前述のニューラルネットワークでは、隠れニューロンからの出力の重み付き和$\sum_j w_j a_j$を解析してきました。 私達は既にこの値の調節方法を良く知っています。 しかし、前に指摘したようにこの値はニューラルネットワークの出力ではありません。 ニューラルネットワークの本来の出力は$\sigma(\sum_j w_j a_j + b)$です。 ここで、$b$は出力ニューロンのバイアス項です。 ニューラルネットワークの実際の出力を調節する方法は何かないでしょうか?
答えは、隠れ層の重み付き出力が$\sigma^{-1} \circ f(x)$を持つニューラルネットワークを設計することです。 ここで$\sigma^{-1}$は$\sigma$関数の逆関数です。 すなわち、隠れ層からの重み付き出力を以下のようにします:
もしこれができれば、ニューラルネットワーク全体での出力は$f(x)$の良い近似となります* *出力ニューロンのバイアスを$0$としている事に注意してください。。
チャレンジするのはニューラルネットワークを設計し、前述した目標関数を近似することです。 できるだけ多くのことを学ぶために、この問題を2回解いてほしいと思っています。 1回目はグラフをクリックし、それぞれのコブの高さを直接調節してください。 目標関数によくマッチする関数を得るのは比較的簡単だと感じるはずです。 調整がどの程度上手く行えているかは、 目的関数とニューラルネットワークが計算している関数との間の平均偏差で測定できます。 チャレンジするのは平均偏差を出来るだけ小さくすることです。 平均偏差を$0.40$かそれ未満に抑える事ができたらチャレンジは終了です。
1度目がうまくできたら、リセットボタンを押してコブをランダムに初期化し直してください。 2度目はグラフをクリックしたくなる気持ちを抑えて問題を解いてください。 その代わり左側の$h$の値を変更することで平均偏差を再び$0.40$かそれ未満に抑えてみてください。
これでニューラルネットワークを用いて関数$f(x)$を近似的に計算するために必要な要素が全て揃いました。 これは粗い近似ですが、隠れニューロンのペアの数を増やすことで簡単に近似精度を良くできます。
私達が見つけ出したデータをニューラルネットワークの通常のパラメータでの表現に戻すのは簡単です。 どのように行うかを簡単におさらいします。
最初の層のニューロンの重みは全て、例えば$w=1000$などの適当な大きな定数です。
隠れニューロンのバイアスは$b = -w s$です。例えば、2つ目の隠れニューロンで$s = 0.2$ならば、$b = -1000 \times 0.2 = -200$です。
最終層の重みは$h$の値によって決まります。例えば、最初の$h$について$h=$ を選んでいるので、1番上の2つの隠れニューロンでの出力側の重みは、それぞれ と です。 他の出力側の重みでも同様です。
最後に出力ニューロンでのバイアスは$0$です。
以上で、目標関数を十分良く計算できるニューラルネットワークを記述できました。 また、隠れニューロンの数を増やして近似の精度を良くする方法もわかりました。
さらに、私達は目標関数$f(x) = 0.2+0.4 x^2+0.3 \sin(15 x) + 0.05 \cos(50 x)$について特別な仮定を置いていません。 私達は$[0, 1]$から$[0, 1]$への任意の連続関数に対してこの手順を利用できます。 本質的な部分は関数のルックアップテーブルを構築するのに、1層のニューラルネットワークを用いていることです。 このアイデアを用いて、一般の場合の普遍性定理の証明を行うことできます。
多変数の場合
以上の結果を多変数の場合に拡張しましょう。 これは複雑そうに聞こえるかも知れません。 しかし、必要なアイデアは全て入力が2つの場合で理解できますので、2入力の場合に注目して考えてみましょう。
ニューラルネットワークが2入力を持つ場合に何が起こるかを考える所から始めましょう:
入力$x$, $y$とそれぞれに対応した重み$w_1$, $w_2$とバイアス$b$があります。 $w_2$の重みを$0$にした状態で1つ目の重み$w_1$とバイアス$b$をいじり、それらがニューロンの出力にどのように影響を与えるかを見てみましょう。
見ての通り、$w_2=0$とすると入力$y$の値はニューロンの出力に何の違いも生み出しません。 まるで$x$のみが入力であるかのように振る舞います。
これを踏まえて、$w_2$を0としたまま$w_1$の重みを増やして$w_1 = 100$とした時、何が起こると思いますか。 もしすぐにこの答えが分からなかったら何が起こるかを少し考えてから、それが正しいかを試してみてください。 以下の動画で何が起こるかを示しています:

以前議論したように、入力の重みが大きくなるにつれて出力はステップ関数に近づきます。 前と異なるのは今回はステップ関数が3次元である点です。 前と同様にバイアスを変更することで段差の位置を動かすことができます。 実際の段差の位置は$s_x \equiv -b / w_1$です。
段差の位置をパラメータとして、同じことをもう1度行ってみましょう:
ここで、$x$の重みは適当な大きな値(私は$w_1=1000$を用いました)とし、$w_2=0$としています。 ニューロン内の数字は段差の位置を示し、数字の上の小さな$x$の文字は段差が$x$方向である事を表しています。 もちろん、$y$の重みを大きな値(例えば$w_2=1000$)とし$x$の重みを$0$とする(すなわち$w_1=0$とする)ことで 段差を$y$方向に向けられます:
前と同様に、ニューロン内の数は段差地点です。 数字の上の小さな$y$は段差が今度は$y$方向を向いていることを表しています。 $x$と$y$それぞれの重みを明示することも出来ましたが、そうすると図が混雑してしまうので書きませんでした。 しかし、小さな文字$y$により暗に$y$の重みが大きくて$x$の重みが$0$であることを示していることを忘れないで下さい。
今つくったステップ関数を用いて3次元のコブ状の関数を構成できます。 そのためには、$x$方向のステップ関数を計算する2つのニューロンを用意し、それらのステップ関数をそれぞれ重み$h$と$-h$で結合すればよいです。 ここで$h$は作りたいコブの高さです。 以上の内容が下図に表されています。
高さ$h$の値を変更してみて、それがネットワークの重みとどのように関係しているかを観察してみてください。 また、$h$の値により右のコブ状の関数の高さがどのように変化するかを見てください。
さらに、上の隠れニューロンによって決められている段差地点を$0.30$から変更してください。 コブの形がどのように変化するかを見てみましょう。 下の隠れニューロンによって決められる段差地点を$0.70$から変えた時に何が起こるでしょうか?
私達は$x$方向にコブ状の関数を作る方法を見つけました。 もちろん、$y$方向のステップ関数を用いることで$y$方向のコブ状の関数を簡単に作れます。 そうするには、入力$y$の重みを大きくして入力$x$の重みを$0$にすればよい事を思い出してください。 下図が結果です:
これは先程のネットワークとほとんど同じものです! 図中に示した中で唯一変更しているのは、隠れニューロン内の小さな文字を$y$にした点だけです。 これは、今作っているのが$x$方向ではなく$y$方向のステップ関数であることを思い出すためのものです。 つまり入力$y$はとても大きくて$x$は$0$であり逆ではありません。 前と同様に図が煩雑にならないようにこの事は明示しませんでした。
共に高さが$h$である$x$方向と$y$方向の2つのコブ状の関数を足しあわせた時に、何が起こるかを考えてみましょう:
図を簡単にするために、重み$0$の枝は図から取り除きました。 この図ではどちらの方向のコブ状の関数を計算しているかを忘れないように隠れニューロン内の$x$と$y$の小さな文字は残しておきました。 しかし、コブの方向は入力変数からわかるので今後はこれらの文字も取り除きます。
パラメータ$h$を変化させてみてください。見ての通りこれにより出力の重みが変化し、$x$と$y$両方のコブ状の関数の高さも変化します。
これにより少し塔に似た形の関数を構成することが出来ました:
もし、このような塔状の関数を構成できれば、様々な位置にある様々な高さの塔を足しあわせることで任意の関数を近似できます:
もちろん、我々はこのような塔状の関数を構成する方法をまだ見出していません。 私達が実際に構成できているのは中央に高さ$2h$の塔がありそれを高さ$h$の台地が囲むような関数です。
ところが、私達はここから塔状の関数を構成できるのです。 ニューロンをif-then-else構文の形の関数を用いたことを思い出してください。
if input >= threshold:
1を出力
else:
0を出力
これは1入力しかないニューロンについてのものでした。 今欲しいのは同様のアイデアを複数の隠れニューロン集合からの出力をまとめた値に対して適用したものです:
if 隠れニューロン集合からの出力をまとめた値 >= threshold:
1を出力
else:
0を出力
thresholdを適切に、例えば台地の高さと中央の塔の高さに挟まれている$3h/2$のように、設定すると、 塔が立った状態で残したまま、台地を高さ$0$に潰すことができます。
これをどのように行っているかわかりますか? 理解するために次のニューラルネットワークで実験してみましょう。 今回は隠れ層からの重み付き出力ではなく、ニューラルネットワーク全体の出力を図示していることに気をつけてください。 つまり、隠れ層からの重み付き出力にバイアス項を加え、シグマ関数を適用しています。 塔を作るための$h$と$b$の値を見つけられますか。 若干トリッキーなので、しばらく考えてそれでもわからなかったら次の2つのヒントを見てください: (1) 出力ニューロンが適切なif-then-elseの挙動を示すためには、入力の重み(全ての$h$と$-h$)が大きな値でなければなりません。 (2) $b$の値はif-then-elseの閾値を決定します。
初期パラメータでは、出力は前の図での塔と台地を潰したような形をしています。 望みの塔状の関数を作るには、まずパラメータ$h$の値を十分に大きくしてください。 そうすると、関数をif-then-elseの形の閾値で切るような形にすることが出来ます。 次に、$b\approx -3h/2$として適切な閾値を設定してください。 実際にやってみてどのようになるかを確かめてください!
下の動画は$h=10$とした場合の様子です:

このような比較的小さな値の$h$でも、かなり良い塔状の関数を作る事ができます。 もちろん$h$をさらに大きくしつつ$b=-3h/2$を保つことで、この関数の形をいくらでも良くすることができます。
今度は、2つの塔状の関数を表現するために、2つのネットワークをくっつけてみましょう。 それぞれの部分ネットワークの役割を明確にするために、下図ではそれぞれを別の箱に入れました。 それぞれの箱はこれまでのテクニックを用いて塔状の関数を計算しています。 右側のグラフは2層目の隠れ層からの重み付き出力、すなわち、2つの塔状の関数の重み付きの重ねあわせを表しています。
特に、最終層の重みを変える事で、出力される塔の高さを変えることができます。
同じアイデアで好きな数の塔を計算することができます。さらにそれぞれの塔は好きな幅で好きな高さにすることもできます。 従って2つ目の隠れ層の出力はどんな2変数関数も近似できることがわかります:
特に、2つ目の隠れ層の重み付き和を$\sigma^{-1} \circ f$の良い近似にする事で、 ニューラルネットワーク全体の出力を好きな関数$f$の良い近似とする事ができます。
2変数関数以上の関数ではどうでしょうか?
3つの変数$x_1, x_2, x_3$を考えてみましょう。 次のニューラルネットワークは4次元空間の中の塔状の関数を表現する事ができます。
ここで、$x_1, x_2, x_3$はネットワークの入力を表します。 $s_1, t_1$等でニューロンの段差の点を表します。 すなわち、最初の層の全ての重みを大きくし、バイアスを段差点が$s_1, t_1, s_2, \ldots$となるようにセットします。 2つ目の層の重みは交互に$+h$と$-h$とします。ここで$h$は適当な大きな値です。さらに出力のバイアスを$-5h/2$とします。
「$x_1$が$s_1$と$t_1$の間にある」「$x_2$が$s_2$と$t_2$の間にある」「$x_3$が$s_3$と$t_3$の間にある」の3つの条件が満たされると、 このネットワークは$1$を出力します。それ以外の場合には$0$を出力します。 すなわち、この関数は入力空間の微小な領域では$1$を出力しそれ以外では$0$を出力する一種の塔状の関数を表しています。
このようなネットワークをたくさんつなげる事で、好きな数の塔を作り3変数の任意の関数を近似できます。 同様のアイデアを$m$次元の場合にも当てはめられます。 唯一変更しなければならない点は、台地の高さにあわせて適切な閾値を設定するために出力のバイアスを$(-m+1/2)h$とする点のみです。
これで、ニューラルネットワークを用いて実数値の多変数関数を近似する方法がわかりました。 それでは、ベクトル値関数$f(x_1, \ldots, x_m) \in R^n$の場合はどうでしょうか? もちろん、このような関数は$n$個の独立した実数値関数$f^1(x_1,\ldots, x_m), f^2(x_1, \ldots, x_m)$とみなす事ができます。 従って、$f^1$を近似するニューラルネットワーク、$f^2$を近似する別のニューラルネットワーク・・・を構成できます。 それらを単純につなぎ合わせれば、簡単にベクトル値関数の場合にも対応することができます。
問題
- ここまで2つの隠れ層を用いて任意の関数を近似してきました。 それでは、1つの隠れ層だけを用いても近似が可能であることを証明できますか? ヒントとして、入力変数が2つしかない場合で次のことを示してください: (a) 階段上の関数は$x$や$y$方向だけではなく任意の方向にも構成できること (b) (a) での構成した関数を足し合わせて、長方形ではなく円周の形をした塔状の関数を近似できること (c) この塔状の関数を用いて任意の関数を近似できる事。 (c) を解く際に、この章で少し後に紹介するアイデアが役立つかもしれません。
シグモイド関数以外への拡張
私達はこれまでシグモイドニューロンでできたニューラルネットワークが任意の関数を計算できることを証明してきました。 シグモイドニューロンでは、入力$x_1, x_2, \ldots$から$\sigma(\sum_j w_j x_j + b)$を出力することを思い出してください。 ここで$w_j$は重み、$b$はバイアス、$\sigma$はシグモイド関数です。
それでは、これとは異なる活性化関数$s(z)$を用いるニューロンを考えたらどうなるでしょうか:
つまり、ニューロンが入力$x_1, x_2, \ldots$、重み$w_1, w_2, \ldots$、バイアス$b$から、$s(\sum_j w_j x_j + b)$を出力するとします。
シグモイド関数の時に行ったのと同様にして、この活性化関数を用いてステップ関数を作ることが出来ます。 次の図の重みを例えば$w = 100$まで増加させてみてください:
シグモイド関数の時と同様に活性化関数は縮んでいき、最終的にはステップ関数の良い近似となります。 バイアス項を変化させてみてください。すると、段差を自分が選んだ好きな位置に置けることがわかるはずです。 これにより、私達は任意の好きな関数を計算するためにこれまでと同様のトリックを使うことができるのです。
この話がうまくいくためには、$s(z)$はどのような性質を持っている必要があるでしょうか。 $s(z)$は$z \rightarrow -\infty$と$z \rightarrow \infty$でwell-definedでなければなりません。 これらの極限はステップ関数がとる2つの値です。 また、これらの2つの値は異なることも仮定する必要があります。 もしそうでなかったとすると、階段のないただの平坦なグラフになってしまいます。 $s(z)$がこの性質さえ持っていれば、それを活性化関数にもつニューロンを用いたニューラルネットワークは普遍性を持ちます。
問題
- この本の前の方で、Rectified Linear Unitと呼ばれる、別の種類のニューロンを取りあげました。 このニューロンが今説明した普遍性のための条件を満たさない理由を説明してください。 それにも関わらず、Rectifier Linear Unitによるニューラルネットワークは普遍性を持ちます。 その事の証明をしてください。
- 線形ニューロン、つまり、$s(z) = z$という活性化関数を持つニューロンを考えます。 線形ニューロンは普遍性定理の条件を満たさない事を説明してください。 また、このニューロンによるニューラルネットワークは普遍性を持たないことを示してください。
ステップ関数
これまで、我々が考えていたニューロンはステップ関数を計算できると仮定してきました。 この仮定はとてもよい近似ですが、近似でしかありません。 実際、次のグラフで示した非常に狭い「窓」において、ニューロンの出力はステップ関数とは大きく異なる振る舞いをしています:
この窓の範囲では、普遍性について私が説明してきたことは成り立っていません。
しかし、これはそれほどひどい問題ではありません。 ニューロンへの入力対する重みを十分大きくすることで、この窓を好きなだけ小さくすることが出来ます。 実際、この窓を前に示した図中での幅よりも狭くしていき、目で判別できないほどの狭さにすることができます。 ですのでおそらく私達はこの問題に気にすることはないでしょう。
ですが、この問題について何らかの対処をしておくのは悪いことではありません。
実際、この問題は簡単に解決出来ます。 入力も出力も1つしかないニューラルネットワークについてそれをみていきましょう。 もっと多くの入出力がある場合も同じアイデアが使えます。
ニューラルネットワークをある適当な関数$f$を計算するようにしたいとします。 前と同じように、ニューラルネットワークが隠れ層の重み付き出力が$\sigma^{-1} \circ f(x)$を出力するように設計してこれを実現します:
これまで説明したテクニックを用いて、隠れ層ニューロンを用いてコブ状の関数の列を作ることが出来ます。
見やすくするために窓の幅を強調しています。 これらのコブ状の関数を足し合わせれば、窓の外では$\sigma^{-1} \circ f(x)$の良い近似になることは比較的明らかでしょう。
この近似方法を用いる代わりに、目的の関数の半分、 すなわち$\sigma^{-1} \circ f(x) / 2$を近似するように隠れニューロンを調整したとします。 もちろんこれは、直前のグラフの高さを低くしたもののような形となります。
そして、もう1組の隠れニューロンのセットを用いて、同様に$\sigma^{-1} \circ f(x)/ 2$を近似します。しかし、今度は位置をコブの幅の半分だけずらした関数を用います:
これにより$\sigma^{-1} \circ f(x) / 2$の異なる近似が1つ得られました。 これらを足し合わせることで、$\sigma^{-1} \circ f(x)$全体の近似が得られます。 この関数は依然として近似がうまくできていない微小な窓を持っています。 しかし、前と比べるとその問題はずっと小さくなっています。 というのもm一方の近似関数での窓は他方では窓になっていないからです。 従ってこれらの窓において近似はおおよそ$2$倍程度良くなっています。
大きな数$M$について、$M$個の互いに重なりあった$\sigma^{-1} \circ f(x) / M $の近似関数を足し合わせることで、近似をさらに良くできます。 窓が十分狭ければ数直線上の各点は高々1個の関数の窓の内側に含まれます。 そして、重なり合っている関数の個数$M$を十分大きく取れば、得られる関数は全体を十分に近似できるものになります。
結論
ここまで行ってきた普遍性定理の説明はニューラルネットワークを用いた計算に対する現実的な処方箋ではありません! その観点ではNANDゲートに対する普遍性定理と状況は同じです。 ですのでニューラルネットの構成方法は明快で解説が追いやすくなることに注力し、構成方法の細かい部分の最適化はしませんでした。 この構成方法を更に良くするのは面白く勉強になるでしょう。
本章での結果はニューラルネットワークを構成するのに直接有用ではありませんが、 任意の関数をニューラルネットワークで計算可能かという問いを議題から外すことができる、という点では重要です。 その問いへの答えは常に「可能である」だからです。 従ってある特定の関数を計算可能かではなく、その関数を計算する良い方法は何かというのが正しい問題設定となります。
普遍性定理の証明では任意の関数を計算するのに、2層の隠れ層を用いました。 さらに、前述のように1層の隠れ層でも同様の結果が得られます。 そうするとなぜ私達が深いネットワーク、つまり隠れ層をたくさん持つネットワークに興味を持っているかを疑問に思うかもしれません。 このような深いネットワークを隠れ層が1層しかない浅いネットワークに置き換えることは出来ないでしょうか?
謝辞 Jen DoddとChris Olahにはニューラルネットワークの普遍性に関して多くの議論を行ったことを感謝します。 特にChrisには、普遍性定理の証明の中でルックアップテーブルを利用することを提案してもらいました。 本章のインタラクティブな図は Mike Bostock、 Amit Patel、 Bret Victor、 Steven Wittens などの仕事を参考にしました。
原理的にはそのような浅いネットワークへの置き替えは可能ですが、 深いネットワークを利用するのにはきちんとした現実的な理由があります。 第1章で議論した通り、 深いネットワークは階層的な構造をしています。 このことは知識の階層構造を学習するのに適しており、現実世界の問題を解くのに有用です。 もう少し具体的に言うと、画像認識などの問題に取り組む場合、個々のピクセルを認識するだけではなく、 輪郭や単純な図形から複雑で多物体からなるシーンまで、より複雑な概念を理解するのに役立ちます。 この後の章では、深いネットワークが浅いネットワークに比べてこのような知識階層を学習するのに適していることを示唆する証拠を見ていきます。 まとめると、普遍性定理からニューラルネットワークが任意の関数を計算できることがわかりました。 そして、深いネットワークは多くの現実世界の問題を解くのに有用な関数を学習するのに適していることが経験的にわかっています。
. .






