人間の視覚がどんなに不思議なものか、考えたことはありますか?次の手書き数列を読んでみてください:
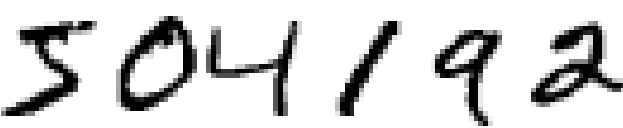
大抵の人にとってはごく簡単に504192と読めると思います。でも、脳の中で起 こっていることは簡単どころではありません。脳のふたつの半球にはそれぞれ、 一次視覚野---V1とも呼ばれる、一億四千万のニューロンと何十億ものシナ プスからなる領域が存在しています。さらに、人間の視覚に関わっている領域 はV1だけではなく、V1、V2、V3、V4、V5という一連の視覚野が、順次複雑な画 像処理に携わっています。 私たちの頭部には、数億年にわたる進化によって洗練され、視覚世界を理解するのに驚くべき適応をとげたスーパーコンピューターが内蔵されているのです。手書き数字認識が簡単なのではありません。どちらかというと、私たち人類が、目に見えるものを解釈するという作業をとても、とても得意としているのです。しかもその作業はほとんど無意識のうちに行われるのです。ですから、私たちは普段、自分の視覚系がいかに複雑な問題を解いてくれているかに、感謝を払うこともないのです。
ひとたび、さっきの手書き数字を認識するプログラムを書こうとすれば、視覚パターン認識の困難さが明らかになります。自分でやればこんなに簡単に思えることが、突然ものすごく難しくなったように感じるでしょう。数字を認識するための直感的で単純なルール---「数字の9は、上に輪があって、右下から下に向かって線が生えている形」---をアルゴリズムで表現するのはけっして単純ではないことに気づくでしょう。このようなルールを正確にプログラムとして表現しようとすれば、すぐに膨大な例外、落とし穴、特殊ケースに気づくはずです。絶望的です。
ニューラルネットワークはこのような問題に違った角度から迫ります。ニューラルネットワークの発想は、手書き数字のデータをあらかじめ沢山用意して(このようなデータを訓練例といいます)

その上で、訓練例から学習することのできるシステムを開発する、というものです。言い換えれば、ニューラルネットワークは、訓練例をもとに、数字認識のルールを自動的に推論します。さらに、訓練例を増やすほど、ニューラルネットワークは手書き文字に関する知識をより多く獲得し、精度が向上します。上図ではわずか100個の訓練例を示しましたが、何千、何万、何億個という訓練例を与えることで、よりよい手書き数字認識機を作ることができるかもしれません。
この章では、手書き数字認識を学習するニューラルネットワークを実装することを目標とします。実装するプログラムはたったの74行に収まり、しかも特別なニューラルネットワークライブラリを使うわけではありません。それでも、この短いプログラムは人手の介入なしに、96%以上の精度で数字を認識することができます。2章以降で導入する新しいアイデアを組み込めば、この性能はさらに99%を上回るまで向上します。実は、現在最高レベルの商用ニューラルネットワークは、銀行での小切手の処理や郵便局での住所認識に使われるほどの高い性能に達しています。
手書き文字認識は、ニューラルネットワーク一般について解説するうえでうってつけの題材なので、まずは手書き文字認識に話を絞ることにします。というのも、手書き文字認識というのは、決して一筋縄ではゆかない歯ごたえのある課題です。それでいて例えば極めて複雑な解法を必要とするとか、莫大な計算資源を必要とするとかの、非常に困難な課題というわけでもなく、ちょうどいい難易度の課題なのです。さらに、手書き文字認識は、深層学習といった発展的な技術の題材としても適しています。というわけで、この本では繰り返し、手書き文字認識という課題に立ち戻ることにします。この本の後のほうでは、これらのアイデアのコンピュータ視覚、音声、自然言語処理、その他の分野への応用をあつかいます。
もちろん、この章の目的がただ手書き数字を認識するプログラムを書くことだけだったなら、この章はもっと短くなったでしょう!しかし、この章では、手書き文字認識を実装する過程で、ニューラルネットワークの鍵となるアイデアをいくつも開発します。その中には、二種類の重要な人工ニューロン(パーセプトロンと、シグモイドニューロン)や、ニューラルネットワークの標準的な学習アルゴリズムである確率的勾配降下法が含まれます。本書を通じて、私は現行の手法を紹介するだけでなく*なぜ*その手法が選ばれたのかについて解説することで、あなたのニューラルネットワークにまつわる直感を鍛えてゆければと思います。おかげで、本章は流行りのトピックをただ並べた解説などよりはもずいぶん長くなってしまいますが、あなたがより深い理解に達することを思えばその価値はあると思います。とりわけ、本章を読み終わるころには、私たちは、深層学習とは何なのか、なぜ重要なのか、の理解に到達するでしょう。
パーセプトロン
ニューラルネットワークとは何か、という解説を始めるにあたり、まずはパーセプトロンと呼ばれる種類の人工ニューロンから話を始めたいと思います。 パーセプトロンは、1950年代から1960年代にかけて、 Warren McCullochと Walter Pittsらの 先行研究に触発された Frank Rosenblattによって 開発されました。 今日では、パーセプトロン以外の人工ニューロンモデルを扱うことが一般的です。 この本では、そして現代のニューラルネットワーク研究の多くでは、シグモイドニューロンと呼ばれるモデルが主に使われています。 この本でも、もうすぐシグモイドニューロンが登場します。 しかし、なぜシグモイドニューロンが今の姿をしているのか知るためにも、 まずはパーセプトロンを理解することに時間をさく価値があると言えるでしょう。
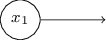
さて、パーセプトロンとは何でしょうか?パーセプトロンは複数の二進数($0$または$1$) $x_1, x_2, \ldots$ を入力にとり、ひとつの二進数($0$または$1$)を出力します。
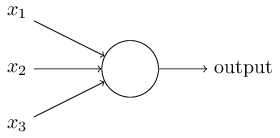
まずは基礎的となる数学モデルをご紹介しましたが、直感的にいえば、パーセプトロンとは、 複数の情報に、重みをつけながら決定をくだす機械だと言えます。例を出しましょう。 今から出すのは簡単な例ですが、あまり現実的な例ではありません。すぐに、もっと現実的な例が出てきます。
週末が近づいているとしましょう。週末には、あなたの住んでいる街で「チーズ祭り」が催されるそうです。あなたはチーズが好物で、チーズ祭りに行くかどうか決めようとしています。あなたの判断に影響を及ぼしそうなファクターは、三つあります。
- 天気はいいか?
- あなたの恋人も一緒に行きたがっているか?
- 祭りの会場は駅から近いか?(あなたは自家用車を持っていません。)
さて、あなたはチーズが大好物で、あなたの大切な人が何と言おうが、会場が駅から遠かろうが、喜んでチーズ祭りに行くつもりだとしましょう。 いっぽう、あなたは雨が何より苦手で、もし天気が悪かったら絶対に行くつもりはありません。 パーセプトロンは、このような意思決定を表現することができます。一つの方法は、 天気の条件の重みを $w_1 = 6$、他の重みを $w_2 = 2$ と $w_3 = 2$ にすることです。 $w_1$の値が大きいことは、あなたにとって天気がとても重要であること---恋人の意思や駅からの距離よりもずっとずっと重要であることを表しています。 最後に、パーセプトロンの閾値を $5$ に設定します。 以上のパラメータ設定により、パーセプトロンであなたの意思決定モデルを実装できました。このパーセプトロンは、天気が良ければ必ず$1$を出力し、天気が悪ければ必ず$0$を出力します。あなたの恋人の意思や、駅からの距離によって結論が変わることはありません。
重みと閾値とを変化させることで、様々に異なった意思決定モデルを得ることができます。 たとえば、閾値を$5$から$3$に変えましょうか。 すると、パーセプトロンが「祭りにいくべき」と判断する条件は 「天気が良い」または「会場が駅から近く、かつあなたの恋人が一緒に行きたがっている」となります。つまり、意思決定モデルが変化したのです。 閾値を下げることは、あなたが祭りに行きたがっていることを意味します。
もちろん、パーセプトロンは人間の意思決定モデルの完全なモデルというわけではありません! とはいえ、パーセプトロンは異なる種類の情報を考慮し、重みをつけたうえで判断を下す能力があることを、先ほどの例は示しています。となれば、パーセプトロンを複雑に組み合わせたネットワークなら、かなり微妙な判断も扱えそうです:
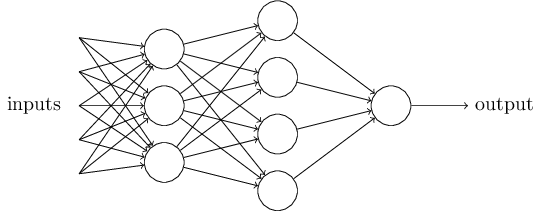
先ほどパーセプトロンを定義した時には、パーセプトロンは出力をひとつしか持たないと言いました。ところが上図のネットワークの中のパーセプトロンは、複数の出力を持つように描かれていますね。でも、あくまでもパーセプトロンの出力はひとつなんです。出力の矢印が複数あるのは、ただ、あるパーセプトロンの出力が複数のパーセプトロンへの入力として使われることを示しているにすぎません。こうすれば、一つの出力矢印を描いてから分岐させるよりも、若干見やすくなりますからね。
パーセプトロンの記法をもっと簡潔にしましょう。 パーセプトロンが$1$を出力する条件式、$\sum_j w_j x_j > \mbox{threshold}$ は何だか煩雑です。そこで、これをもっと簡単に書ける記法を導入することにします。 まず、$\sum_j w_j x_j$ という和は内積を使って、$w \cdot x \equiv \sum_j w_j x_j$と書くことにします。ここで、$w$と$x$はそれぞれ重みと入力を要素にもつベクトルです。 次に、閾値を不等式の左辺に移項し、パーセプトロンのバイアス $b \equiv-\mbox{threshold}$と呼ばれる量に置き換えます。閾値の代わりにバイアスを使うと、パーセプトロンのルールはこのように書き換えられます: \begin{eqnarray} \mbox{output} = \left\{ \begin{array}{ll} 0 & \mbox{if } w\cdot x + b \leq 0 \\ 1 & \mbox{if } w\cdot x + b > 0 \end{array} \right. \tag{2}\end{eqnarray} バイアスは、パーセプトロンが$1$を出力する傾向の高さを表す量だとみなすことができます。 あるいは、生物学の例えを使えば、バイアスとは、パーセプトロンというニューロンが発火 する傾向の高さを表すといえます。もし、あるパーセプトロンのバイアスがとても大きければ、 パーセプトロンが$1$を出力するのはとても簡単なことでしょう。逆に、パーセプトロンのバイアスが負の数なら、$1$を出力させるのは骨が折れそうです。 見てのとおり、閾値の代わりにバイアスを使うのは、パーセプトロンの表記をほんの少し変更するにすぎません。しかし、バイアスを使ったほうがもっとシンプルになる場合がのちほど出てきます。 というわけで、この本では今後、閾値ではなくバイアスを使うことにします。
ここまでの解説では、パーセプトロンを入力情報に重みをつけて判断を行う手続きとして用いてきました。パーセプトロンには他の用途もあります。それは、論理関数を計算することです。
あらゆる計算は、AND、OR、そしてNANDといった基本的な論理関数から構成されている、とみなすことができます。パーセプトロンは、こういった論理関数を表現できるのです。例えば、二つの入力をとり、どちらも重みが$-2$で、全体のバイアスが$3$であるようなパーセプトロンを考えてみましょう。図にすると、こうなります:
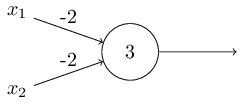
NANDゲートを実装していることになります!
NAND ゲートの例から、パーセプトロンが単純な論理関数を計算できることが分かります。それどころか、パーセプトロンのネットワークさえあれば任意の論理関数を計算できることまで分かるのです。なぜなら NAND ゲートは論理計算において万能だからです。万能だ、とは、 NAND ゲートさえあればどんな計算でも構成できる、という意味です。たとえば、 NAND ゲートを使って1ビットの二進数どうしを加算する回路を作ることができます。
入力の二進数を $x_1$ と $x_2$ としましょう。これらの和を表現するには二進数で二桁が必要です。一桁目は入力の排他的論理和 $x_1 \oplus x_2$ になります。二桁目は $x_1$ と $x_2$ がともに $1$の場合だけ $1$ になる繰り上がりビットです。繰り上がりビットは、ただの論理積 $x_1$ AND $x_2$ である、ともいえます。
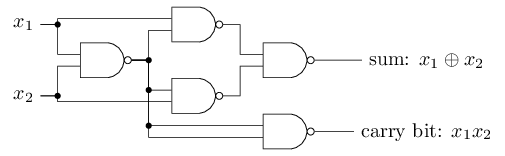
NANDゲートをすべて、重み
$-2$の入力を二つ持ち、バイアスが$3$であるパーセプトロンに置き換えます。
この置き換えを施すと、以下のようなネットワークができます。
ただし、右下にあったNANDゲートに対応するパーセプトロンだけは、矢印が見やすいように少し動かしてあります:
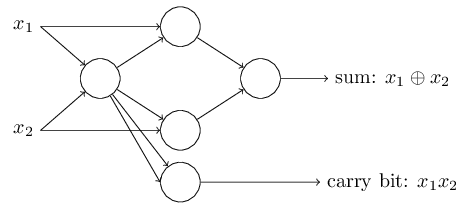
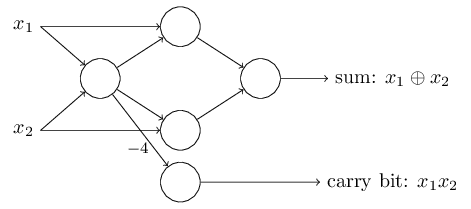
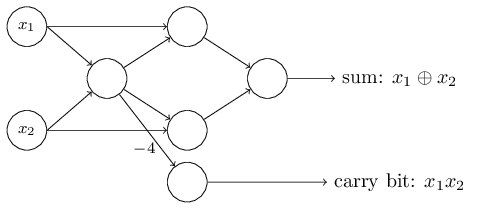
加算機の例は、パーセプトロンのネットワークがNANDゲートを多数含む回路をシミュレートすることに使える、ということの実例でした。
そして、NANDゲートの万能性(それさえあればどんな関数でも計算できるという性質)から、パーセプトロンもまた万能である、ということが導けます。
パーセプトロンが計算論的万能性を持つということは、心強いと同時に残念な事実です。
心強い、というのは、パーセプトロンが他のどの計算装置にも負けない強力さを持つことを、この事実は教えてくれるからです。残念だ、というのは、パーセプトロンはNANDゲートの亜種、四角い車輪の再発明に過ぎない、と感じられるからです。これでは、とても大したニュースとはいえません!
ところが、現実はそれほど残念ではないのです。なぜなら我々は、ニューラルネットワークの重みとバイアスを自動的に最適化するような、学習アルゴリズムを開発することができるからです。
この最適化は、プログラマの直接介入なしに、外部刺激に反応して勝手に起こるものです。
これらの学習アルゴリズムのおかげで、人工ニューロンは、従来の論理ゲートとは全く異なった使い方ができます。NANDゲートや他の種類の論理ゲートはすべて手動で配線してやる必要があったのに対し、ニューラルネットワークは問題の解き方を自発的に学習してくれます。ときには、従来型の回路を設計するのが非常に難しいような問題に対してさえも。
シグモイドニューロン
学習アルゴリズムとは大変すばらしい。でも、ニューラルネットワークに対してそのようなアルゴリズムをどう設計すればいいのでしょう? かりに、私たちがある種の問題をパーセプトロンのネットワークを使って解こうとしている、としましょう。例えば、入力は手書き文字のスキャン画像の生ピクセルデータである、とか。そして、ニューラルネットワークには、数字を正しく分類できるよう、重みとバイアスを学習してほしいわけです。学習がどのように働くのか知るために、ネットワークの中のいくつかの重みやバイアスを少しだけ変更するとしましょう。私たちとしては、このような小さな変更に対応する、ニューラルネットワークからの出力の変化もまた小さなものであってほしいわけです。まもなく出てきますが、この性質こそが学習を可能にするのです。図示すれば、こんな感じです(もちろん、図のニューラルネットワークは手書き文字認識をするには小規模すぎます!)
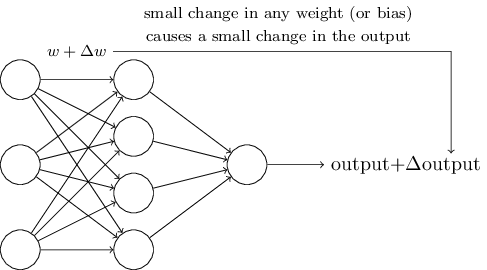
もし、重みやバイアスを微小に変化させた場合の出力の変化もまた微小である、という性質が本当に成り立っていれば、その性質をつかって、ニューラルネットワークがより自分の思ったとおりの挙動を示すように重みとバイアスを修正できます。たとえば、ニューラルネットワークがある「9」であるべき手書き文字を、間違って「8」に分類したとします。私たちは重みやバイアスに小さな変化を与えて、どうすればこのニューラルネットワークがこの画像を正しく「9」と分類する方向に近づくか探ることができます。この過程を繰り返し、重みとバイアスを変化させ続ければ、生成される結果は次第に改善されてゆくでしょう。ニューラルネットワークはこうして学習するのです。
問題は、ニューラルネットワークがパーセプトロンで構成されていたとすると、このような学習は起こらない、ということです。実際、ニューラルネットワーク内のパーセプトロンのうち、どれか1つの重みやバイアスを少し変えてやると、そのパーセプトロンの出力は、変化がないか、もしくは$0$から$1$へというようにすっかり反転してしまいます。このように出力が反転すれば、ニューラルネットワーク内の他の部分の挙動も、連動して複雑に変わっていってしまいます。 つまり、先程の手書き文字の「9」を、なんとか正しく数字の「9」に分類させることができたとしても、今度は「9」以外の全ての手書き文字に対するニューラルネットワークの挙動までもが完全に変わってしまい、その変化をコントロールすることは困難となります。 もしかしたら、この問題を回避することのできる何らかの賢い方法があるかもしれませんが、今のところ、パーセプトロンで構成されたニューラルネットワークに上手に学習させる方法は明らかになっていません。
この問題は、シグモイドニューロンと呼ばれる、新しいタイプの人工ニューロンを導入することによって克服することができます。 シグモイドニューロンはパーセプトロンと似ていますが、シグモイドニューロンの重みやバイアスに微小な変化を与えたとき、それに応じて生じる出力の変化も微小なものに留まるように調整されています。このことは、シグモイドニューロンで構成されているニューラルネットワークの学習を可能にする、決定的な違いとなります。
よし、それではシグモイドニューロンをご説明しましょう。シグモイドニューロンは、パーセプトロンと同じような見た目で描くことにします:
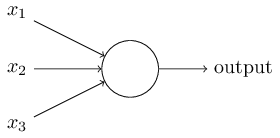
一見すると、シグモイドニューロンはパーセプトロンとは大きく異なるように見えます。シグモイド関数の数式は、こういった表現方法に慣れていない人にとっては、理解困難で近づき難く感じられるかもしれません。 しかし実は、パーセプトロンとシグモイドニューロンには多くの共通点があり、シグモイド関数が代数形式で表現されていることは、真の理解の妨げになるどころか、技術的な細部を伝えてくれるものとなるでしょう。
パーセプトロンとの共通点を理解するために、$z \equiv w \cdot x + b$を大きな正の数としてみましょう。 このとき、$e^{-z} \approx 0$、つまり$\sigma(z) \approx 1$となります。 言い換えると、$z = w \cdot x+b$を大きな数であるとき、シグモイドニューロンの出力はほぼ$1$となり、パーセプトロンと同じになります。 逆に、$z = w \cdot x+b$は大きな負の数とします。そのとき$e^{-z} \rightarrow \infty$であり、$\sigma(z) \approx 0$になります。 つまり、$z = w \cdot x +b$が大きな負の数となるときも、シグモイドニューロンはパーセプトロンとほぼ同じ動きをします。 ただし、$w \cdot x+b$がそこまで大きな数でない場合はパーセプトロンと同じにはなりません。$\sigma$についてですが、 代数的視点から私達はこれをどう理解すればいいのでしょうか? 実は、$\sigma$がなんであるかはそこまで重要ではありません。重要なのはどういう形のグラフになるかです。これがそのグラフの形です。
このグラフはステップ関数のなめらか版です:
もし$\sigma$が実際にステップ関数であれば、シグモイドニューロンはパーセプトロンと等しくなります。 これは、$w\cdot x+b$が負か正かになることで出力が$1$か$0$となるからです。 実は、$w \cdot x +b = 0$のとき、ステップ関数の出力が$1$に対して、パーセプトロンの出力は$0$です。 正確に言うと、この一点においてステップ関数を変更する必要があります。しかし、わかりますよね。 本当の$\sigma$関数を使うことによって、上にあるように、なめらかなパーセプトロンになります。 確かに、$\sigma$関数の滑らかさは重大な事実ですが、本質ではありません。 $\sigma$の滑らかさは、重みについて$\Delta w_j$、バイアスについて$\Delta b$の小さな変化は、ニューロンの出力について$\Delta \mbox{output}$の小さな変化を生み出す、ということを意味しています。 実際下記の計算から、$\Delta \mbox{output}$は大体上手くいっているとわかります。 \begin{eqnarray} \Delta \mbox{output} \approx \sum_j \frac{\partial \, \mbox{output}}{\partial w_j} \Delta w_j + \frac{\partial \, \mbox{output}}{\partial b} \Delta b, \tag{5}\end{eqnarray} ここではsumは全ての重み$w_j$の和、$\partial \, \mbox{output} / \partial w_j$と$\partial \, \mbox{output} /\partial b$は$\mbox{output}$の偏微分を表し、それぞれに$w_j$と$b$をかけています。 偏微分について知らなくてもパニックにならないでください!この記法は複雑に見えますが、全ての偏微分は実は非常にシンプルなことを表現しています(そしてとてもいいことです)。つまり、$\Delta \mbox{output}$は重みとバイアスにおいて、$\Delta w_j$と$\Delta b$の変化に対して線形である、と言っているのです。 この線形性は、欲しいoutputがどんな小さな変化でも、重みとバイアスを小さく変化させることで簡単に得られることを示しています。 このことから、シグモイドニューロンはパーセプトロンとほぼ同等な動きをするにも関わらず、より容易に重みとバイアスの変化がoutputを変化させるかがわかります。
もし、本当に重要であるのが$\sigma$のグラフの形であり、その式自体でないのであれば、なぜ$\sigma$で使われるような特定の等式を使うのでしょうか (3)? 実際、後に時折別のアクティベーション関数$f(\cdot)$を使った$f(w \cdot x + b)$の出力を持つニューロンを考えます。 別のアクティベーション関数を使った時の主な違いは、等式における偏微分の特定の値です。 (5) 後々これらの偏微分を計算するとき、$\sigma$を使うことで代数的考えが楽になります。これは単に、指数関数の値は指数によって決まるからです。 とにかく、$\sigma$はニューラルネットでよく使われており、この本で最もよく使うアクティベーション関数です。
シグモイドニューロンからの出力をどう変換すべきでしょうか?明らかなことですが、パーセプトロンとシグモイドニューロンの大きな違いの一つは、シグモイドニューロンの出力がちょうど$0$または$1$ではないことです。 シグモイドニューロンは$0$から$1$の間のあらゆる実数を出力することが出来ます。例えば$0.173\ldots$ や $0.689\ldots$ は正当な出力と言えます。 このことはとても有用となりえます。例えば、出力値をニューラルネットワークに対する入力画像のピクセル平均色度合いとして表したい時です。 しかし、時々厄介なものともなりえます。 ネットワークからの出力を「入力画像が9」もしくは「入力画像が9でない」として示したいとします。 明らかに、最も簡単は方法はパーセプトロンのように出力を$0$もしくは$1$とすることです。 しかし実際のところ、この例を扱うためにルールを設定することが出来ます。例えば、0.5より大きな出力は"9"とみなし、0.5以下の出力は"9ではない"とみなす方法です。 混乱がないように、このようなルールを使うときは常に明示することにします。
Exercises
- シグモイドニューロンのシミュレーション パート I $\mbox{}$
今、あるパーセプトロンのネットワークのすべての重みとバイアスをとって、 ある正の定数$c > 0$で定数倍するとします。 このときネットワークの振る舞いは変わらないことを示してみてください。 - シグモイドニューロンのシミュレーション パート II $\mbox{}$
先ほどの問題(=パーセプトロンのネットワーク)と同じ設定で考えます。 さらにパーセプトロンネットワークへの入力全体はすでに選ばれているとします。 ここで、入力の具体的な値は必要ではなく、入力値が固定されてさえいれば問題ありません。 重みとバイアスは、ネットワーク内の任意のパーセプトロンにおいて、 入力$x$に対し$w \cdot x + b \neq 0$を満たしているものとします。 今、ネットワーク内の全てのパーセプトロンをシグモイドニューロンで置き換え、 重みとバイアスを全て$c > 0$となるような正の数で定数倍するとします。 このとき$c \rightarrow \infty$の極限において、 このシグモイドニューロンのネットワークはパーセプトロンの場合と全く同じように振る舞うことを示して下さい。 またパーセプトロンのうちの1つが$w \cdot x + b = 0$を満たす場合には この性質は成り立ちません。なぜでしょうか?
ニューラルネットワークのアーキテクチャ
次の章では、手書きの数字の分類においてとても上手く働くニューラルネットワークを紹介します。その準備として、いくつかの専門用語を説明するためにニューラルネットワークのそれぞれの部分に名前をつけておきましょう。
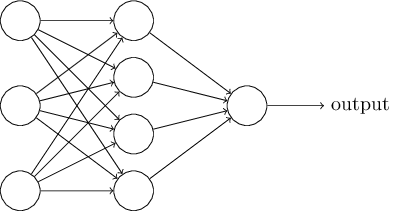
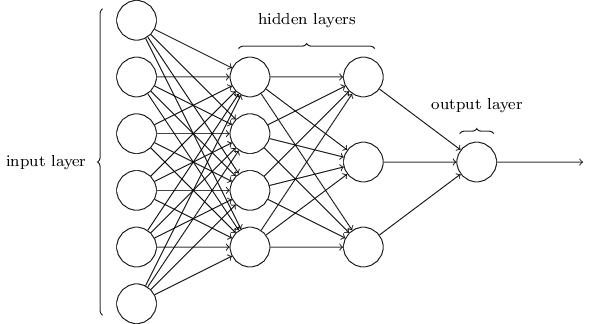
ニューラルネットワークの入出力層の設計はしばしば単純です。例えば、手書きの画像が9かそうでないかを判断したいとします。設計の自然な方法は、その画像のピクセルあたりの色の度合いを入力ニューロンにエンコードすることです。もしその画像が$64 \times 64$の白黒画像であれば、入力ニューロンの数は$4,096 = 64 \times 64$になり、色の度合いは明度を$0$から$1$の適切な値で表します。出力層は1つのニューロンからなり、出力値が$0.5$以上なら"入力画像は9である"ということを示し、$0.5$以下なら"入力画像は9ではない"ということを示します。
入出力層の設計が単純なのに対し、隠れ層の設計はかなり創造的なものになり得ます。とりわけ、隠れ層の設計の過程をいくつかの単純で大雑把な方法で行うのは不可能です。そのかわり、ニューラルネットワークの研究者らは、多くの隠れ層の設計ヒューリスティクスを開発してきました。そしてそれらは人々を解放しました。例として、これらのヒューリスティクスは学習時間と隠れ層の数とのトレードオフに折り合いをつけることができます。私たちも後に、この本の中でそのいくつかの設計に触れることになるでしょう。
これから、ある層の出力が次の層の入力になるようなニューラルネットワークについて考察してみましょう。このようなネットワークはフィードフォワードニューラルネットワーク(feedforward neural networks)と呼ばれます。これはネットワーク内にループがないということを意味しています。情報は常に前へ伝わり、後ろへは戻りません。もしループするならば、σ関数の入力はその出力に依存した状態になってしまうでしょう。そうなってはわけがわかりません。そのために私たちはそのようなループを許さないのです。
しかしながら、フィードバックループを用いることが可能な、人工ニューラルネットワークモデルも存在します。それらのモデルは再帰型ニューラルネットワーク(recurrent neural networks)と呼ばれます。これらのモデルの着想は、静止するまでの限られた時間に発火するようなニューロンをもったモデルというものです。その発火が他のニューロンを刺激し、そのニューロンもまた限られた時間の中で少し遅れて発火します。そうやってさらなる発火を引き起こし、私たちは発火の連なりを得ることができます。これらのモデルにおいてループは問題にはなりません、なぜならその出力は即時ではなく、いくぶんか遅れてその入力に影響されるからです。
再帰型ニューラルネットワークはフィードフォワードニューラルネットワークに比べてあまり影響力がありませんでした。その理由の一つは、再帰型ネットワークの学習アルゴリズムが非力だったことです。それでも再帰型ネットワークは非常に興味深いと言えます。それらはフィードフォワードネットワークに比べ、私たちの脳の働き方に近いのです。そしてフィードフォワードネットワークでは困難な問題を、再帰型ネットワークでは解くことができるという可能性は十分にあります。しかしながらこの本では、より広く使われているフィードフォワードニューラルネットワークに焦点を当てたいと思います。
手書き数字を分類する単純なネットワーク
ニューラルネットワークの定義を終えて、いよいよ手書き数字の認識に戻ります。私たちは手書き数字認識の問題を2つの下位問題にわけることができます。1つは、複数桁の数字からなる画像を、それぞれの数字からなる分かれた画像の列にすることです。例えばこの画像を、
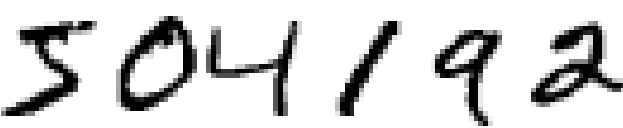
6つの分かれた画像にします。

私たち人間はこの分割問題(segmentation problem)を容易に解くことができますが、コンピュータプログラムが正確に画像を分解することは容易ではありません。一度画像を分けてしまえば、あとは個々の数字を分類するだけです。つまり上記の数字で、最初にプログラムに認識させるのは、
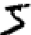
5です。
これから2つ目の問題、つまり各数字の分類問題を解くプログラムに焦点を当てます。なぜなら、この問題を解く良い方法がわかれば、1つ目の問題、つまり分割問題はそれほど難しくなくなるからです。分割問題へのアプローチは多数あります。そのひとつは、多くの異なる方法で画像を分割して、その画像の分類の結果から、それぞれの分割法を評価する方法です。すべての分割された画像で分類がうまくいけば、その分割法は高いスコアを得ます。逆にうまくいかなければそれはスコアの低い分割法となります。これは、分類でなにか問題が起これば、おそらくそれは誤った分割法を用いているからだ、というアイディアです。このアイディアやその他の派生した方法は、分割問題をうまく解くことができます。要するに私たちは、分割法に悩む代わりに、もっと面白くて難しい問題、つまり個々の手書き数字の認識問題を解くニューラルネットワークを開発していきます。
それぞれの数字を認識するために、3層のニューラルネットワークを用います。
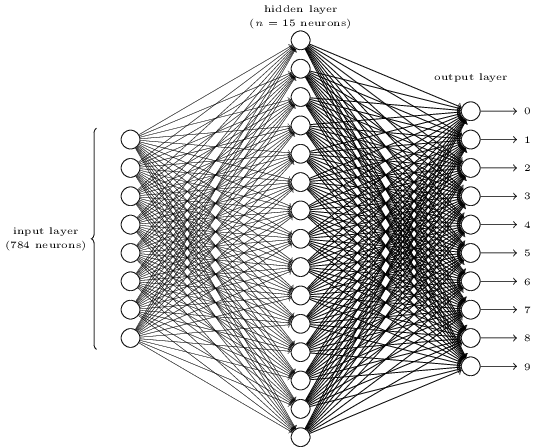
ネットワークの入力層はピクセルの値をエンコードするニューロンを持っています。次の章で論じますが、私たちが使う訓練用データは、手書き数字の$28 \times 28$ピクセルの画像です。つまり入力層は$28 \times 28 = 784$ニューロンからなるということです。簡単のため、上記の図ではニューロンの数を省略して書いています。入力ピクセルはグレースケールで、$0.0$は白を、$1.0$は黒を表し、その間の値はそれに応じた濃さのグレーを表します。
二番目の層は隠れ層です。この隠れ層のニューロンの数を$n$とし、$n$の値を変えて実験します。この例では$n = 15$ニューロンだけもつ小規模な隠れ層を表しています。
出力層は10ニューロンから構成されています。もし最初のニューロンが発火(出力 $\approx 1$)したら、それは、ネットワークがその数字を$0$だと思っていることを示しています。もし二番目のニューロンなら$1$、その他も同様です。もう少し正確に言えば、私たちは$0$から$9$の出力ニューロンをもっていて、どのニューロンが最も高く活性化するかを計算します。例えばそのニューロンが$6$だとすると、ネットワークは入力の数字が$6$であると推測していることになります。他の出力ニューロンについても同様です。
あなたは、なぜ私たちが10個の出力ニューロンを用いるか疑問に思ったでしょう。結局のところ、このネットワークのゴールは、入力の画像に対してそれがどの数字($0, 1, 2, \ldots, 9$)なのか示すことなのです。これを行うのに自然だと思われる方法は、4つの出力ニューロンを用いて、それぞれのニューロンで出力が0または1に近いかどうかに応じてバイナリの値をとることです。答えをエンコードするには4つのニューロンで十分です。なぜなら$2^4 = 16$は入力の数字の$10$より多くの値をとることができるからです。ではなぜ私たちはその代わりに10個のニューロンを用いているのでしょうか。非効率的ではないのでしょうか。その究極の正当化は経験に基づくものです。私たちはそのどちらの方法も試し、この特定の問題においては、10個の出力ニューロンをもったネットワークの方が4つのそれよりうまく学習するということがわかったのです。しかし同時に、なぜ10個の出力ニューロンを用いた方がうまくいくのかという疑問が残りました。なにか、私たちが4-出力エンコーディングの代わりに10-出力エンコーディングを用いるべきだというヒューリスティクスがあるのでしょうか。
なぜこうするのか理解するために、ニューラルネットワークが何をしているか、その原理から考えます。最初のケース、つまり$10$個の出力ニューロンを用いた場合を考察してください。最初の出力ニューロンに焦点を当ててみると、これはその数字が$0$かどうかを決めようとしていることがわかります。これは隠れ層からの情報を考量して行います。それらの隠れ層は何をしているのでしょうか。そうですね、議論のためにとりあえず、隠れ層の最初のニューロンが、下記のような画像が存在するかどうかを検出すると思ってください。

その検出は、その画像と重なった入力ピクセルに重く重み付けし、他の入力には軽い重み付けをすることで、行うことができます。同様の方法で、二番目、三番目、四番目の隠れニューロンも、下記のような画像が存在するかどうかを検出すると思ってください。

おそらくもうあなたが気付いているように、これらの4つの画像は合わせると、私たちが前に見た、数字の列の$0$の画像になります。

つまり、もしその4つ全ての隠れニューロンが発火したら、私たちはその数字が$0$であると結論づけることができます。もちろんそれだけが、その画像が$0$であると結論づく証拠ではありません。私たちは、その他の多くの方法で(例えば上記の画像の変換や僅かな歪みによって)合理的に$0$を得ることができます。しかし少なくともこの場合では入力は$0$だと結論づけて差し支えないでしょう。
ニューラルネットワークがこの方法で機能するとすれば、なぜ$10$出力ニューロンの方が$4$よりも良いのかについての尤もな説明を得ることができます。もし$4$つの出力だとすると、最初の出力ニューロンはその数字の最上位ビットが何なのか決めようとするでしょう。しかしその最上位ビットを、上に示したような単純な形状に関連づける方法はありません。数字を構成する要素の形状が出力の最上位ビットに深く関係する、という歴史的な理由は想像しがたいでしょう。
今言及したこれらのことは、すべてただのヒューリスティクスです。三層ニューラルネットワークは必ずしもこの方法、つまり私が説明した、隠れ層が単純な構成要素を検出するような方法で行う必要はありません。おそらく、巧妙な学習アルゴリズムが、$4$出力ニューロンを使うような重みの割当てを見つけるでしょう。しかし経験則的に、私が説明してきた考え方はとてもうまくいき、良いニューラルネットワークアーキテクチャを設計する上で、あなたの時間を節約することができます。
エクササイズ
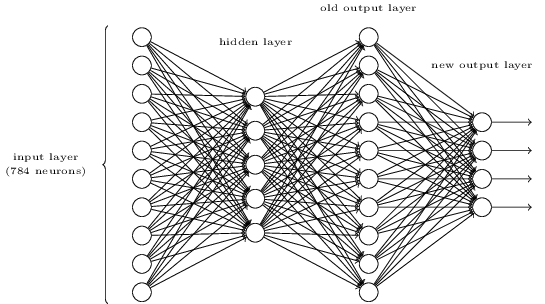
- 3層ネットワークの上にもう一つ層を追加することで、数字のビットワイズ表現を定める方法があります。追加した層は、下記の図のように、前の層からの出力を二進数の表現に変換します。新しい出力層のための重みとバイアスを見つけてください。ただし、最初の3層は、3層目(すなわち古い出力層)の正しい出力が少なくとも$0.99$で活性化し、誤った出力が$0.01$以下で活性化するようなものと仮定してください。
勾配降下法を用いた学習
今や私たちはニューラルネットワークのデザインを手に入れましたが、それはどのように数字の認識を学習することができるのでしょうか。最初に必要になるものはそれを用いて学習するための所謂トレーニングデータセットです。私たちは数万件の手書き数字スキャン画像とその正しい分類からなるMNISTデータセットを用います。MNISTという名称は、それがアメリカ国立標準技術研究所(NIST)によって収集および修正(Modify)された二つのデータセットから成り立っていることに由来しています。以下にMNISTの画像をいくつか示します。

実はご覧になられている数字はbeginning of this chapterで用いたものです。もちろん、私たちのネットワークのテストには訓練用ではないものを用います!
MNISTは二つの要素からなっています。一つ目は60,000個の訓練用の画像です。これらの画像は250人の手書きの標本からスキャンされたものであり、250人のうち半数はCensus Bureauの従業員で残り半数は高校生です。これらの画像は28×28ピクセルのグレースケールとなっています。二つ目は10,000個のテスト用画像です。これらの画像も同様に28×28ピクセルのグレースケールとなっています。これらのテストデータを使ってニューラルネットワークが数字の認識についてどれくらい学習できているかを評価します。テストの精度を良くするため、テストデータは訓練用データとは異なる250人から採取されています(既にCensus Bureauの従業員と高校生とでグループ分けされているにも関わらずです)。これによりシステムが認識できる数字を訓練中に経験していないと確信できます。
ここで訓練入力を $x$ と定義します。これで各入力 $28 \times 28 = 784$-次元ベクトルを $x$ とみなせ好都合です。ベクトルの各成分は一つのピクセルの濃淡値を表しています。ここで出力を $y = y(x)$ と定義し、この $y$ を10次元のベクトルとします。 仮に訓練用画像の$x$が$6$を示している場合 $y(x) = (0, 0, 0, 0, 0, 0, 1, 0, 0, 0)^T$ が期待されるネットワークからの出力です。 ここで$T$は転置演算子であり行ベクトルと列ベクトルを入れ替えます。
私たちが得たいもの、それは全訓練入力 $x$ について、ネットワークの出力が $y(x)$ になるべく近くなるような重みとバイアスを見つけるアルゴリズムです。この目標をどれだけ達成できたか測るためコスト関数を定義します* *しばしば 損失 関数 または 目的 関数とも呼ばれます。 私たちはこの本では一貫してコスト関数という用語を用いますが、ニューラルネットワークの論文や議論では他方の用語も頻繁に使われるので心に留めておいて下さい。: \begin{eqnarray} C(w,b) \equiv \frac{1}{2n} \sum_x \| y(x) - a\|^2. \tag{6}\end{eqnarray} ここで $w$ はネットワーク中の全ての重み、 $b$ は全バイアス、 $n$ は訓練入力の総数、 $a$ は入力が $x$ の時にネットワークから出力されるベクトル、和は全ての訓練入力 $x$ です。もちろん出力 $a$ は $w$ と $b$ そして $x$ に依存しますが表記をシンプルにするためここでは敢えて明示しません。$\| v \|$はベクトル $v$ の距離関数を示す記号です。 $C$ は2次コスト関数と呼びましょう。これはしばしば平均二乗誤差あるいは単にMSE(mean squared error)としても知られるものです。2次コスト関数の式を見てみると総和の中の全項目が非負であるため $C (w,b)$ は非負になることが分かります。また、 $C(w,b)$ が小さくなる時、すなわち $C(w,b) \approx 0$ の時は全訓練入力において $y(x)$ と出力がほぼ等しくなると分かります。つまり、$C(w,b) \approx 0$ となるような重みとバイアスを見つけられれば、私たちの訓練アルゴリズムは上手く機能した、と言えます。対照的に $C(w,b)$ が大きいとき-大多数の入力において $y(x)$ と出力が近似しない場合は上手く機能ているとは言えません。したがって、訓練アルゴリズムの狙いは重みとバイアスの関数 $C(w,b)$ の最小化だと言えます。言い換えれば可能な限りコストを小さくできる重みとバイアスの組を見つけたいのです。それを私たちは勾配降下法というアルゴリズムを使って行います。
しかし、なぜ2次コストを導出するのでしょうか?結局のところ私たちが知りたいのはどれだけの画像がネットワークによって正しく分類されたかではないでしょうか?直接分類の正解数を最大化せずに2次コストを最小化するのはなぜでしょうか?その理由は分類の正解数がネットワーク中の重みとバイアスの滑らかな関数にならないことです。重みとバイアスに小さな変更を加えても正解数が変化することがほとんどないため、コストを改善するのに重みとバイアスをどう変更したら良いか分からないのです。代わりに2次コストのような滑らかなコスト関数を用いた場合、重みとバイアスに対してどう小変更を加えればコストを改善できるのかが簡単に分かるようになります。これが2次コストの最小化を用いる理由であり、2次コストの最小化をした後ではじめて分類の精度を調べることにします。
たとえ、滑らかなコスト関数を用いたいとしても、あなたは等式(6) を使った2次コスト関数を選択する理由についてはまだ不思議に思っているかもしれません。これはずいぶんとアドホックな選 択ではないでしょうか?もし、仮に違うコスト関数を選んだ場合、最小化する重みとバイアスの組は全く異なってくるのではないでしょうか?それはもっともな心配で、後で私たちはコスト関数を再訪していくつかの修正を行うことになります。しかしながら、この2次コスト関数の等式(6)はニューラルネットワークの学習の基礎を理解するのにとても良く機能するので、今はこのまま続けることにします。
要約すると、ニューラルネットワークの訓練における私たちのゴールは2次コスト関数 $C(w, b)$ を最小化する重みとバイアスを見つけることです。これは良設定問題ですが、いまの定式化のままではたくさんの注意をそらす構造を持っています。重みとバイアスの解釈、背後に潜んでいるシグモイド関数、ネットワーク構造の選択、MNIST等があります。これらが明らかにするのは、私たちは膨大な構成の大部分を無視して単に最小化の面に集中しているということです。そこで、私たちはコスト関数の詳細な式やニューラルネットワークとのつながり、その他諸々については一旦忘れましょう。その代わり、私たちにはたくさんの変数からなる関数がシンプルに与えられており、その関数を最小化したいと考えることにします。私たちは、このような最小化問題を解決できる勾配降下法と呼ばれるテクニックを開発するのです。その後、最小化したいニューラルネットワークの具体的な関数に戻ってきましょう。
それでは、私たちは関数 $C(v)$ を最小化しようとしているとしましょう。$C(v)$は複数の引数 $v=v_1,v_2, \ldots$ を取って実数の値を返す関数なら何でもかまいません。ここで私は、どんな関数でも良いということを強調するために $w$ と $b$ の記号を $v$ に置き換えました。もう私たちはニューラルネットワークに特化した文脈で考えているのではありません。ここで $C(v)$ を最小化するのに $C$ が二つの変数からなる関数だと考えることが効果的です。二つの変数を $v_1$ と $v_2$ と呼ぶことにしましょう。

私たちが見つけ出したいもの、それは $C$ の大域最小値です。もちろん、今ここで与えられた関数であれば、私たちはグラフを眺めて最小値を見つけられます。そういう意味では、幾分簡単すぎる関数を示してしまいました!おそらく一般的な関数 $C$ はたくさんの変数からなる複雑な関数であるためグラフを眺めるだけでは最小値を見つけられないでしょう。
この問題の一つの攻略法は、微積分を使って解析的に最小値を見つけることです。導関数の計算結果から私たちは $C$ の極値を見つけられるでしょう。運よく関数 $C$ が一つの変数、あるいは少数の変数であればおそらく上手く行きます。しかし、変数が大量にある場合は悪夢に変わるでしょう。また、ニューラルネットワークはしばしば 膨大な 変数を必要とします-もっとも巨大なニューラルネットワークのコスト関数は10億の重みとバイアスを持っており極めて複雑になります。こういった場合、微積分による最小化は機能しません!
( $C$ を二つの変数の関数で考えれば洞察があると主張した後に"変数が二つ以上の場合はどうなってしまうでしょう?"と、二つの段落の中で立場を変えて申し訳ありません。それでも、 $C$ を二つの変数の関数で考えることが効果的だという私の言うことを信じてください。最後の2段落は概観の分析を行っているのです。しばしば数学に関する名案では、複数の直観的イメージを巧みに扱い、学習する際のイメージの適切な使い分けを伴うのです。)
さて、微積分は機能しません。幸いなことに、非常に良く機能する一つのアルゴリズムを示唆する見事な例え話があります。手始めに関数が谷であるかのように想像してみましょう。上のグラフを見てボールが谷の斜面を転がり落ちていくところを想像してください。普段の経験から、ボールは最終的に谷底まで転がっていくと分かるでしょう。この考え方を関数の最小化に使えないでしょうか?私たちは(想像上の)ボールのスタート地点をランダムに選び、その後ボールが谷底へ転がっていく動きをシミュレーションするのです。おそらく、単に $C$ の導関数(あるいは二次導関数)を微分すればこのシミュレーションが行えるでしょう。これらの微分係数は、谷の局所形状やボールがどう転がるかといった私たちが知るべき全てのことを教えてくれます。
あなたは私が述べた内容に基づき、私たちが摩擦力や重力の影響等を考慮し、ニュートンの運動方程式を書き始めると思うかもしれません。実際には、ボールの転がりの例えをそう深刻に扱ったりはしません。私たちは $C$ の最小化アルゴリズムを考案しようとしているのであり、物理法則の精密なシミュレーションを開発するわけではありません。ボール目線の観点は想像力を刺激するためのものであり、思考を制限するためではありません。そういうわけで、物理学の詳細には入っていかずにシンプルな問い掛けをします:もし私たちが一日神様を任命され、物理法則を好きに決めていいことになったら、ボールにどう動くよう命令すべきでしょう?どんな運動法則を選べばボールは谷底へと転がり続けていくでしょう?
この問いをもう少し詳細化するため、 $v_1$ 方向に微小な量 $\Delta v_1$ 、 $v_2$ 方向に微小な量 $\Delta v2$ だけボールを動かした時に何が起こるか考えてみましょう。計算の結果、 $C$ は次のようになります: \begin{eqnarray} \Delta C \approx \frac{\partial C}{\partial v_1} \Delta v_1 + \frac{\partial C}{\partial v_2} \Delta v_2. \tag{7}\end{eqnarray} ここで $\Delta C$が負の値;すなわち、ボールが谷を転がり降りていくような $\Delta v_1$ と $\Delta v_2$ を選ぶ方法を見つけましょう。これを明らかにするため、 $\Delta v$ を $v$の変化のベクトルとして、 $\Delta v \equiv (\Delta v_1, \Delta v_2)^T$ と定義し、ここで $T$ は転置演算子(再掲)なので、行ベクトルと列ベクトルを入れ替えます。同様に、 $C$ の勾配についても偏導関数のベクトル $\left(\frac{\partial C}{\partial v_1}, \frac{\partial C}{\partial v_2}\right)^T$ として定義します。ここで勾配ベクトルを $\nabla C$ と記して: \begin{eqnarray} \nabla C \equiv \left( \frac{\partial C}{\partial v_1}, \frac{\partial C}{\partial v_2} \right)^T. \tag{8}\end{eqnarray} すぐに私たちは $\Delta C$ を $\Delta v$ と勾配 $\nabla C$ に書き換えるのですが、これに着手する前に、勾配のハマりやすい箇所を明らかにしておきたいと思います。 $\nabla C$ の表記に出会った時、しばしば人々は $\nabla$ の記号をどう考えて良いのか分からずに戸惑います。 $\nabla$ の正確な意味は何でしょう?実際、 $\nabla C$ が数学における一つの記号ということは自明で-上記定義のベクトル-それは二つの記号を使って表記されています。この観点で言えば $\nabla$ は" $\nabla C$ は勾配ベクトル"とあなたに教えるため旗を振る記号の一つです。更に踏み込んだ観点では $\nabla$ はそれ自体で独立した数学の構成要素(例えば微分演算子のようなもの)であると見なせもしますが、こういった観点は私たちには必要ありません。
これまでの定義から式 (7) の $\Delta C$ を次のように変形できます。 \begin{eqnarray} \Delta C \approx \nabla C \cdot \Delta v. \tag{9}\end{eqnarray} この等式は $\nabla C$ がなぜ勾配ベクトルと呼ばれるかを教えてくれます: $\nabla C$ は $C$ を変化させる $V$ の変化に関わっており、これはちょうど私たちが勾配と呼んでいるものです。しかし、本当に面白いのはこの等式が $\Delta C$ を負にする $\Delta v$ の選び方を教えてくれるということです。とりわけ、次の仮定を与えれば \begin{eqnarray} \Delta v = -\eta \nabla C, \tag{10}\end{eqnarray} $\eta$ は小さい正のパラメータ(学習率として知られるもの)です。ここで等式(9) から $\Delta C \approx -\eta \nabla C \cdot \nabla C = -\eta \|\nabla C\|^2$ となることが分かります。$\| \nabla C \|^2 \geq 0$ であることから $\Delta C \leq 0$ が成り立つため(10)の前提に従い $v$ を変更する限り $C$ は常に減少し、決して増加しないことが保証されます(勿論(9) の等式が近似する限りです)。これはまさしく私たちが求めていた特性です!そこで等式(10)を私たちの勾配降下アルゴリズムのボールの"運動の法則"と定義しましょう。つまり、私たちは等式(10)を使い $\Delta v$ の値を計算し、ボールの位置を $v$ から次のように動かすのです: \begin{eqnarray} v \rightarrow v' = v -\eta \nabla C. \tag{11}\end{eqnarray} その後、私たちは以降もこの規則を使い続けます。もし私たちがこれを続けて、何度も繰り返すと、 $C$ は減少を続け、やがては - 待望の - 大域最小値に到達します。
要約すると、勾配降下法は勾配 $\nabla C$ を計算し逆の方向へと動かすことを繰り返すことで谷の斜面へと"降下"させる方法です。これを視覚化すると以下のようになります。
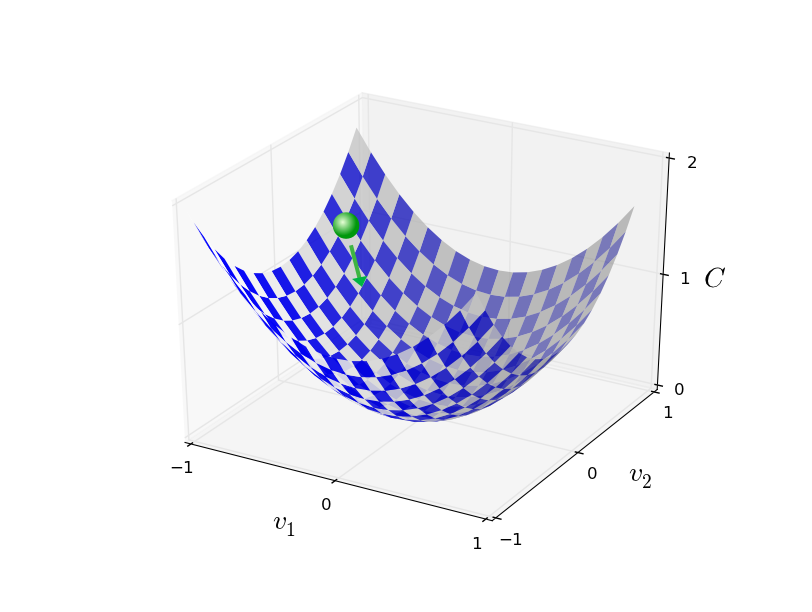
ここで留意すべきは勾配降下法の規則が現実世界の物理的な運動を再現していないということです。現実世界のボールは運動量を持っているので、斜面を転がり、(少しの間)そのまま登っていくかもしれません。その後、摩擦力によってはじめて谷を降り始めるでしょう。これに対して、私たちが $\Delta v$ を選ぶ規則は"今この瞬間だけ降りなさい"というものです。これはやはり最小値を見つけるのにとても良い規則です!
勾配降下法を正しく動作させるには十分小さな学習率 $\eta$ を選んで等式(9)をよく近似させる必要があります。さもなければ $\Delta C > 0$ となり明らかに良くありません!その一方で $\eta$ が小さすぎる場合は $\Delta v$ の変化がとても小さくなり勾配降下法の動きは非常に遅くなってしまいます。実用的な実装では、等式(9)の近似を維持できるように $\eta$ を頻繁に変更してアルゴリズムが遅くなりすぎないようにします。これがどのように行われるかは後の章で理解することにしましょう。
私は勾配降下法の $C$ がちょうど二つの変数の関数である場合を説明しました。しかし、実際には、 $C$ がもっと多くの変数の関数であっても何も問題はありません。ここで $C$ が $m$ 変数 $v_1, \ldots ,v_m$ の関数であると仮定します。この時、微小な変化 $\Delta v = (\Delta v_1, \ldots, \Delta v_m)^T$ によって持たされる $C$ の変化 $\Delta C$ は \begin{eqnarray} \Delta C \approx \nabla C \cdot \Delta v, \tag{12}\end{eqnarray} ここで勾配 $\nabla C$ のベクトルは \begin{eqnarray} \nabla C \equiv \left(\frac{\partial C}{\partial v_1}, \ldots, \frac{\partial C}{\partial v_m}\right)^T. \tag{13}\end{eqnarray} 二変数の時と同様に、次のように設定します。 \begin{eqnarray} \Delta v = -\eta \nabla C, \tag{14}\end{eqnarray} これで等式(12)の(近似)式の $\Delta C$ が負の値となるように保証されます。 $C$ が複数の変数の関数であっても、この定義を繰り返し更新して当てはめていけば、最小値への勾配に繋がる道が得られます。 \begin{eqnarray} v \rightarrow v' = v-\eta \nabla C. \tag{15}\end{eqnarray} この規則は勾配降下法の定義とみなすことができます。この規則によって$v$ の位置を繰り返し変更して関数 $C$ を最小化する 方法が分かります。この規則はどんな時でも機能する訳ではありません - しばしば間違い、勾配降下法が大域最小値の発見を妨げる場合があります。この点は、後の章でまた戻って綿密に調べます。しかし、実際には勾配降下法はほとんどの場合とても良く機能し、ニューラルネットワークのコスト関数の非常に強力な最小化手段でありネットワークの学習を助けてくれます。
実際、勾配降下法は最小値を探索する最適戦略であるとさえ感じます。私たちは $C$ を可能な限り減少する位置へと $\Delta v$ 動かそうとしていると仮定してみましょう。これは $\Delta C \approx \nabla C \cdot \Delta v$ に等しいです。ここで移動量 $\| \Delta v \| = \epsilon$ に微小な固定値 $\epsilon > 0$ という制約を与えます。言い換えれば、私たちは小刻みな固定値の動きを望んでいて、 $C$ を可能な限り減少させる移動方向を見つけようとしているのです。これは $\nabla C \cdot \Delta v$ を最小化する $\Delta v$ が $\Delta v = - \eta \nabla C$ であり $\eta = \epsilon / \|\nabla C\|$ は制約量 $\|\Delta v\| = \epsilon$ により決まるということから証明できます。つまり、勾配降下法はその瞬間に $C$ を最も減少させる方向へと小刻みに動く方法と見なすことができます。
演習
- 最後の段落の主張を証明してください。ヒント: もしあなたがまだ コーシーシュワルツの不等式について詳しくなければ、習熟することが理解に役立つでしょう。
- 私は勾配降下法の $C$ が二つの変数である場合と二つ以上の変数の関数の場合について説明しました。 $C$ がただ一つの関数の場合は何が起こるでしょう?あなたは一次元の場合の勾配降下法の動きについて幾何学的な説明が出来ますか?
より現実のボールに近い形で物理法則を摸倣する種類を含め、これまで様々な勾配降下法が研究されてきました。そういったボールを模倣する種類はいくつか長所を持っているものの、大きな欠点も持っています:二階偏微分の計算が必要であり、その計算が非常に大変なのです。なぜ計算が大変か明らかにするため、全ての二階偏微分 $\partial^2 C/ \partial v_j \partial v_k$ を計算したいと仮定してみましょう。仮に100万の変数がある時、私たちはおよそ1兆回(つまり100万の2乗)の二階微分* *実際は、1兆の半分、なぜなら $\partial^2 C/ \partial v_j \partial v_k = \partial^2 C/ \partial v_k \partial v_j$ だからです。!の計算が必要で計算量的に重くなります。そうは言っても、こういった問題を回避する手段はいくつか存在していますし、また勾配降下法の代替手段の調査は研究が盛んな分野になっています。しかし、私たちはこの本では勾配降下法(とその派生形)をニューラルネットワークの学習への主要なアプローチに使いましょう。
私たちはどうすればニューラルネットワークの学習に勾配降下法を適用できるでしょう?その考え方は等式(6)のコストを最小化する重みとバイアスの探索に勾配降下法を用いるというものです。これがどう行われるかを理解するため、変数 $v_j$ を重みとバイアスに置き換えて勾配降下法の更新規則を再定義しましょう。つまり、私たちの"位置"は要素として $w_k$ と $b_l$ を持っており、勾配ベクトル $\nabla C$ は要素として $\partial C / \partial w_k$ と $\partial C / \partial b_l$ を持っていることに一致します。これらの要素の用語で勾配降下法の更新規則を書き直すと、 \begin{eqnarray} w_k & \rightarrow & w_k' = w_k-\eta \frac{\partial C}{\partial w_k} \tag{16}\\ b_l & \rightarrow & b_l' = b_l-\eta \frac{\partial C}{\partial b_l}. \tag{17}\end{eqnarray} この更新規則を繰り返し適用することで"坂を転がり降りる"ことができ、上手くいけばコスト関数の最小値を見つけられます。言い換えれば、この規則をニューラルネットワークの学習に使うことが出来ます。
勾配降下法の規則の適用にはいくつか課題があります。この詳細は後の章で見ることにしましょう。それより今は一つの問題にだけ言及したいと思います。問題が何であるかを理解するため、等式(6)の二次コスト関数を振り返りましょう。ここでコスト関数は $C = \frac{1}{n} \sum_x C_x$ という形をしており、個々の訓練データ $C_x \equiv \frac{\|y(x)-a\|^2}{2}$ の総和になっていることが分かると思います。実際には、私たちは勾配 $\nabla C$ を計算するため、個々の訓練入力 $x$の勾配 $\nabla C_x$ を計算し、その後その平均を取って $\nabla C = \frac{1}{n} \sum_x \nabla C_x$ とします。不運にも、訓練入力の数が非常に大きい場合はとても時間が掛かり、その結果学習は非常に遅くなってしまいます。
学習の高速化に使えるアイディアの一つに確率的勾配降下法と呼ばれるものがあります。この考え方は訓練入力から無作為に抽出した小さな標本群 $\nabla C_x$ を計算して勾配 $\nabla C$ を推定するというものです。小さな標本群の平均を取ることで速やかに正しい勾配 $\nabla C$ を推定でき、勾配降下法が高速化され、ひいては学習を高速化できます。
この考え方をより正確に述べると、確率的勾配降下法は、小さい数 $m$ を無作為抽出し、訓練入力をその数だけ無作為に選ぶことで動くということです。ここでランダムに選んだ訓練入力を $X_1, X_2, \ldots, X_m$ とラベル付けし、これらをミニバッチと呼ぶことにしましょう。標本サイズ $m$ が十分大きければ $\nabla C_{X_j}$ の平均値は全ての $\nabla C_x$ の平均とほぼ同等になることが期待でき、すなわち、 \begin{eqnarray} \frac{\sum_{j=1}^m \nabla C_{X_{j}}}{m} \approx \frac{\sum_x \nabla C_x}{n} = \nabla C, \tag{18}\end{eqnarray} ここで二つ目の総和は全ての訓練データです。端と入れ替えると、 \begin{eqnarray} \nabla C \approx \frac{1}{m} \sum_{j=1}^m \nabla C_{X_{j}}, \tag{19}\end{eqnarray} ランダムに選んだミニバッチを計算して全体の勾配を推定できることが確認できます。
これを明確にニューラルネットワークの学習と紐付けるため、私たちのニューラルネットワークにおける重みとバイアスの表記 $w_k$ と $b_l$ で考えてみましょう。この時、確率的勾配降下法は無作為に選んだ訓練入力のミニバッチによって動き、それらで訓練を行います。 \begin{eqnarray} w_k & \rightarrow & w_k' = w_k-\frac{\eta}{m} \sum_j \frac{\partial C_{X_j}}{\partial w_k} \tag{20}\\ b_l & \rightarrow & b_l' = b_l-\frac{\eta}{m} \sum_j \frac{\partial C_{X_j}}{\partial b_l}, \tag{21}\end{eqnarray} 総和は現在のミニバッチにおける全ての訓練サンプル $X_j$ です。次に、私たちは別の無作為に選んだミニバッチで訓練を行います。同じように、訓練入力がなくなるまで続ければ、1回の訓練のエポック(訳注:訓練データ全体を1巡する事)が完了します。この時点で私たちは新しい訓練エポックをやり直します。
ちなみに、コスト関数とミニバッチで重みとバイアスを更新する縮尺の取り方によって、更新規則が異なってくることは注目に値します。等式(6)で私たちは全てのコスト関数を $\frac{1}{n}$ の縮尺にしました。しばしば人々は $\frac{1}{n}$ を省略し、個々の訓練例のコストの平均を取る代わりに総和を取ります。これはとりわけ訓練例の総数が事前に分かっていない場合に有効です。これは、例えば、リアルタイムに訓練データが生成されている場合に生じ得ます。そして、同じように、ミニバッチの更新規則 (20) と (21) でもしばしば総和の前にある $\frac{1}{m}$ を省略します。これは学習率 $\eta$ の縮尺の大きさを変更することに相当するので概念的には大差がありません。しかし、両者の動作の詳細な比較について気にすることは価値のあることです。
確率的勾配降下法は世論調査のように考えることができます:国民総選挙よりも世論調査を実施する方が簡単であるように、全部一括処理で実施するより小さな標本のミニバッチの方が勾配降下法の適用は簡単です。例えば、仮に私たちがMNIST等で $n = 60,000$ の訓練セットを持っておりミニバッチの大きさが(例えば) $m = 10$とすると、勾配の推定を $6,000$ 倍速く出来ます!勿論、この推定は完璧ではありません - これには統計変動があるでしょう - しかし、完璧である必要はありません:私たちが気にするのは $C$ が減少する大まかな移動方向だけなので、勾配の正確な計算は必要ありません。実際、確率的勾配降下法はニューラルネットワークの学習によく用いられている強力な手法であり、また、私たちがこの本で開発する学習テクニックにおける大部分の基礎になります。
演習
- 極端な勾配降下法は大きさ1のミニバッチを使います。つまり、与えられた一つの訓練入力 $x$ について、重みとバイアスを規則に従い更新して $w_k \rightarrow w_k' = w_k - \eta \partial C_x / \partial w_k$ と $b_l \rightarrow b_l' = b_l - \eta \partial C_x / \partial b_l$。その次に、別の訓練入力を選び、そして再びバイアスを更新します。この手続きはオンライン学習または逐次学習として知られるものです。オンライン学習は、ニューラルネットワークの一回の学習を一つの訓練入力で行います(ちょうど人間がそうするように)。オンライン学習の長所と短所を一つずつ、確率的勾配降下法のミニバッチの大きさが $20$ の場合と比較して挙げてください。
本節の結びに勾配降下法に慣れていない人をしばしば悩ませる点を議論させてください。ニューラルネットワークにおけるコスト $C$ は、当然ながら、複数の変数の関数であり - 全ての重みとバイアス - それゆえに非常に高次元な空間上の曲面であるともいえます。一部の人はこのとき、"私はこれらの超次元の可視化ができるようになる必要がある"と考え、困ってしまいます。そして彼らは心配しはじめます:"私は四次元で考えることができないし、五次元(あるいは五百万次元)なんてもっと無理だ"。彼らには"真の"数学者が持っている何か特別な能力が欠けているのでしょうか?勿論、答えはノーです。本職の数学者でも四次元の可視化はできませんし、それ以上についてはなおさらです。彼らは別の表現方法を開発するというトリックを使っているのです。それはちょうどこれまで私たちがやってきた: $C$ を減少させる方法を明らかにする $\Delta C$ の代数表現です(視覚化ではなく)。高次元について考えるのが得意な人は頭の中にこの種の多種多様なテクニックをライブラリとして持っています;私たちの代数的トリックもその一つです。これらのテクニックには私たちの慣れている三次元を視覚化する時の簡素性は持ってませんが、ひとたびそういったテクニックのライブラリを確立すれば、あなたは高次元について考えることがとても得意になるでしょう。私はこれ以上この詳細に入っていきませんが、もしあなたに興味があるなら、本職の数学者が高次元の思考に用いるテクニックのこの議論 を読んで楽しめるでしょう。いくつかのテクニックに関する議論は非常に難解ですが、たくさんの素晴らしいコンテンツが直観的でとっつきやすく、そして、全ての人が習得できるものです。
数字を分類するニューラルネットワークの実装
それでは、手書き数字を認識する方法を学ぶプログラムを作成していきましょう。その際、確率的勾配降下法とMNISTの訓練データを使用します。 最初に私たちはMNISTデータを手に入れる必要があります。もしあなたがgitのユーザーならば、下記のリポジトリからクローンすることでデータを取得できます。
git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git
もしgit のユーザーではない場合は、あなたはここからデータとコードをダウンロードすることができます。
そういえば、以前MNISTデータを説明したとき、MNISTデータは60,000枚の訓練用画像と 10,000枚の試験用画像に分かれているって言いましたよね。じつは、データの分け方を少々変えようと思います。 試験用画像はそのままにして、60,000枚の訓練用画像のうち、50,000枚を訓練のために使い、10,000枚は 検証データセットとしてとっておきます。検証データはこの章では使いませんが、本書の後の方で ハイパーパラメータを設定するのに重宝します。ハイパーパラメータとは、学習率など、 学習アルゴリズムで直接選択できないもののことです。検証データセットは元々のMNIST仕様には含まれていませんが、 多くの人はMNISTをこのやり方で使っていますし、検証データはニューラルネットワークではよく使われます。 今後、「MNIST訓練データ」と言った場合は、 オリジナルの60,000枚の画像セットではなく、今作った 50,000枚の画像からなるデータセットのことを指すこととします。 * *前述したように、MNISTデータセットは、アメリカ国立標準技術研究所(NIST)によって定義されているものです。 MNISTを構築するために、NISTデータはYann LeCun, Corinna Cortes, Christopher J. C. Burgesによって整理・より便利なフォーマットを追加されました。 詳しいことには、こちらのリンクを見てください。私のレポジトリの中のこのデータセットは、Pythonによって読み込みしやすく、操作しやすいフォーマットになっています。 このデータのフォーマットは、モントリオール大学のLISA machine learning laboratory (link)から取得しました。
MNISTデータとは別に、高速に線形代数を解くことができるNumpyと呼ばれるPythonライブラリーが必要です。 もしあなたがNumpyをインストールしていないならば、ここから手に入れてください。
それでは、完全なプログラムリストを示す前に、ニューラルネットワークのコードのコア機能の説明を以下でしましょう。 コードの中心部はNetworkクラスであり、ニューラルネットワークを表現するために使います。以下が、Networkを初期化するためのコードです。
class Network():
def __init__(self, sizes):
self.num_layers = len(sizes)
self.sizes = sizes
self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
self.weights = [np.random.randn(y, x)
for x, y in zip(sizes[:-1], sizes[1:])]
sizesは、それぞれの層におけるニューロンの数を表しています。 もし1層目に2つのニューロン、2層目に3つのニューロン、最終層に1つのニューロンを持つNetworkを作りたいならば、以下のようにコードを定義します。
net = Network([2, 3, 1])
Numpy内の行列のリストとしてバイアスと重みは保存されることについても注意してください。 なので、net.weights[1]は、2層目と3層目をつなぐ重みを保存するNumpyの行列です。(Pythonのインデックスは 0から開始されるので、1層目と2層目を繋ぐ重みではありません。) net.weights[1]という記述は冗長なので、ここでは$w$という行列として示しましょう。 それは、$w_{jk}$という行列で表現されていて、 2層目の$k$番目のニューロンと3層目の$j$番目のニューロンを繋ぐ重みです。この$j$と$k$の順序は奇妙に見えるかもしれません。 確かに$j$と$k$を交換するほうが理に適っていそうです。この順序の大きな利点は、ニューロン3層目の活性化のベクトルは以下を意味することです。 \begin{eqnarray} a' = \sigma(w a + b). \tag{22}\end{eqnarray} この式では、かなり多くの振る舞いがあるので一つ一つ紐解いてみましょう。$a$は2層目の活性化のベクトルです。$a'$を得るために、私たちは$a$と重み行列$w$を掛け算し、バイアスのベクトル$b$を足し算します。 私たちは、ベクトル$w a +b$に関数$\sigma$を作用させます。(これは関数$\sigma$のvectorizingと呼ばれます。) 等式 (22) が、シグモイドニューロンの出力を計算するための 等式 (4) と同じ結果になることを確認するのは簡単です。
Exercise
- Equation (22) をベクトルの要素を記述し、そしてシグモイドニューロンの出力を計算するための Equation (4) と同じ結果を与えることを確認しましょう。
こうした流れで、Network から出力を計算するコードを記述するのは簡単なことがわかります。 シグモイド関数を定義することからはじめます。このとき、シグモイド関数はベクトル形式でNumpyを使って定義します。
def sigmoid(z):
return 1.0/(1.0+np.exp(-z))
sigmoid_vec = np.vectorize(sigmoid)
def feedforward(self, a):
"""Return the output of the network if "a" is input."""
for b, w in zip(self.biases, self.weights):
a = sigmoid_vec(np.dot(w, a)+b)
return a
もちろん、Networkにしてほしいことは学習することです。 そのために確率的勾配降下法(SGD)を使用します。 コードはここに記します。少しばかり不可解な場所がありますが、それについては下記で解説していきます。
def SGD(self, training_data, epochs, mini_batch_size, eta,
test_data=None):
"""Train the neural network using mini-batch stochastic
gradient descent. The "training_data" is a list of tuples
"(x, y)" representing the training inputs and the desired
outputs. The other non-optional parameters are
self-explanatory. If "test_data" is provided then the
network will be evaluated against the test data after each
epoch, and partial progress printed out. This is useful for
tracking progress, but slows things down substantially."""
if test_data: n_test = len(test_data)
n = len(training_data)
for j in xrange(epochs):
random.shuffle(training_data)
mini_batches = [
training_data[k:k+mini_batch_size]
for k in xrange(0, n, mini_batch_size)]
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch, eta)
if test_data:
print "Epoch {0}: {1} / {2}".format(
j, self.evaluate(test_data), n_test)
else:
print "Epoch {0} complete".format(j)
training_dataは、訓練入力と対応した目的出力の組(x, y)のリストです。 変数epochsとmini_batch_sizeは訓練のための世代数と、サンプリングするときに使用するミニバッチの大きさです。 変数etaは学習率$\eta$です。 もしオプションの引数test_dataがある場合、プログラムは各訓練のエポックのあとにネットワークを評価して、現在の進行状況を出力します。 この機能は性能改善の進行状況を確認するときに役に立ちますが、計算に少し時間がかかるようになります。
コードは以下のように機能します。各エポックでは、訓練データをランダムにシャッフルすることによって開始し、適切なサイズのミニバッチに分割します。 このコードは、訓練データからランダムにサンプルする簡単な方法になります。 各ミニバッチに、勾配降下法を1ステップ実行します。これは、コードself.update_mini_batch(mini_batch, eta)によって行われ、 ミニバッチの訓練データだけを使用して勾配降下法を実行し、ネットワークの重みとバイアスを更新します。ここに、update_mini_batchのコードを示します。
def update_mini_batch(self, mini_batch, eta):
"""Update the network's weights and biases by applying
gradient descent using backpropagation to a single mini batch.
The "mini_batch" is a list of tuples "(x, y)", and "eta"
is the learning rate."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
self.backpropのコードは今すぐには説明しません。次の章で誤差逆伝播法について勉強し、その際にself.backpropのコードを紹介します。 なので今は、訓練データのxに関連するコストに対して適切な勾配を返す働きをするということを前提にします。
それでは、下記の完全なプログラムを見てください。この際、説明を省略した部分や説明文を含んでいます。 self.backpropを除いて、プログラムは明快であり、すでにお話しした通り、全ての処理の重い部分はself.SGDとself.update_mini_batchで行われています。 self.backpropは勾配を計算することを手助けするためのいくつかの追加機能を使用しており、詳細はここでは説明しませんが、 $\sigma$関数の導関数を計算するsigmoid_prime、ベクトル形式のsigmoid_prime_vecとself.cost_derivativeです。 次の章で詳細を確認しますが、コードと説明を見る事によって要点を理解する事ができます。 プログラムが長いように見えますが、多くはプログラム内の理解を促すための解説文であり、コード自体は理解が簡単に書いているつもりです。 実際、プログラムはたった空行と解説を除いて74行です。 コードのすべてはGitHubで見つけることができます。
"""
network.py
~~~~~~~~~~
A module to implement the stochastic gradient descent learning
algorithm for a feedforward neural network. Gradients are calculated
using backpropagation. Note that I have focused on making the code
simple, easily readable, and easily modifiable. It is not optimized,
and omits many desirable features.
"""
#### Libraries
# Standard library
import random
# Third-party libraries
import numpy as np
class Network():
def __init__(self, sizes):
"""The list ``sizes`` contains the number of neurons in the
respective layers of the network. For example, if the list
was [2, 3, 1] then it would be a three-layer network, with the
first layer containing 2 neurons, the second layer 3 neurons,
and the third layer 1 neuron. The biases and weights for the
network are initialized randomly, using a Gaussian
distribution with mean 0, and variance 1. Note that the first
layer is assumed to be an input layer, and by convention we
won't set any biases for those neurons, since biases are only
ever used in computing the outputs from later layers."""
self.num_layers = len(sizes)
self.sizes = sizes
self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
self.weights = [np.random.randn(y, x)
for x, y in zip(sizes[:-1], sizes[1:])]
def feedforward(self, a):
"""Return the output of the network if ``a`` is input."""
for b, w in zip(self.biases, self.weights):
a = sigmoid_vec(np.dot(w, a)+b)
return a
def SGD(self, training_data, epochs, mini_batch_size, eta,
test_data=None):
"""Train the neural network using mini-batch stochastic
gradient descent. The ``training_data`` is a list of tuples
``(x, y)`` representing the training inputs and the desired
outputs. The other non-optional parameters are
self-explanatory. If ``test_data`` is provided then the
network will be evaluated against the test data after each
epoch, and partial progress printed out. This is useful for
tracking progress, but slows things down substantially."""
if test_data: n_test = len(test_data)
n = len(training_data)
for j in xrange(epochs):
random.shuffle(training_data)
mini_batches = [
training_data[k:k+mini_batch_size]
for k in xrange(0, n, mini_batch_size)]
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch, eta)
if test_data:
print "Epoch {0}: {1} / {2}".format(
j, self.evaluate(test_data), n_test)
else:
print "Epoch {0} complete".format(j)
def update_mini_batch(self, mini_batch, eta):
"""Update the network's weights and biases by applying
gradient descent using backpropagation to a single mini batch.
The ``mini_batch`` is a list of tuples ``(x, y)``, and ``eta``
is the learning rate."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]
def backprop(self, x, y):
"""Return a tuple ``(nabla_b, nabla_w)`` representing the
gradient for the cost function C_x. ``nabla_b`` and
``nabla_w`` are layer-by-layer lists of numpy arrays, similar
to ``self.biases`` and ``self.weights``."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
# feedforward
activation = x
activations = [x] # list to store all the activations, layer by layer
zs = [] # list to store all the z vectors, layer by layer
for b, w in zip(self.biases, self.weights):
z = np.dot(w, activation)+b
zs.append(z)
activation = sigmoid_vec(z)
activations.append(activation)
# backward pass
delta = self.cost_derivative(activations[-1], y) * \
sigmoid_prime_vec(zs[-1])
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
# Note that the variable l in the loop below is used a little
# differently to the notation in Chapter 2 of the book. Here,
# l = 1 means the last layer of neurons, l = 2 is the
# second-last layer, and so on. It's a renumbering of the
# scheme in the book, used here to take advantage of the fact
# that Python can use negative indices in lists.
for l in xrange(2, self.num_layers):
z = zs[-l]
spv = sigmoid_prime_vec(z)
delta = np.dot(self.weights[-l+1].transpose(), delta) * spv
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
return (nabla_b, nabla_w)
def evaluate(self, test_data):
"""Return the number of test inputs for which the neural
network outputs the correct result. Note that the neural
network's output is assumed to be the index of whichever
neuron in the final layer has the highest activation."""
test_results = [(np.argmax(self.feedforward(x)), y)
for (x, y) in test_data]
return sum(int(x == y) for (x, y) in test_results)
def cost_derivative(self, output_activations, y):
"""Return the vector of partial derivatives \partial C_x /
\partial a for the output activations."""
return (output_activations-y)
#### Miscellaneous functions
def sigmoid(z):
"""The sigmoid function."""
return 1.0/(1.0+np.exp(-z))
sigmoid_vec = np.vectorize(sigmoid)
def sigmoid_prime(z):
"""Derivative of the sigmoid function."""
return sigmoid(z)*(1-sigmoid(z))
sigmoid_prime_vec = np.vectorize(sigmoid_prime)
それでは、このコードがどれだけ良く手書き数字を認識できるかを確認していきましょう。 まずはMNISTデータをダウンロードするところからはじめてみよう。 ここではmnist_loader.pyを使用します。以下のコマンドをpythonシェルで実行してください。
>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
もちろん、これは独立したpythonプログラムとして実行できますが、 ここまで従ってきたならば、pythonシェルで簡単に処理できるでしょう。
MNISTデータをダウンロードした後、私たちは$30$個の隠れニューロンをもつNetworkを設定します。 私たちはnetworkと名前を付けた上記のpythonプログラムをインポートした後に、この処理を行います。
>>> import network
>>> net = network.Network([784, 30, 10])
最後に、30世代・ミニバッチサイズ10・訓練率$\eta = 3.0$の条件で、MNISTのtraining_dataから確率的勾配降下法を使用して学習します。
>>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
もしこの文章を読みながらコードを実行しているならば、この計算は少々時間がかかるので注意してください。 2014年における一般的なスペックのパソコンならば、訓練の1世代ごとに数分程度かかります。 計算を実行しつつ、読み続けて、たまに計算結果を確認することをおすすめします。 もしあなたが急いでいる場合は、あなたは世代数を減らすか、隠れニューロンの数を減らすか、訓練データの一部のみ使用することによって計算を速くすることができます。 実際の商用コードはより速く計算が可能ですが、 このpythonコードはニューラルネットワークを理解することを助けることが目的であるため、計算が早いわけではありません。 もちろん、一度ニューラルネットワークを訓練すれば、私たちは多くのコンピュータープラットホーム上で非常に高速に実行することができます。 例えば、ニューラルネットワークの重みとバイアスの良いセットがあれば、webブラウザのJavascriptや、携帯デバイスのアプリに移植し、実行するのは簡単です。 それでは以下に、ニューラルネットワークのある訓練プロセスの一部の結果を示しましょう。 この出力は訓練のエポックごとにニューラルネットワークを使用して適切に訓練データを認識できた数を表しています。 最初の世代が終わったあとに10000個中の9129個が正しく認識できており、その後は増加し続けていることがわかります。
Epoch 0: 9129 / 10000
Epoch 1: 9295 / 10000
Epoch 2: 9348 / 10000
...
Epoch 27: 9528 / 10000
Epoch 28: 9542 / 10000
Epoch 29: 9534 / 10000
訓練されたネットワークは95%の分類率を有しており、ピーク性能は28世代での95.42%でした。 この結果は、最初の試みとしては大変有望です。 ネットワークをランダムな重みとバイアスによって初期化しているので、 このコードを実行したとしても、上記で示した値と全く一緒になるとは限らないことに注意してください。 この章では、3回の計算のうちのベストの解を示しています。
それでは、隠れニューロンの数を100個にして上記の実験を再計算してみましょう。 この計算も同様に時間がかかりますので、計算を実行しつつ読み進めることが賢明です。(今回の場合、隠れニューロンの数が多いので各世代での計算時間がよりかかるので。)
>>> net = network.Network([784, 100, 10])
>>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
予想通り、この計算では性能が96.59%に向上しました。 少なくともこのケースでは、より多くの隠れ層を使用することでより良い結果を得ることが出来ます。* *読者のフィードバックによると、この実験では性能の違いが報告されており、いくつかの計算結果ではかなり性能が悪くなるようです。 3章で紹介するテクニックを使用することで、計算ごとの予測性能の違いを劇的に減らすことができます。
もちろん、これらの精度を獲得するために、訓練のエポック数、ミニバッチのサイズ、学習率$\eta$を具体的に選択しなくてはなりませんでした。 上記のように、学習アルゴリズムによって学習するパラメータ(重みとバイアス)と区別するために、これらはニューラルネットワークのハイパーパラメータとして呼ばれています。 もしハイパーパラメータを不適切に選択したならば、悪い結果を得ることになります。例えば、学習率$\eta = 0.001$を選んだとすると、
>>> net = network.Network([784, 100, 10])
>>> net.SGD(training_data, 30, 10, 0.001, test_data=test_data)
結果の改善の進捗は遅くなってしまいます。
Epoch 0: 1139 / 10000
Epoch 1: 1136 / 10000
Epoch 2: 1135 / 10000
...
Epoch 27: 2101 / 10000
Epoch 28: 2123 / 10000
Epoch 29: 2142 / 10000
たいていの場合、ニューラルネットワークをデバッグすることは困難なことであると言えます。 ハイパーパラメータの初期の選択が悪く、ランダムノイズとほぼ同然の結果しか得られないときは、特に困難です。 私たちは前に使用した隠れニューロンが30個のネットワークにおいて、学習率を$\eta = 100.0$に変更した場合を仮定してみましょう。
>>> net = network.Network([784, 30, 10])
>>> net.SGD(training_data, 30, 10, 100.0, test_data=test_data)
Epoch 0: 1009 / 10000
Epoch 1: 1009 / 10000
Epoch 2: 1009 / 10000
Epoch 3: 1009 / 10000
...
Epoch 27: 982 / 10000
Epoch 28: 982 / 10000
Epoch 29: 982 / 10000
これらの疑問を取り除くためのニューラルネットワークのデバッグとしてのレッスンは些細な問題ではありません、そして通常のプログラミングに関して言えば、関係した技術があります。 ニューラルネットワークから良い結果を得るためのデバッグ技術を学ぶ必要があります。 より一般的に言えば、私たちは良いハイパーパラメータと良いアーキテクチャを選択するためのヒューリスティック技術を開発する必要があります。 この本を通して、上記のハイパーパラメータの設定方法を含むこれらの技術について解説します。
Exercise
- 隠れ層がない入力層と出力層のみの2層のネットワークを作ってみてください。それぞれニューロンは、784個と10個です。そして、確率的勾配法で学習させてみてください。どんな分類精度を達成できるでしょうか。
以前、MNISTデータのロード方法の詳細について説明を省略していました。かなり簡単ではありますが、念のためにコードを以下に載せました。 MNISTデータを格納するために使われるデータ構造は、資料内の解説にある通りで、Numpyのndarrayオブジェクトです。(もしndarrayに馴染みがない方は、ベクトルとして考えてください。)
"""
mnist_loader
~~~~~~~~~~~~
A library to load the MNIST image data. For details of the data
structures that are returned, see the doc strings for ``load_data``
and ``load_data_wrapper``. In practice, ``load_data_wrapper`` is the
function usually called by our neural network code.
"""
#### Libraries
# Standard library
import cPickle
import gzip
# Third-party libraries
import numpy as np
def load_data():
"""Return the MNIST data as a tuple containing the training data,
the validation data, and the test data.
The ``training_data`` is returned as a tuple with two entries.
The first entry contains the actual training images. This is a
numpy ndarray with 50,000 entries. Each entry is, in turn, a
numpy ndarray with 784 values, representing the 28 * 28 = 784
pixels in a single MNIST image.
The second entry in the ``training_data`` tuple is a numpy ndarray
containing 50,000 entries. Those entries are just the digit
values (0...9) for the corresponding images contained in the first
entry of the tuple.
The ``validation_data`` and ``test_data`` are similar, except
each contains only 10,000 images.
This is a nice data format, but for use in neural networks it's
helpful to modify the format of the ``training_data`` a little.
That's done in the wrapper function ``load_data_wrapper()``, see
below.
"""
f = gzip.open('../data/mnist.pkl.gz', 'rb')
training_data, validation_data, test_data = cPickle.load(f)
f.close()
return (training_data, validation_data, test_data)
def load_data_wrapper():
"""Return a tuple containing ``(training_data, validation_data,
test_data)``. Based on ``load_data``, but the format is more
convenient for use in our implementation of neural networks.
In particular, ``training_data`` is a list containing 50,000
2-tuples ``(x, y)``. ``x`` is a 784-dimensional numpy.ndarray
containing the input image. ``y`` is a 10-dimensional
numpy.ndarray representing the unit vector corresponding to the
correct digit for ``x``.
``validation_data`` and ``test_data`` are lists containing 10,000
2-tuples ``(x, y)``. In each case, ``x`` is a 784-dimensional
numpy.ndarry containing the input image, and ``y`` is the
corresponding classification, i.e., the digit values (integers)
corresponding to ``x``.
Obviously, this means we're using slightly different formats for
the training data and the validation / test data. These formats
turn out to be the most convenient for use in our neural network
code."""
tr_d, va_d, te_d = load_data()
training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]
training_results = [vectorized_result(y) for y in tr_d[1]]
training_data = zip(training_inputs, training_results)
validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
validation_data = zip(validation_inputs, va_d[1])
test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
test_data = zip(test_inputs, te_d[1])
return (training_data, validation_data, test_data)
def vectorized_result(j):
"""Return a 10-dimensional unit vector with a 1.0 in the jth
position and zeroes elsewhere. This is used to convert a digit
(0...9) into a corresponding desired output from the neural
network."""
e = np.zeros((10, 1))
e[j] = 1.0
return e
このプログラムはかなり良い結果を得られたと言いました。これはどういう意味でしょうか。 何と比較して良いと言っているのでしょうか。お互いに比較したり、何がよい実行結果なのかを理解したりするために、いくつかのニューラルネットワークではない単純な性能基準を持つことは有益です。 もちろん、全ての中で最もシンプルな基準は数字をランダムに推測するものです。それは、性能は10%程度になるでしょう。私たちは、それよりも遥かに良い性能を持っています。
取るに足らなくない基準とはなんでしょうか。それでは、とてもシンプルなアイデアに挑戦してみましょう。 画像がどれくらいか暗いかについて見ています。例えば、「2」の画像は「1」の画像に比べて、より暗い画像となります。 なぜならば、下記の例を見ればわかる通り、多くのピクセルが黒く塗りつぶされているからです。

これは、各数字($0, 1, 2,\ldots, 9$)の黒色を持つピクセルの平均を計算するために訓練データを使用することを提案しています。 新しい画像が示されたとき、画像がどれだけ黒いかを計算し、最も近い黒色を持つピクセルの平均の数字として区別します。 これは簡単な手順であり、コーディングも簡単です。私は明示的にコードを書きませんが、GitHubのGitHub repositoryに公開しておきます。しかし、この方法では、10000枚の訓練データのうち2225枚を適切に区別することができ、つまり22.25%の精度、ランダム推測に比べて大きな改善をもたらします。
予測精度20から50%程度の他のアイデアを見つけることは難しくありません。 もしあなたが少し頑張れば、予測精度50%に到達できるでしょう。 しかしさらに高精度を取得するためには、機械学習アルゴリズムを使用することが手助けになるでしょう。 良く知られている手法の一つであるサポートベクターマシン(SVM)について挑戦してみましょう。 もしSVMに馴染みがなかったとしても、心配しないでください。SVMの働きについて詳細に理解する必要はありません。 代わりに、私たちはLIBSVMとして知られているSVMの高速なCベースのライブラリのpythonインターフェースであるscikit-learnというライブラリを使用します。
もしscikit-learnのSVM分類器のデフォルト設定で計算したとすれば、10000個の画像中の9435個を適切に分類できます。(コードはここにあります。) 黒色の平均値に基づく分類から考えると、とても大きな改善です。 確かに、SVMはだいたいニューラルネットワークと同じくらいか、ちょっと悪いくらいの性能を持っています。 後の章では、私たちはSVMをはるかに超える良い性能を得るために、ニューラルネットワークを改良する新技術を紹介します。
話はこれで終わりではありません。 10000個中の9435個の適切な分類は、scikit-learnのデフォルト設定のSVMによるものでした。 SVMは調整可能なパラメータをいくつか持っていて、さらに性能の良い判別が行うことができるパラメータを探すことができる可能性があります。 この探索を明示的には行いませんが、代わりにもし詳細を知りたいならばAndreas Muellerのブログを確認してください。 Muellerは、SVMのパラメータを最適化することで、98.5%の予測性能に到達していることを示しています。 言い換えれば、適切にチューニングされたSVMでは間違いを70個しかしないことになります。これは、かなり良い性能です。ニューラルネットワークはこれより良い推定ができるでしょうか。
実際には可能です。現在、よく設計されたニューラルネットワークは、SVMを含めて他のMNISTの識字アルゴリズムの中で最も優れています。 2014年現在の記録では、10000個中9979個の画像を適切に分類することが出来ています。 これは、Li Wan、 Matthew Zeiler,、Sixin Zhang、Yann LeCun、 Rob Fergusによって行われたものです。 この本の中の後半で、彼らが使用した技術の多くを見ることができます。その性能のレベルは人間とほぼ同等であり、おそらくより良いものです。 なぜならば、人間が自信を持って認識することさえ難しいMNIST画像がいくつかあるからです。例えば以下のようなものです。
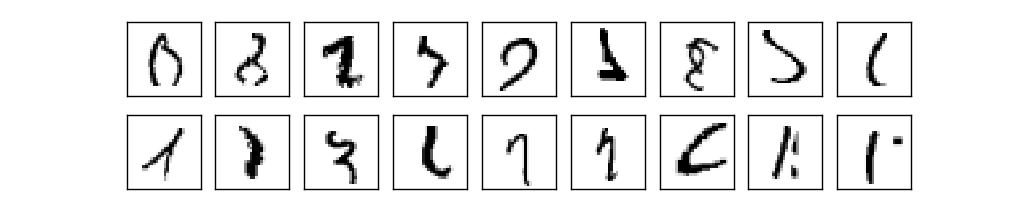
これらを分類するのは難しいと認めることを確信しています。MNISTデータセットの中でこのような画像があるのにもかかわらず、ニューラルネットワークは10000個の画像の中の21個以外は適切に分類できることは驚くべきことです。 プログラミングをするとき、たいていはMNISTの識字を理解するような複雑な問題を解くことは、高度なアルゴリズムが必要だと考えています。 しかし、Wanらのペーパーの中で言及したニューラルネットワークはかなりシンプルなアルゴリズムを意味しています。私たちがこの章で見てきたアルゴリズムのバリエーションも含んでいます。
Deep Learningに向けて
ニューラルネットワークは印象的な性能を提供していますが、その性能はやや神秘的です。 ネットワークの重みとバイアスが自動的に発見されました。 これはつまり、ネットワークがどのように機能しているかについて説明できないことを意味します。 ネットワークが手書き数字を分類する原理を理解する方法を見つけることができるでしょうか? そして、そのような原理を考え、さらによりよく出来るでしょうか?
この質問により厳密に答えるために、向こう20~30年でニューラルネットワークは人工知能(AI)になるだろうと考えてください。 私たちは、そんな賢いネットワークがどのように働くかを理解できるでしょうか。 もしかしたら、私たちが把握していない重みとバイアスを使ったネットワークは、不透明なものになるかもしれない。 というのも、ネットワークは自動的に学習してきたからです。 初期のAI研究者は、AIを構築するための努力によって知能の原理(人間の脳機能のような)を理解できるようになる、そんなことを望んでいました。 しかし、私たちは脳だけでなく、人工知能の働きさえ理解せずに終わってしまうことになるかもしれません!
これらの問題に答えるために、この章の最初に説明した人工ニューロンのパーセプトロンについて振り返ってみましょう。画像が人の顔を示しているか否かを判断したいとします。
Credits: 1. Ester Inbar. 2. Unknown. 3. NASA, ESA, G. Illingworth, D. Magee, and P. Oesch (University of California, Santa Cruz), R. Bouwens (Leiden University), and the HUDF09 Team. Click on the images for more details.
この問題に対しても、手書き文字認識と同じ方法で取り組むことができます。つまり、ニューラルネットワークの入力として画像のピクセルを使い、1つの出力ニューロンによって「顔である」か「顔でない」かを判定させるのです。
では考えてみましょう。ただし、学習アルゴリズムは使いません。 その代わりに、ネットワークを手動で設計し、適切な重みとバイアスを設定していきます。 どのように取り組めばよいでしょうか?ニューラルネットワークを一瞬全て忘れるとして、私たちが使うことのできるヒューリスティクスによって問題を小さな問題に分割します。 「画像の左上に目はあるか」「画像の右上に目はあるか」「画像の中心に鼻はあるか」「画像の中央下に口はあるか」「髪の毛は上のほうにあるか」などなど。
これらの質問の答えのいくつかが「YES」や「おそらくYES」だとすれば、その画像は顔であると言えるでしょう。逆に、質問の答えがほとんど「NO」だとすれば、それはおそらく顔ではないでしょう。
もちろん、これはかなり荒いヒューリスティクスであり、多くの欠点を持ちます。 例えば、禿げた人を考えた場合は、彼らには髪の毛がありません。 私たちは、顔の一部のみだったり、顔に角度がついていたり、顔の一部が隠されていたりしても、顔だと判断できます。 それでも、このヒューリスティクスによって次のような示唆を得ることができます。 つまり、小さい問題をニューラルネットワークを使って解くことができるなら、それらネットワークを組み合わせることで、顔判定のためのネットワークを構築することができる、ということです。 以下に、ありうりそうなアーキテクチャを示しましょう。これは、サブネットワークを長方形で表しています。 ただし、ここでは顔認識問題を解くための現実的なアプローチは意図していないことに注意してください。 むしろこれは、どのようにネットワークが機能するかについて直感的な理解を促してくれます。
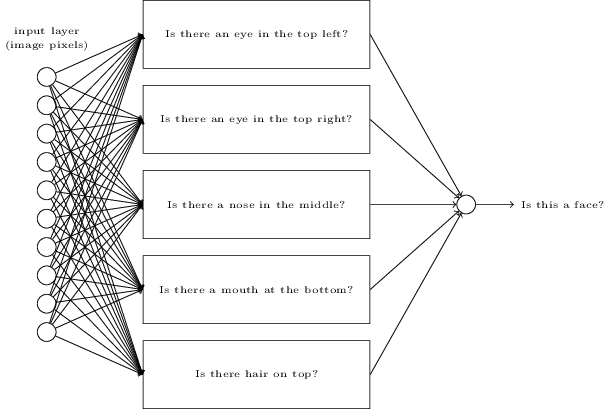
サブネットワーク自体も小さく分解できる、というのはいかにもありそうなことです。 それでは次のような質問について検討してみましょう。 「画像の左上に目があるか?」これは次のような質問にさらに分けることができます。 「眉毛はあるか?」「まつ毛はあるか?」「眼球の光彩はあるか?」などです。 もちろんこれらの質問は、実際は位置の情報を含んでいるべきです。 「画像の右上に眉毛はあるか?それは光彩の上にあるか?」というように。 このような感じですが、シンプルにはしておきましょう。このようにして、「左上に目はあるか?」は次のように分解できます。
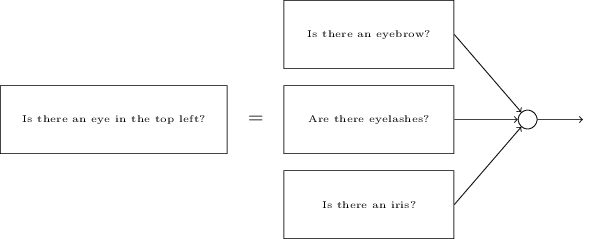
こういった質問は、複数の層を介して、さらにさらに分解して行くことが可能です。 究極的には、単一のピクセルレベルで簡単に答えられるようなシンプルな質問に答えるサブネットワークで作業することになります。 例えばその質問は、画像内のある特定の点での、シンプルな形状の有り・無しかもしれません。 その手の質問は、画像のピクセルにそのまま直接接続された、単一のニューロンによって答えることができます。
最終的な結果は、非常に込み入った問題(「画像は顔を表しているか否か」のような)を、単一のピクセルレベルで答えられる問題に分解したネットワークになります。 以上の結果を得るためには、入力画像についてとても簡単で特定の質問に答える初期の層と、より複雑で抽象的な概念の階層を構築している後半の層を含む多くの層を通ることが必要です。 多くの隠れ層(2つかそれ以上)を含む多層構造のネットワークは、ディープニューラルネットワークと呼ばれています。
もちろん、どのように再帰的にサブネットワークに分けていくのかについては、述べていません。 ネットワーク内の重みとバイアスを手動で設計するのは、実用的ではありません。 代わりに訓練データから、自動的に重みとバイアス(さらに言えば、概念の階層構造まで)を習得できるような学習アルゴリズムを使います。 1980年代と1990年代の研究者は、確率的勾配降下法と誤差逆伝播法をディープネットワークの訓練に使用してみようとしました。 残念ながら、いくつかの特別なアーキテクチャを除いて、彼らは良い結果を得られませんでした。 学習はするのですが、とても遅く、現実的に使用できませんでした。
2006年になってようやく、ディープニューラルネットを学習可能にする一連の技術が開発されました これらの学習技術は確率的勾配降下法と誤差逆伝播法に基づいてはいますが、新しいアイデアが追加されています。 これらの技術は、より深く(そしてより大きな)ネットワークを訓練可能にし、現在では5~10層のネットワークが当然のように訓練されています。 そして、浅いニューラルネットワーク(特に隠れ層が1層のみの場合)よりも、多くの問題解決において非常に良くなっていることがわかりました。 もちろんこれは、ディープネットワークが、概念の複雑な階層構造を構築できるからです。 従来のプログラム言語で複雑なプログラムを作るときによく使う、モジュール方式のデザインと考え方に少し似ています。 ディープネットワークと浅いネットワークの関係は、関数作成と呼び出しが可能なプログラム言語と、そのような能力を持たない言語の関係に少し似ています。 抽象化は、従来のプログラミングにおけるものとは異なる形式を取りますが、それは極めて重要なことなのです。