自身が、コンピュータを一から設計するよう求められているエンジニアであると想像してみてください。
あなたはある日、オフィスの外にいます。
論理回路を設計するため、ANDゲートやORゲートから手を付け始めています。そこへ、あなたの上司が悪い知らせを持ってきました。
顧客が驚くべき設計要件を追加したのです。それは、コンピュータ全体をたった2層の深さの回路で作れという要件でした。
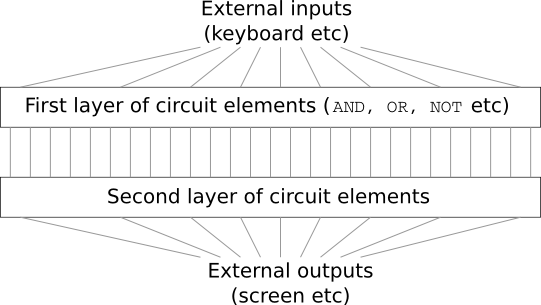
あなたは慌てて、上司に言いました。 「この顧客は狂っています!」
「彼らは狂ってると私も思う。でも、顧客が望むものは提供するしかないんだ」と上司は答えます。
実際には、顧客が狂ってるわけではありません。
どんなに入力が多くてもANDを取得できる、特別な論理ゲートを使えると想定してみてください。
加えて、多入力のNANDを取得できる論理ゲートも使えるとします。
このNANDゲートは、複数入力のANDを取得し、その結果を反転させて出力するゲートです。
これらの特別な論理ゲートを使えば、ちょうど2層の回路で、どんな関数でも計算できます。
でも、実現可能だからと言って、良いアイデアとは限りません。 実際、回路設計問題(もしくはアルゴリズムのあらゆる問題)を解くときには、私たちはまず、部分問題から解き始めます。 そして、徐々に部分問題の解を組み合わせていくのです。 すなわち、多数の層の解を抽象化させて、全体の解を作り上げていきます。
たとえば、2つの数の掛け算を行う論理回路を設計するとしましょう。 きっとあなたは、2つの数の足し算を行う部分回路を組み合わせたいと思います。 そして2つの数の足し算を行う部分回路を作るときには、今度は、2つのビットの足し算を行う、部分-部分回路を組み合わせるでしょう。 大ざっぱに言うと、設計した論理回路はこんな形をしています。
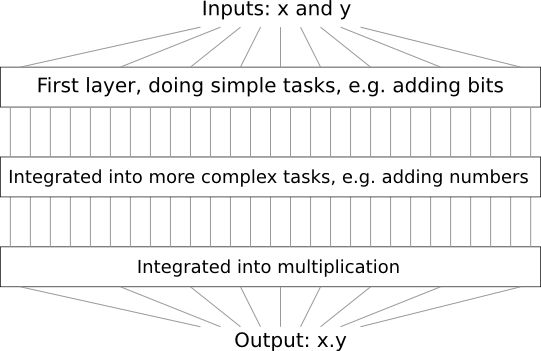
最終的な論理回路は、少なくとも3層の回路要素から構成されます。 私が述べたものよりも、さらに部分問題にブレークダウンしていけば、3層以上含むことになるでしょう。 ただ、これまでの話の中で、あなたは汎用的に使えるアイデアを得たはずです。
このように、回路を深くすれば、設計は簡単になっていきます。 でも設計が楽になるだけではありません。 実際、同じ計算を行う際、深い回路に比べると、浅い回路を使う場合には指数関数的に多くの回路要素が必要となることが、数学的に証明されています。 たとえば、1984年のFurst、Saxe、そしてSipserの有名な論文* * Parity, Circuits, and the Polynomial-Time Hierarchy, by Merrick Furst, James B. Saxe, and Michael Sipser (1984) を確認してください。 では、ビットのパリティを計算する際に、浅い回路を用いると、指数関数的に多くのゲートが必要となることが示されています。 一方で、深い回路を使うとなれば、小さな回路要素でパリティ計算できます。 そのときには、まずビットの組のパリティを計算します。 その結果を使って、ビットの組の組のパリティを計算します。 それを繰り返して、全体のパリティを素早く計算できます。 深い回路は浅い回路よりも、本質的に遥かに強力なのです。
これまで、この本はニューラルネットワークに対して、先ほど述べた狂った顧客のような取り組み方をしてきました。 すなわち、これまで扱ってきたほぼ全てのネットワークは、たった一つの隠れ層(に加えて入力層と出力層)しか持っていませんでした。
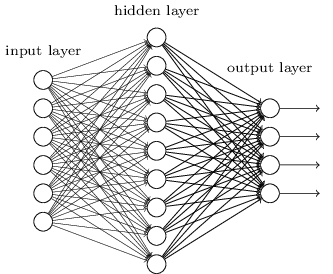
これらのシンプルなネットワークは、驚くほど有用です。 前章までに、このネットワークを使った手書き数字の分類で、98%以上の精度を出しました! それにも関わらず、多くの隠れ層を備えるネットワークの方が強力なのではないか、という直感的な期待があるのです。
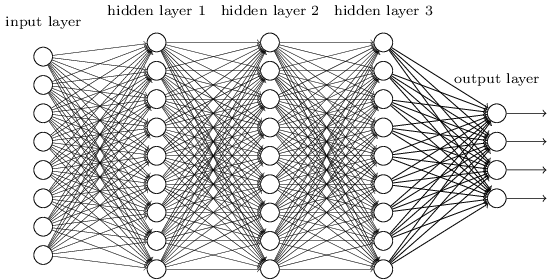
多層のネットワークは、先ほどの論理回路の例と同じように、 中間層を抽象化のために組み合わせて使います。 たとえば、私たちが視覚パターン認識をするとしましょう。 そのときには、第一層のニューロンはエッジを認識するようになります。 第二層のニューロンは、三角形や四角形などの複雑な形状を、エッジの情報から認識します。 第三層のニューロンはさらに複雑な形状を認識します。 以降はこれの繰り返しです。 どうやら、これらの抽象化層のおかげで、ニューラルネットワークは複雑なパターン認識問題を解く方法を学習できるようです。 加えて、回路の例と同じように、深いネットワークは、浅いネットワークよりも元来強力であるという理論的な結果があります* *特定の問題とネットワーク構造については、このことが以下で証明されています。 On the number of response regions of deep feed forward networks with piece-wise linear activations, by Razvan Pascanu, Guido Montúfar, and Yoshua Bengio (2014). さらなる非公式な議論については、以下のセクション2を参照してください。 Learning deep architectures for AI, by Yoshua Bengio (2009).。
このような深いネットワークを訓練するにはどうすればよいのでしょうか? この章では、働き者の学習アルゴリズムである 逆伝播による 確率的勾配降下法 を使って、深いネットワークを訓練していこうと思います。 しかしその過程で、深いネットワークを使っていても、浅いネットワークのときよりもパフォーマンスが良くならないという問題にぶつかります。
上記の議論の後では、そのような失敗が起きることが、不思議に思えるでしょう。 失敗するからと言って、深いネットワークに見切りをつけずに、深いネットワークを訓練する難しさの原因を掘り下げて、理解していきましょう。 よく観察すると、深いネットワーク中の異なる層は、まったく異なるスピードで学習していることがわかります。 特に、後ろの方の層は大きく学び、前の方の層はしばしば訓練中にもたついて、全く何も学ばなかったりします。 この前方の層のどん詰まりの状況は、単に運が悪かったというわけではありません。 むしろ、勾配を利用した学習テクニックによく見られる、学習が遅くなってしまう本質的な理由がそこにはあります。
問題を深く掘り下げていくと、対照的な現象の発生も目撃します。 前の方の層が大きく学び、後ろの方の層が学ばないという現象です。 実際、深く多層からなるニューラルネットワークの場合、勾配降下法による学習には不安定性が伴うことを学びます。 この不安定性により、前方の層か後方の層のどちらかが、訓練時に学習しなくなる傾向があります。
これは悪い知らせに聞こえます。 しかし、これらの問題を掘り下げていくと、深いネットワークを効果的に訓練するための必要事項に関して洞察を得ることができます。 そして、この調査が次の章への良い準備になるのです。 次の章では、深層学習を使って画像認識問題に取り組みます。
勾配消失問題
さて、深いネットワークを訓練しようとするときに、何が上手く行かないのでしょうか?
この問いに答えるために、隠れ層1つのみのネットワークの例を再び見てみましょう。 いつも通り、MNISTの手書き文字に対する分類問題を、学習と実験の場として使います* *MNIST の問題とデータは ここ と ここで紹介しました。
お望みなら、自身のコンピュータでネットワークを訓練して追うことができます。 もちろん、ただ読み進めるだけでも構いません。 自身で実験をしつつ内容を追いたい場合、Python 2.7、Numpy、そしてコードが必要です。 コードはコマンドラインを使ってレポジトリから複製できます。
git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git
そして、PythonのシェルからMNISTのデータをロードしてください。
>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
ネットワークをセットアップします。
>>> import network2
>>> net = network2.Network([784, 30, 10])
このネットワークは入力層に784のニューロンを持ち、これらが入力画像の $28 \times 28 = 784$ ピクセルに対応します。 30の隠れニューロンと、10の出力ニューロンを使います。この出力ニューロンがMNISTの文字の ('0', '1', '2', $\ldots$, '9') の10分類に対応します。
さあ、10個の訓練画像を含むミニバッチ、学習率は $\eta = 0.1$ 、正規化パラメータ $\lambda = 5.0$ の条件下で、ネットワークを30エポック分、訓練してみましょう。 validation data*を分類する正確さの変化を、訓練の進行にしたがい観測します* *ネットワークの訓練にはかなり時間がかかることに注意してください。 コンピュータの性能によりますが、エポックごとに最大2,3分程度かかります。 なので、コードを実行しているなら、終了を待たずにそのまま読み進めて、後で振り返るとよいでしょう。
>>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0,
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)
分類精度は96.48%(もしくは、実行するごとにちょっとだけ変化しますが大体その程度)です。 この結果は、同じ設定で実施した先の結果とほぼ同じ数値です。
さて、同じ30個のニューロンを持つ隠れ層を追加してみましょう。 このネットワークを、同じハイパーパラメータのもとで訓練します。
>>> net = network2.Network([784, 30, 30, 10])
>>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0,
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)
分類精度が向上し、96.90%となりました。 この結果は励みになります。少し深くしたことで、良い結果が得られたようです。 さあ、さらに30個のニューロンを持つ隠れ層を追加しましょう。
>>> net = network2.Network([784, 30, 30, 30, 10])
>>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0,
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)
今回は結果が良くなりませんでした。 精度が96.57%へ落ちています。 一番最初の浅いネットワークの結果に近づきました。 もう1つ隠れ層を追加しましょう。
>>> net = network2.Network([784, 30, 30, 30, 30, 10])
>>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0,
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)
分類精度は再び悪化し、96.53%となりました。 統計的に有意な悪化ではおそらくないですが、良い結果ではありません。
この振る舞いは奇妙に思えます。 直感的には、隠れ層を追加したことで、ネットワークは複雑な分類関数を学習でき、分類タスクもうまくいくはずです。 最悪の場合でも、隠れ層に単に何もさせないようにすれば、悪化しないはずなのです* *何もしない隠れ層がどう生まれるかを理解するための後に紹介する問題を確認してください。。 しかし、実際には悪化が起きています。
では一体、何が起きているのでしょう? 隠れ層を追加することで、原理的には上手くいくとすると、 問題は学習アルゴリズムが適切な重みとバイアスを探せていないことです。 学習アルゴリズムの上手くいかない点とその対処法を見つけたいです。
何が悪いのかの洞察を得るために、ネットワークの学習の様子を可視化してみましょう。 下図に、 $[784, 30, 30, 10]$ のネットワークの一部をプロットしました。 このネットワークは、2層の隠れ層を持ち、それぞれが30個のニューロンを持っています。 図の中の各ニューロンには小さなバーがあります。 このバーは、ネットワークの学習に伴ってニューロンが変化する速さを示しています。 バーが大きいと、ニューロンの重みとバイアスは急速に変化しており、 一方で、バーが小さいと、重みとバイアスの変化が遅いことを示します。 より正確に言うと、バーは各ニューロンの勾配 $\partial C / \partial b$ を示しています。 この勾配は、ニューロンのバイアスに対するコスト関数の変化率のことです。 2章で見たように、この勾配の大きさが、学習中のバイアスの変化の速さだけでなく、ニューロンに入力される重みの変化の速さも制御します。 詳細を思い出せなくても心配しないでください。 このバーは、ネットワークの学習時の、ニューロンの重みとバイアスの変化の速さだということだけ覚えておけばよいです。
図をシンプルにするために、隠れ層のうち単純に上から6個のニューロンのみ表示しました。 学習すべき重みやバイアスを持たない入力ニューロンは省略してあります。 同じ数のニューロンを持つ層ごとの比較を行いたいので、出力ニューロンも省略しました。 プロットした結果は、訓練開始時のもの、すなわちネットワークが初期化された直後のものです* *プロットしたデータは、 generate_gradient.pyを使って生成されたものです。 同じプログラムはこのセクションの後に引用される結果でも使われています。。
ネットワークはランダムに初期化されていたので、ニューロンの学習速度のバラつきがあるのには驚きません。 しかし一つ気になるのは、2個目の隠れ層のバーが1個目の隠れ層のバーより遥かに大きい点です。 つまり、2個目の隠れ層は1個目の隠れ層よりも高速に学習するということのようです。 これは単なる偶然でしょうか、それとも一般的に2個目の隠れ層は1個目の隠れ層よりも速く学習するものなのでしょうか?
これが本当かどうか調べるために、一般的な方法で1層目と2層目の学習速度を比較してみます。 このために、勾配を $\delta^l_j = \partial C / \partial b^l_j$ とします。 これは $l$ 層目の中の $j$ 個目のニューロンの勾配*です *2章を振り返ると、これを誤差と呼んでいました。 しかし、ここでは「勾配」という非公式な呼び方を採用します。 「非公式」と言っているのは、もちろんこの式が、コスト関数の重みに関する偏微分 $\partial C / \partial w$ を明示的に含んでいないからです。。 勾配 $\delta^1$ は1個目の隠れ層の学習速度を定めるベクトルとしてみなすことができ、 $\delta^2$ は2個目の隠れ層の学習速度を定めるベクトルとみなせます。 これらのベクトルの長さを、層の学習速度の一般的な尺度(大ざっぱ!)として使いましょう。 したがってたとえば、長さ $\| \delta^1 \|$ は1層目の隠れ層の学習速度を示し、一方で、長さ $\| \delta^2 \|$ は2層目の隠れ層の学習速度を示すこととします。
これらの定義に従って、上図の設定のときの値を確認すると、 $\| \delta^1 \| = 0.07\ldots$ であり $\| \delta^2 \| = 0.31\ldots$ です。 したがって、先程の疑いを確かめたことになります。実際に、2個目の隠れ層のニューロンは、1個目の隠れ層のニューロンよりも遥かに速く学習していたのです。
隠れ層をさらに追加したとしたら、何が起こるでしょうか? もし、隠れ層が3個となったときには、各層での学習速度は 0.012、0.060、そして 0.283となります。 やはり、前方の隠れ層の学習は、後方の隠れ層よりかなり遅くなっています。 さらに30個のニューロンを持つ隠れ層を追加してみます。 この場合には、各層での学習速度は、0.003、0.017、0.070、そして0.285となります。 パターンとしては同じです。前方の層は後方の層よりも遅く学習しています。
これまでは訓練開始頃、すなわちネットワーク初期化直後の学習速度を見てきました。 ネットワークの訓練が進むと、学習率はどのように変化するのでしょうか? 2個の隠れ層のみ持つネットワークに立ち戻って確認してみましょう。 学習速度は次のように変化します。
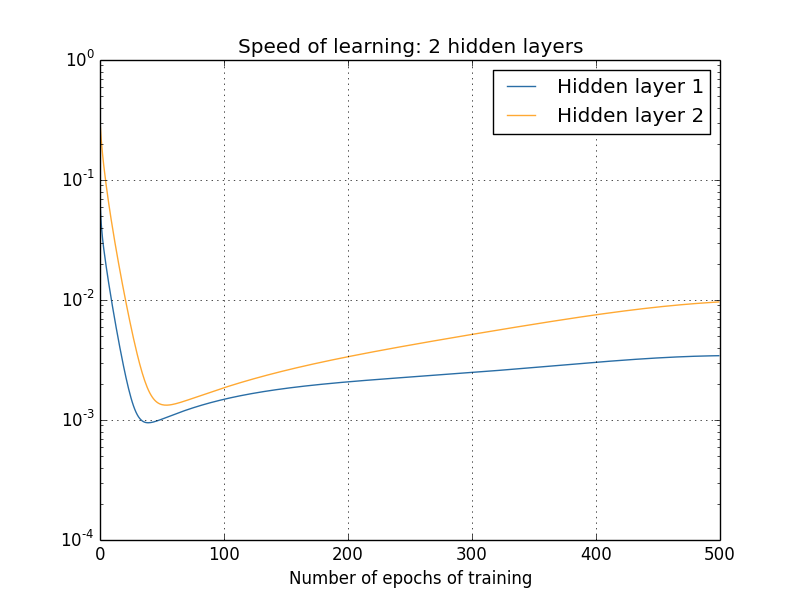
この結果を生成するために、1000個の訓練画像に対して、バッチ勾配降下を500エポックに渡り行いました。 これは通常の訓練方法と少し異なります。 ミニバッチを使わずに、しかも50000の訓練画像全体ではなく、たった1000の訓練画像のみを使ったからです。 もちろん卑怯な方法を使ったわけでも、あなたの目をくらまそうとしたつもりもありません。 ミニバッチ確率的勾配降下法を使うと、ノイズが混じった結果となってしまうのです(ノイズを平均化すればとても似た結果になりますが)。 私が選んだパラメータを使った方が、結果を簡単に滑らかにできるため、何が起きてるか見やすくなるはずです。
(既に知っているとおり、)2つの層が大きく異なる速度で学習し始めているのがわかります。 そして、どちらの層も急速に減少し、リバウンドします。 しかし全体的に、1個目の隠れ層は、2個目の隠れ層よりもゆっくり学習していると言えます。
もっと複雑なネットワークの場合はどうなるでしょうか? 次の図は、3個の隠れ層 $[784, 30, 30, 30, 10]$ を持つネットワークの場合の実験結果です。
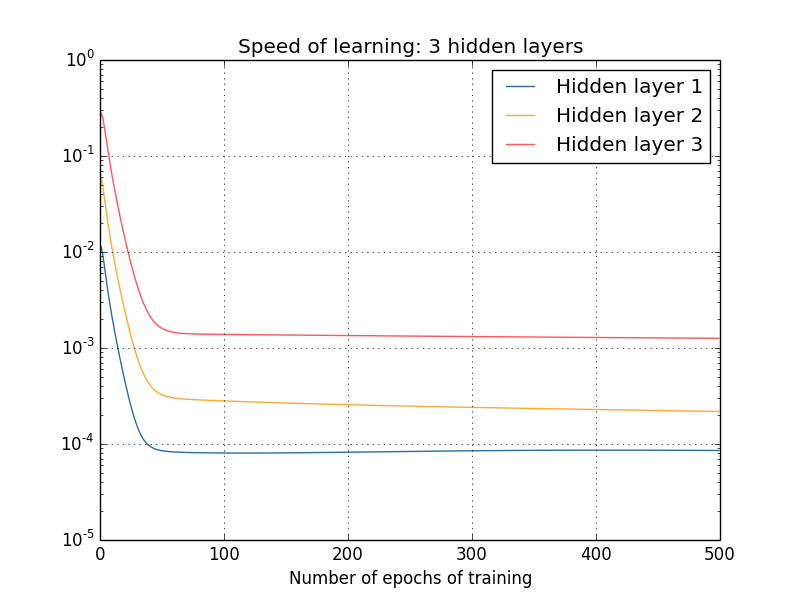
今回も、前方の隠れ層は後方の隠れ層より遅くなっています。 最後に、4個目の隠れ層を追加し( $[784, 30, 30, 30, 30, 10]$ のネットワークとして)、訓練時に何が起きるか見ましょう。
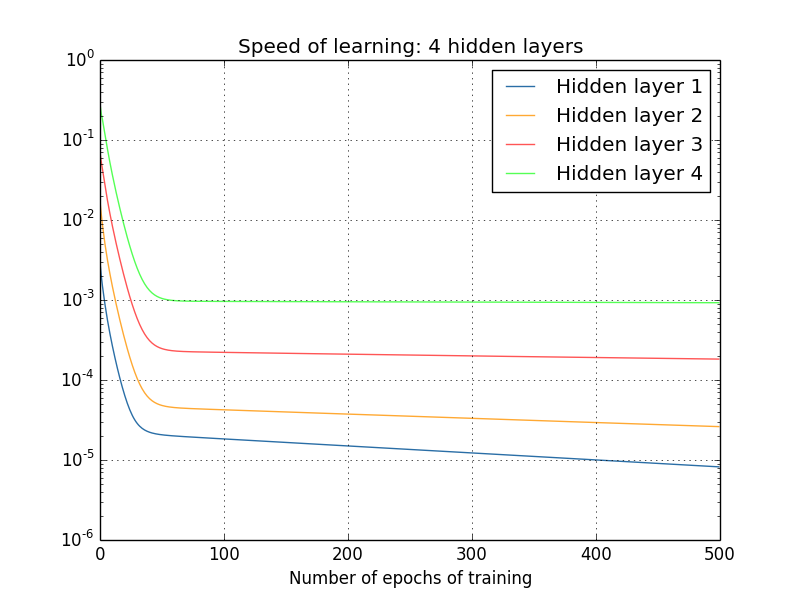
またもや、前方の隠れ層は後方のものよりも遅くなりました。 今回、最初の隠れ層は、最後の隠れ層よりも約100倍遅いという結果になっています。 前方のネットワークを訓練する難しさがわかったことでしょう!
私たちは重要な現象を観察しています。少しでも深いニューラルネットワークでは、 勾配は隠れ層を前方に伝わるにつれて小さくなる傾向があります。 これにより、前方の層のニューロンの学習は、後方の層のニューロンよりも遥かに遅くなります。 この現象をたった1つのネットワークの例で確認しましたが、実は多くのニューラルネットワークにおいて、同様の現象が発生する根源的な理由があります。 これは勾配消失問題*として有名な現象です *Gradient flow in recurrent nets: the difficulty of learning long-term dependencies, by Sepp Hochreiter, Yoshua Bengio, Paolo Frasconi, and Jürgen Schmidhuber (2001)を確認してください。 この論文はrecurrent neural networkを扱ったものですが、私たちの調べている順伝播ネットワークと本質的な現象は同じです。 Sepp Hochreiterの学位論文、 Untersuchungen zu dynamischen neuronalen Netzen (1991, in German)についても見てください。
なぜ勾配消失問題が起きるのでしょうか? この問題を避けられる方法はあるのでしょうか? 深いニューラルネットを訓練するときにどう対処すべきなのでしょうか? 実は、代替策がなくもないということをすぐに学びます。 しかしその代替策はそこまで魅力的なものではありません。 勾配が前方の層でかなり大きくなってしまう、という現象がしばしば発生してしまうのです! これは勾配爆発問題と言い、勾配消失問題と同じく悩ましい問題です。 一般的には、深いニューラルネットワークにおける勾配は不安定であり、前方の層で爆発もしくは消失する傾向があります。 この不安定性は、深いニューラルネットワークを勾配を利用して訓練するときの重大な問題です。 この問題は理解する必要があり、もし可能であれば、対処する手を打たなくてはいけません。
勾配消失(もしくは勾配の不安定性)への1つの反応は、本当にそれが問題になるのかと疑問に思うことです。 ニューラルネットから一瞬離れて、ある1変数関数 $f(x)$ を数値的に最小化することを考えてみましょう。 微分 $f'(x)$ が小さいことは良い知らせではないでしょうか? 既に極値に近づいていることを意味しているのではないでしょうか? こんな風に考えると、深いネットワークの前方の層での勾配が小さいということは、重みとバイアスをこれ以上調整する必要が無いことを意味しているのではないのでしょうか?
もちろん、これらの考えは間違っています。 ネットワークの重みとバイアスをランダムに初期化したことを思い出してください。 どんなネットワークであっても、重みとバイアスの初期値がいい感じになっているなんて、ありえないことです。 具体的に確認するために、MNIST問題用の $[784, 30, 30, 30, 10]$ のネットワークにおける最初の層の重みを考えてみます。 ランダムに初期化するということは、最初の層は、入力画像についての情報を捨てているということです。 たとえ、後方の層が素晴らしく訓練されていたとしても、後方の層からは入力画像を同定することができない状況となるのです。 なので、最初の層での学習は必要です。 深いネットワークを訓練する場合には、この勾配消失問題にどう取り組むべきかを明らかにする必要があります。
勾配消失問題の原因とは? 深いニューラルネットにおける不安定な勾配
なぜ勾配消失問題が起きるかを考察するために、 一番シンプルな深層ニューラルネットワークを考えます。 それは各層にただ1つニューロンをもつネットワークです。 下図のネットワークは3つの隠れ層を持ちます。

ここで、 $w_1, w_2, \ldots$ は重み、 $b_1, b_2, \ldots$ はバイアス、 $C$ はコスト関数です。 $j$ 番目のニューロンの出力 $a_j$ は $\sigma(z_j)$ とします。 $\sigma$ はいつもの シグモイドの活性化関数です。 $z_j = w_{j} a_{j-1}+b_j$ はニューロンへの入力に重みを施したものです。 コスト関数 $C$ は、ネットワーク全体の出力 $a_4$ のコストを表すことを強調しておきます。 もしネットワークの実際の出力が目標に近かった場合、コストは小さくなり、 一方、実際の出力が目標とかけ離れていれば、コストは高くなります。
1個目の隠れ層のニューロンに関連する勾配 $\partial C / \partial b_1$ について私たちは学んでいきます。 $\partial C / \partial b_1$ の式を学ぶことで、勾配消失問題がなぜ起きるかを理解したいと思います。
まず $\partial C / \partial b_1$ の式を見てみましょう。 とっつきにくく見えますが、実際にはシンプルな構造をしています。 すぐに解きほぐしていきます。 これが数式です(とりあえず、ネットワークは無視してください。$\sigma'$ は $\sigma$ のただの導関数です)

式の構造は次のようになっています。 $\sigma'(z_j)$ の項が各ニューロンに相当する積の中に現れています。 重み $w_j$ の項はネットワークの各重みに対応します。 そして、最後の項 $\partial C / \partial a_4$ はコスト関数に対応します。 上に挙げた項が、それぞれ対応するネットワーク部分の上に置かれていることを確認してください。 つまり、ネットワークはそれ自体が、数式の疑似表現になっているのです。
この数式を当たり前にとらえて、勾配消失問題とどう関係するのかの議論へ進んでも構いません。 そうして問題はありません。 なぜならこの数式は、先の逆伝播の議論における特別な場合であるからです。 でも、なぜこの数式が成り立つのかには簡潔な説明が可能であって、その説明を理解するのも面白い(ですし、加えてたぶん知恵もつくはず)です。
バイアス $b_1$ の微小な変化 $\Delta b_1$ を想像してみてください。 その変化が、残りのネットワークへカスケード的な変化を引き起こしていくでしょう。 まず第一に、1個目の隠れ層のニューロンの出力の変化 $\Delta a_1$ を起こします。 それが今度は、2個目の隠れ層への重み付き入力の変化 $\Delta z_2$ を起こします。 さらに、2個目の隠れ層からの出力 $\Delta a_2$ も変化します。 そうして、出力でのコスト $\Delta C$ まではるばる変化していくのです。 \begin{eqnarray} \frac{\partial C}{\partial b_1} \approx \frac{\Delta C}{\Delta b_1}. \tag{114}\end{eqnarray} このことは、カスケードの各ステップの影響を注意深く辿っていくことで、最終的に $\partial C / \partial b_1$ がわかることを示しています。
これを行うために、 $\Delta b_1$ がどのように1個目の隠れ層の出力 $a_1$ を変化させるのか考えてみましょう。 $a_1 = \sigma(z_1) = \sigma(w_1 a_0 + b_1)$ という式があるので、以下のようになります。 \begin{eqnarray} \Delta a_1 & \approx & \frac{\partial \sigma(w_1 a_0+b_1)}{\partial b_1} \Delta b_1 \tag{115}\\ & = & \sigma'(z_1) \Delta b_1. \tag{116}\end{eqnarray} $\sigma'(z_1)$ の項は馴染みがあるはずです。 勾配 $\partial C / \partial b_1$ の式中の最初の項でした。 直感的には、この項はバイアスの変化 $\Delta b_1$ を出力の活性の変化 $\Delta a_1$ へと変換します。 $\Delta a_1$ の変化は、今度は重みの付与された入力 $z_2 = w_2 a_1 + b_2$ として2個目の隠れ層へ伝わります。 \begin{eqnarray} \Delta z_2 & \approx & \frac{\partial z_2}{\partial a_1} \Delta a_1 \tag{117}\\ & = & w_2 \Delta a_1. \tag{118}\end{eqnarray} $\Delta z_2$ と $\Delta a_1$ の式を組み合わせると、バイアス $b_1$ の変化がネットワークをどう伝わって $z_2$ へ影響を及ぼすのかがわかります。 \begin{eqnarray} \Delta z_2 & \approx & \sigma'(z_1) w_2 \Delta b_1. \tag{119}\end{eqnarray} 再び馴染みのある式が現れました。 勾配 $\partial C / \partial b_1$ の式の最初の2つの項です。
このやり方で進めて、変化が残りのネットワークを伝播するのを追いかけていきます。 各ニューロンで $\sigma'(z_j)$ の項と、各重みごとに $w_j$ の項が現れます。 最終結果は、最初のバイアスの変化 $\Delta b_1$ に対する、最後のコスト関数の変化 $\Delta C$ の式となります。 \begin{eqnarray} \Delta C & \approx & \sigma'(z_1) w_2 \sigma'(z_2) \ldots \sigma'(z_4) \frac{\partial C}{\partial a_4} \Delta b_1. \tag{120}\end{eqnarray} $\Delta b_1$ で割ることで、本当に欲しい勾配を手に入れます。 \begin{eqnarray} \frac{\partial C}{\partial b_1} = \sigma'(z_1) w_2 \sigma'(z_2) \ldots \sigma'(z_4) \frac{\partial C}{\partial a_4}. \tag{121}\end{eqnarray}
なぜ勾配消失問題が起きるのか: 勾配消失問題の要因を理解するために、勾配全体の式を書き出してみましょう。 \begin{eqnarray} \frac{\partial C}{\partial b_1} = \sigma'(z_1) \, w_2 \sigma'(z_2) \, w_3 \sigma'(z_3) \, w_4 \sigma'(z_4) \, \frac{\partial C}{\partial a_4}. \tag{122}\end{eqnarray} 最後の項以外は、$w_j \sigma'(z_j)$ の積の項からなります。 これらの積の項がどう振る舞うかを理解するために、 $\sigma'$ のプロットを見てみます。
この導関数は $\sigma'(0) = 1/4$ の地点で最大値に達します。 ところで、標準的な方法 でネットワークの重みを初期化する場合には、平均 $0$ かつ標準偏差 $1$ のガウス分布から重みを選びます。 このとき、重みは通常 $|w_j| < 1$ を満たします。 これらの考察を組み合わせると、 $w_j \sigma'(z_j)$ の項は通常 $|w_j \sigma'(z_j)| < 1/4$ を満足します。 そして、そのような項をいくつも掛けていくと、積は指数関数的に減少していく傾向があります。すなわち、項が多くなればなるほど、積は小さくなっていきます。 上記は勾配消失問題の説明として妥当な気がします。
この説明をもう少し明確化するために、 $\partial C / \partial b_1$ の式を、後方の層のバイアスの勾配 $\partial C / \partial b_3$ と比べてみましょう。もちろん、まだ $\partial C / \partial b_3$ の式は計算してないのですが、 $\partial C / \partial b_1$ の上述のパターンと同じになります。こちらが2つの式の比較です。
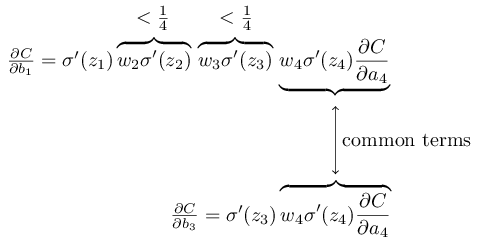
もちろん、これは大雑把な議論であり、勾配消失問題の発生に関する厳格な証明ではありません。 幾つかの例外事項もあります。 特に、重み $w_j$ が訓練中どんどん大きくなる可能性については気になることでしょう。 その場合、積の中の $w_j \sigma'(z_j)$ はもはや $|w_j \sigma'(z_j)| < 1/4$ を満たさなくなります。 実際にこの項が十分大きくなったとしたら、つまり $1$ より大きくなったら、勾配消失問題はなくなるでしょう。 代わりに、勾配は層を逆伝播するごとに指数関数的に大きくなっていきます。 勾配消失問題の代わりに、勾配爆発問題が起きるのです。
勾配爆発問題: 勾配爆発の起きる典型的な例を見てみましょう。 この例は恣意的なもので、勾配爆発が確実に起きるように、ネットワークのパラメータを修正していきます。 例として恣意的ではありますが、勾配爆発は仮説上の現象ではなく、実際に十分起きうるものです。
勾配爆発を引き起こすまでには、ステップが2つあります。 1つ目は、ネットワークの中の全ての重みを大きくしておくことです。 たとえば、 $w_1 = w_2 = w_3 = w_4 = 100$ とします。 2つ目のステップは、$\sigma'(z_j)$ の項があまり小さくなりすぎないように、バイアスを選ぶことです。 実際の操作は簡単です。 私たちが行うべきのは、各ニューロンへの重み付けされた入力が $z_j = 0$ を、(そして $\sigma'(z_j) = 1/4$ を) 満たすようにすることです。 したがって、たとえば、$z_1 = w_1 a_0 + b_1 = 0$ を得たいとしましょう。 私たちは $b_1 = -100 * a_0$ と設定することで上記を実現できます。 同じアイデアを、他のバイアスを選ぶときにも使えます。 このとき、全ての $w_j \sigma'(z_j)$ の項は $100 * \frac{1}{4} = 25$ に等しいことを確認しておきます。 これらの選択により、勾配爆発を起こせるのです。
不安定勾配問題: ここでの根本的な問題は、勾配消失問題でも、勾配爆発問題でもありません。 前方の層の勾配が、それ以降の層の勾配の積となっていることが問題なのです。 多層の場合、本質的に不安定な状況となります。 全部の層がほぼ同じ速度で学ぶ唯一の方法は、それらの項の積をほぼバランスさせることです。 バランスさせるための仕組みや要因が何もないとき、偶然には上手く行きようがありません。 つまり本当の問題は、ニューラルネットワークが 不安定勾配問題 を伴っていることです。 結果的に、勾配を利用する標準の学習テクニックを使うときには、ネットワーク中の異なる層は、かなり異なる速度で学習する傾向があります。
演習
- 勾配消失問題の議論の中で、 $|\sigma'(z)| < 1/4$ である事実を利用しました。別の活性化関数を使ったと想定し、その導関数はとても大きくなってしまったとします。その場合、勾配不安定問題は回避できるでしょうか?
勾配消失問題の広がり: これまでに、前方の層での勾配は消失するか爆発する可能性があることを見てきました。 実際、シグモイドのニューロンを使ったときには、勾配は通常、消失してしまうでしょう。 その理由については、 $|w \sigma'(z)|$ の式を再び考えてみてください。 勾配消失問題を避けるためには、 $|w \sigma'(z)| \geq 1$ とする必要があります。 もし $w$ がとても大きければ、上記は達成できると思っているでしょう。 しかし実際は、見た目よりずっと難しいのです。 その理由は、 $\sigma'(z)$ の項は $w$ にも依存していることにあります。 すなわち $a$ が活性化した入力とすると、 $\sigma'(z) = \sigma'(wa +b)$ となります。 だから、$w$ を大きくするときには、同時に $\sigma'(wa+b)$ を小さくしないよう注意する必要があります。 これは大きな制約です。 なぜかというと、 $w$ を大きくすると、$wa+b$ がとても大きく傾向があるからです。 $\sigma'$ のグラフの中では、 $\sigma'$ の「両翼」に相当する確率が高くなります。 そこではとても小さな値をとります。 これを避ける唯一の方法は、活性化された入力を、かなり狭い範囲の値(この定性的な説明は下記の定量的な説明により明らかです)に落ち着かせることです。 たまたま起きることはあります。 しかし、大抵は起きません。 したがって、一般的には勾配が消失してしまうのです。
問題
- 積 $|w \sigma'(wa+b)|$ を考えます。$|w
\sigma'(wa+b)| \geq 1$ とします。
(1) これが $|w| \geq 4$ の場合にだけ起こることを証明してください。
(2) $|w| \geq 4$ としたとき、
$|w \sigma'(wa+b)| \geq 1$ である入力の活性 $a$ を考えてください。この制約を満たす $a$ の組は、\begin{eqnarray}
\frac{2}{|w|} \ln\left( \frac{|w|(1+\sqrt{1-4/|w|})}{2}-1\right).
\tag{123}\end{eqnarray}
の幅より小さいインターバルに分布することを示してください。
(3) この範囲の幅の境界にある上式は $|w| \approx 6.9$ において最大値 $\approx 0.45$ をとることを示してください。
完璧に全てが並んだときでさえ、活性化された入力を狭い範囲で持てば、勾配消失問題を避けられるのです。
- Identity neuron: 1つの入力 $x$ 、重み $w_1$ 、バイアス $b$ 、出力への重み $w_2$ を持つニューロンを考えてください。 重みとバイアスを適切に選べば、 $x \in [0, 1]$ に対して $w_2 \sigma(w_1 x+b) \approx x$ が成り立つことを示してください。 そのようなニューロンはidentity neuronとして使えます。 それはすなわち、出力が入力と同じとなるニューロンのことです。 ヒント: $x = 1/2+\Delta$ を記述し、$w_1$ が小さいと想定し、 $w_1 \Delta$ のテイラー展開を使ってみてください。
さらに複雑なネットワークにおける不安定な勾配
これまで、各隠れ層に一つのニューロンだけ持つような、トイネットワークを使って勉強してきました。 もっと複雑な深層の、各隠れ層にたくさんのニューロンを持つようなネットワークの場合どうなるのでしょうか?
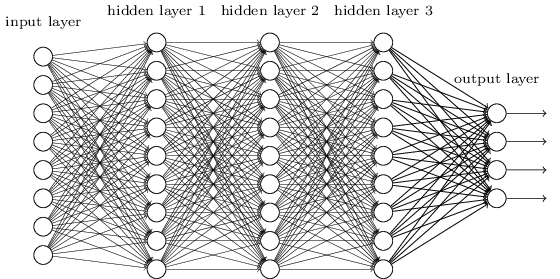
実際、そのようなネットワークにおいても、同じ振る舞いが見られます。 逆伝播の章で見たように、全 $L$ 層のネットワークの $l$ 層目 の勾配は次の式で 与えられます。
\begin{eqnarray} \delta^l = \Sigma'(z^l) (w^{l+1})^T \Sigma'(z^{l+1}) (w^{l+2})^T \ldots \Sigma'(z^L) \nabla_a C \tag{124}\end{eqnarray}
ここで、 $\Sigma'(z^l)$ は対角行列で、各成分は、 $l$ 層目に対する重み付き入力への $\sigma'(z)$ となります。 $w^l$ は異なる層に対する重み行列です。 $\nabla_a C$ は活性化された出力に対する $C$ の偏微分ベクトルです。
これは各層に1ニューロンの場合よりも遥かに複雑です。 でも、よく見ると、本質的な形状はとてもよく似ています。 $(w^j)^T \Sigma'(z^j)$ の項の組がたくさんあります。 加えて、行列 $\Sigma'(z^j)$ の対角成分は $\frac{1}{4}$ よりも小さくなります. もし、重み行列 $w^j$ がそこまで大きくない場合、 $(w^j)^T \Sigma'(z^l)$ の各項は勾配ベクトルを小さくする働きがあり、勾配消失問題が発生します。 一般的に言うと、先の例のように積の中に項が多くなると、勾配が不安定になります。 経験的には、シグモイドのネットワークにおいて、前方の層で勾配が急速に消失する現象が顕著に見られます。 結果的に、前方の層での学習は遅くなります。 学習が遅いことは、偶然でも単なる不都合でもありません。 学習のために私たちが採用した方法のもつ根本的な問題なのです。
ディープラーニングに関する他の問題
この章では、ディープラーニングの問題として勾配消失(や、もっと一般的には勾配の不安定性)に焦点を当ててきました。 勾配の不安定性は重要で本質的な問題ではありますが、実際にはディープラーニングの一つの問題に過ぎません。 現在も多くの研究が、深層ネットワークの訓練時に発生する難問を理解しようと試みています。 ここで包括的にまとめることはしませんが、いくつかの論文を簡単に紹介します。 人々が解決したいと思っている問題の雰囲気をあなたに届けたいと思います。
1つ目の例は、2010年にGlorotとBengio* *Understanding the difficulty of training deep feedforward neural networks, by Xavier Glorot and Yoshua Bengio (2010)。シグモイドの利用に関する先の議論である、Efficient BackProp, by Yann LeCun, Léon Bottou, Genevieve Orr and Klaus-Robert Müller (1998)も確認してください。 が、シグモイドを活性化関数に使うと、深いネットワークでの訓練時に問題が生じる証拠を発見した論文です。 特に、シグモイドが最後の隠れ層の活性化において、訓練の初期にほぼ $0$ に飽和して、実質的に学習を遅くさせる証拠を見つけています。 彼らは、この飽和の問題の発生しないような、代わりの活性化関数を提案しました。
2つ目の例として、2013年にSutskever、Martens、Dahl、Hinton* *On the importance of initialization and momentum in deep learning, by Ilya Sutskever, James Martens, George Dahl and Geoffrey Hinton (2013)。 を挙げます。 彼らはランダムな重みの初期化と、momentumに基づいた確率的勾配降下法のmomentumのスケジューリングによるディープラーニングへの影響を調べました。 どちらの場合にも、パラメータをうまく選択することで、深層ネットワークの訓練が成功しました。
これらの例が示唆するのは、 「深いネットワークを訓練するときの難しさは何か」というのは複雑な問いであるということです。 この章では、深いネットワークにおいて、勾配を利用する学習を行うときの不安定性に焦点を当ててきました。 直前の2つの段落での結果は、活性化関数の選択や、重みの初期化の仕方、さらに勾配降下の学習方法の実装によっても、学習の効果が変わってくることを示すものでした。 そしてもちろん、ネットワークの構造や他のハイパーパラメータの選択も重要です。 したがって、多くの要素が深いネットワークの訓練を難しくさせうるのです。 そしてこれらを全て理解するために、研究が現在も進められているのです。 このことは、暗澹としていて悲観的であるように思えます。 しかし、良い知らせもあります。 私たちは、次の章でこれらの問題をひっくり返します。 ある程度はこれらの難問を克服もしくは回避するような、ディープラーニングのアプローチを開発します。






