前章で、深いニューラルネットワークを訓練するのは、浅いネットワークを訓練する場合よりもずっと難しいことを学びました。 これは悲しいことです。 なぜなら、もし深いネットワークを上手く訓練できれば、浅いネットワークよりも遥かに強力になるからです。 前章の知らせは残念ですが、私たちは歩みを止めません。 この章では、深層ネットワークの訓練に使えるテクニックを発展させ、実践的な課題へ適用していきます。 また、深層ネットワークの幅広い応用例として、画像認識や音声認識などに関する最新結果を簡単に紹介します。 そして、ニューラルネットワークや人工知能の未来に何が待っているのか、についても予測していきます。
この章はとても長いです。 章の全体を軽く案内しましょう。 各セクション間の繋がりは強くはありません。 ですので、ニューラルネットワークに既に少し馴染みがあるなら、興味のあるセクションへ先に飛ぶのもよいでしょう。
この章の主要なテーマは、幅広く使われている深層ネットワークの一種である、深層畳み込みネットワークの紹介です。 MNISTの手書き数字の分類問題に対して、畳み込みネットワークを駆使して挑んで行く様子を、コードを交えながら詳細に追っていきます。
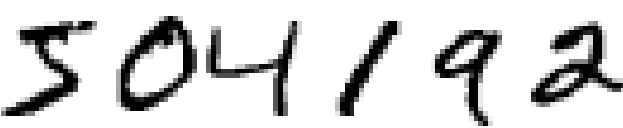
畳み込みネットワークの説明に際しては、 本書で扱ってきた浅いネットワークと比較しながら進めます。 試行錯誤により、ネットワークをいじりながら作り上げていきます。 その過程でたくさんの強力なテクニックを学ぶでしょう。 畳み込み、プーリング、(浅いネットワークの場合よりも効率的に訓練するための)GPUの使用、(過適合の抑制のための)訓練データの拡張、(過適合の抑制のための)ドロップアウト、ネットワークのアンサンブルなどを学んでいきます。 これらを組み合わせると最終的に、人間に近いパフォーマンスを出せるシステムが出来上がります。 10,000個のMNISTテスト画像(これらは訓練画像には含まれません!)から、9,967個を正しく分類できるようになります。 誤って分類した33個の画像をちらっと見てみましょう。 正しい分類が手書き数字の右上に表示されており、私たちのプログラムが分類した結果が右下に表示されています。

人間でも正しく分類するのは難しい画像が多いです。 例えば、上の行の3つ目の画像を見てください。 正解は"8"ですが、私には"8"よりは"9"に見えます。 私たちのネットワークも"9"と判断しています。 この類の"間違い"は許容できるもので、むしろこの間違いを犯せるのは立派ではないかとさえ思えます。 画像認識の議論のまとめとして、畳み込みネットワークを使用した最近の目まぐるしい研究成果を調査します。
この章の最後では、大局的にディープラーニングを概観します。 具体的には、再帰型ニューラルネットワーク(RNN)や長期短期記憶(LSTM)ユニットなどの他のニューラルネットワークのモデルを簡単に調査して、 そのようなモデルが音声認識や自然言語処理や他の分野の問題にどう適用可能であるのか考察します。 そして、意思だけで使えるユーザインターフェイスから、人工知能におけるディープラーニングの役割まで幅広く扱い、ニューラルネットワークとディープラーニングの未来を予測します。
この章は、本書のこれまでの章の内容の集大成です。 例えば、逆伝播、正規化、ソフトマックス関数などのアイデアを組み合わせてネットワークに利用します。 ですがこの章を読むのに、前章までを詳細に読み切る必要はありません。 ただし1章を読んで、ニューラルネットワークの基礎を抑えておくのは役に立つでしょう。 2章から5章までのアイデアを利用するときには、必要であれば飛べるようにリンクを表示します。
この章では扱わないトピックを明確化しておきます。 まず、ニューラルネットワークの素晴らしい最新ライブラリのチュートリアルではありません。 また、数十の深層ネットワークを、巨大な計算機を使って訓練することで最先端の問題を解く、というようなトピックも扱いません。 それよりむしろ、深層ニューラルネットワークの根源的な原理を理解することに焦点を当て、その原理をシンプルで理解しやすいMNISTの問題に適用します。 繰り返すと、この章を読んでも最先端の流行には辿り着けません。 しかし、この章と以前の全章を読むことであなたは深層ニューラルネットワークの本質に触れることができ、いずれは現在の流行を理解できるようになるでしょう。
畳み込みニューラルネットワークの導入
以前の章では、ニューラルネットワークの、手書き数字画像の認識精度を向上することを目的としていました。
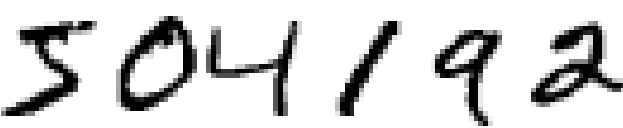
この目的のために、隣接層がお互いに全結合するネットワークを使用していました。 これは、ネットワーク内の全てのニューロンが、隣接する層の全てのニューロンと結合している状態です。
さらに、入力画像の各ピクセルの強度を、入力層内の対応するニューロンへエンコードしていました。 これはつまり、使用した $28 \times 28$ ピクセルの画像の場合、ネットワークは $784$ ($= 28 \times 28$) の入力ニューロンを持つということです。 そして、ネットワークの重みとバイアスを訓練することで、入力画像が'0', '1','2', ..., '8', '9'のいずれであるかを、ネットワークの出力から(望みどおり!)特定しようとしました。
これまで作ってきたネットワークは上手く動いていました。 MNISTの手書き数字データセットから取り出した訓練データとテストデータを使って、98%以上の分類精度を達成していたのを覚えているでしょうか。 しかしよく考えると、画像を分類するのに全結合層からなるネットワークを使うのは変です。 なぜかというと、全結合層からなるネットワークは、画像の空間的な構造を考慮していないからです。 たとえば全結合層では、入力ピクセルの中の離れたところにあるもの同士と、近いところにあるもの同士が全く同等に扱われます。 そのような空間的な構造の概念自体、全結合層のネットワークの場合、全て訓練データから推測されなければなりません。 しかし、真っさらな状態のネットワーク構造からスタートする代わりに、空間構造を活用したネットワーク構造を使ったとしたらどうでしょう? このセクションでは、畳み込みニューラルネットワークを扱います。 *畳み込みニューラルネットワークのはじまりは、1970年代まで遡ります。 しかし、近年の畳み込みニューラルネットワークブームの発端の論文は1998年のby Yann LeCun, Léon Bottou, Yoshua Bengio, Patrick Haffnerによる"Gradient-based learning applied to document recognition"です。 LeCunは畳み込みネットワークの用語定義に関して興味深い次のような発言を残しています。 「畳み込みネットワークのモデルは、生物学の神経モデルからはあまり着想を得ていません。そのため私は、"畳み込みニューラルネットワーク"ではなく"畳み込みネットワーク"と呼んでいます。そして、ノードに対しても"ニューロン"ではなく"ユニット"と呼んでいます」と。 この発言に反して、畳み込みネットワークは、私たちが学んできたニューラルネットワークと同じアイデアを多く利用しています。 例えば、逆伝播や勾配降下、正規化、非線形な活性化関数などです。 なので、慣例に従い、これからはニューラルネットワークの1種とみなします。 "畳み込みニューラルネットワーク"という用語と"畳込みネットワーク"という用語を同じ意味で使っていきます。 "(人工)ニューロン"や"ユニット"という用語も同義として使っていきます。 畳み込みネットワークは、空間的構造性を考慮した設計となっており、画像分類に非常に適しています。 この特性により、畳込みネットワークは効率的に学習できるのです。 つまり、画像を分類するのに優れた、深くて多層のネットワークを訓練できると言えます。 今日、深層の畳み込みネットワークもしくは類似のネットワークが、画像認識を目的とするニューラルネットワークの大半に使われています。
畳み込みニューラルネットワークは次の3つの重要なアイデアを使っています。 それは、局所受容野、重み共有、プーリングです。 各アイデアを順に見ていきましょう。
局所受容野: 上で確認した全結合層では、入力は一列のニューロンとして描かれていました。 一方、畳み込みネットワークでは、入力を $28 \times 28$ の正方形のニューロンと考えます。 各ニューロンの値は、入力として用いる $28 \times 28$ の入力ピクセルの強さに対応します。

いつも通り、入力のピクセルを隠れ層のニューロンに結合します。 しかし、隠れ層の各ニューロンへ、各入力ピクセルを結びつけることはしません。 代わりに、各ニューロンへ入力画像の中の小さい局所領域を結合します。
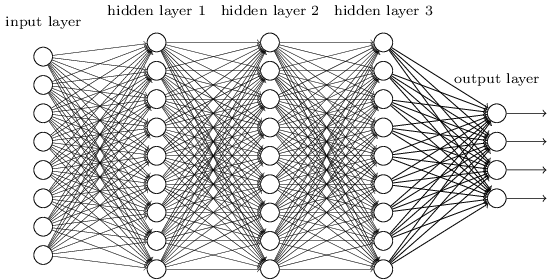
正確に言うと、1つ目の隠れ層の各ニューロンは、入力ニューロンの小さい領域と結合します。 例えば、入力の $25$ ピクセルに対応する $5 \times 5$ の領域に、隠れ層の各ニューロンが結合します。 ある隠れニューロン結合を示すと次のようになります。
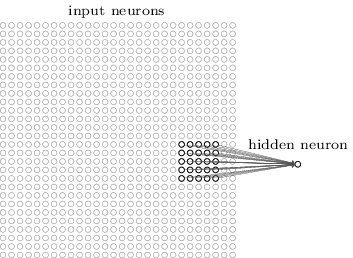
入力画像内のそのような領域は、隠れニューロンの局所受容野と呼ばれます。 入力ピクセル上の小さな窓のようなものです。 各結合は重みを学習します。 隠れニューロンはバイアスも同じく学習します。 特定の隠れニューロンは、特定の局所受容野を分析しているとみなせます。
そして、入力画像全体をカバーするように局所受容野をスライドさせます。 局所受容野ごとに、1つ目の隠れ層の中で異なる隠れニューロンが割り当てられます。 これを具体的に確認してみます。 左上の角の局所受容野から始めてみましょう。

1ピクセル分(すなわち1ニューロン分)局所受容野を右へスライドして、次は2つ目の隠れニューロンの結合を考えます。

これを繰り返して、最初の隠れ層の全体に対して値を設定します。 入力画像のサイズが $28 \times 28$ で、局所受容野のサイズが $5 \times 5$ の場合、1つ目の隠れ層のニューロンは $24 \times 24$ 個となります。 その理由は、入力画像の右側(もしくは下側)にぶつかるまでに、$23$ 個のニューロン分だけ局所受容野をスライドできるからです。
ここまで、$1$ ピクセルずつ局所受容野が移動する例を見てきました。 実は、ストライドの長さに $1$ 以外の値が使われることがしばしばあります。 たとえば、$2$ ピクセルずつ局所受容野を右へ(もしくは下へ)動かすこともあるでしょう。 これは、$2$ ピクセルのストライド長さが使われていると言えます。 この章では大抵、ストライドの長さが $1$ の場合しか扱いませんが、 時には異なるストライド長さ*が使用されて実験が行われる場合もあることは知っておいてください。 *以前の章で触れたように、異なるストライド長さを試したい場合、最適なパフォーマンスを発揮するストライド長さを決めるには、検証データを使うのがよいでしょう。 詳細は、ニューラルネットワークでハイパーパラメータを選ぶ方法についての以前の議論を確認してください。 同じアプローチが局所受容野のサイズを選ぶ時にも使われるでしょう。 もちろん、$5 \times 5$ の局所受容野を使う特別な理由はないのです。 一般的には、入力画像が $28 \times 28$ のMNIST画像よりもずっと大きい時には、大きいサイズの局所受容野を使って方が良い傾向があります。
重みとバイアスの共有: 各隠れニューロンはバイアスと局所受容野に結合された $5 \times 5$ の重みを持つことを上で述べました。 しかし、$24 \times 24$ の全ての隠れニューロンに対して、同じ重みとバイアスを適用することをまだ伝えていませんでした。 これはつまり、$j, k$ 個目の隠れニューロンへの出力は、下記のようになることを示しています。 \begin{eqnarray} \sigma\left(b + \sum_{l=0}^4 \sum_{m=0}^4 w_{l,m} a_{j+l, k+m} \right). \tag{125}\end{eqnarray} $\sigma$ は活性化関数の一種であり、以前の章で使用したシグモイド関数です。 $b$ はバイアスの共有値です。 $w_{l,m}$ は共有重みであり、そのサイズは $5 \times 5$ です。 そして、$a_{x, y}$ は $x, y$ における活性化された入力を示します。
このことが意味するのは、入力画像の異なる位置の全く同じ特徴*を、1層目の隠れ層が検知するということです。 *まだ特徴の厳密な定義をしていませんでした。 砕けた言い方をすると、隠れニューロンに検知される特徴とは、ニューロンを活性化する入力パターンの種類を意味します。 そのパターンとは例えば、画像のエッジだったり他の形状だったりします。 なぜこれが成り立つのかを理解するために、 隠れニューロンが縦のエッジを局所受容野に検知できるような、重みやバイアスを想定してみてください。 この検知能力は、画像の他の位置でも有効に使えそうです。 したがって、同じ特徴検出器を画像の全位置へ適用するのは有効と言えるのです。 少し抽象的に表現すると、畳込みニューラルネットワークは画像に対して並進不変性があると言います。 並進不変性とは例えば、猫の絵を少し並進移動しても、それはまだ猫の絵と言えるような性質のことです* *私たちが勉強してきたMNIST手書き数字の分類問題では、画像は中央に寄っており、大きさが正規化されていました。 なので、MNISTは世の中にある画像よりも、並進不変性が小さいと言える。 しかしそれでも、エッジや角といった特徴は入力空間全体において有効に使えるでしょう。
この理由から、入力層から隠れ層への写像を特徴マップと呼ぶこともあります。 特徴マップを定義する重みを共有重みと呼びます。 また、特徴マップを同じように定義するバイアスを、同じように共有バイアスと呼びます。 共有重みと共有バイアスはしばしば、カーネル、もしくはフィルタと呼ばれます。 文献では、これらの用語を少し異なる使い方をする場合があります。 そのため、私は用語の正確性は放棄しています。 むしろ具体例で確認することのほうが本質的なので、そのように心がけていきます。
これまで扱ってきたネットワーク構造は、一種類の局所的特徴のみ検知できるものでした。 画像認識のためには、二つ以上の特徴マップが必要となります。 したがって、完全な畳込み層は幾つかの異なる特徴マップから構成されるのです。
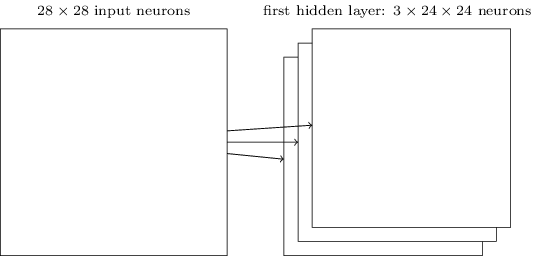
図をシンプルにするために、 $3$ つの特徴マップだけを見せました。 しかし、実際の畳み込みネットワークは(たぶん遥かに)多くの特徴マップを使っているかもしれません。 初期の畳み込みネットワークであるLeNet-5は、MNISTの手書き数字を認識するために $6$ つの特徴マップを使っていました。 各特徴マップは $5 \times 5$ の局所受容野と結合しています。 したがって、上記の例はLeNet-5と実際かなり近いのです。 章の後ろの方で開発するネットワークでは、 $20$ と $40$ の特徴マップをそれぞれ持つ畳み込み層を使っています。 その特徴マップを少し覗き見してみましょう* *図の特徴マップは私たちが訓練する最後の畳み込みネットワークに含まれるものです。ここを確認してください。

$20$ 個の画像は $20$ 個の異なる特徴マップ(もしくはフィルタかカーネル)に対応しています。 各マップは、 $5 \times 5$ ブロック画像で表され、局所受容野の $5 \times 5$ の重みに対応しています。 白いブロックは小さい(概してマイナスの)重みを意味し、その特徴マップは入力ピクセルに反応しにくいという性質を持ちます。 一方、黒いブロックは大きい重みを意味し、その特徴マップは入力ピクセルによく反応します。 大まかに言うと、畳み込み層がどのような種類の特徴に反応するかを、上の画像群は示しています。
これらの特徴マップからどんな結論を導けるでしょうか? 何らかの空間的構造が特徴マップには現れているようです。 特徴マップの多くは明るい領域と暗い領域の両方を含んでいます。 これにより、空間的構造に関する特徴をネットワークが学習していることが分かります。 しかし、これらの特徴検出器が何を学んでいるのかを、それ以上に深く把握するのは難しいです。 明らかに、この特徴は画像認識の伝統的なアプローチでたくさん採用されてきたガボールフィルタではありません。 畳み込みネットワークの学習した特徴を、突き詰めて理解しようとする研究が、現在多数進行中です。 もし興味があるのなら、2013年のMatthew ZeilerとRob FergusによるVisualizing and Understanding Convolutional Networksを読むのを薦めます。
重みとバイアスを共有する大きな利点は、畳込みネットワークのパラメータ数を大きく減らせる点です。 上記の畳み込みネットワークのパラメータを数えてみます。 特徴マップごとに $25 = 5 \times 5$ の共有重みと、1つの共有バイアスを必要とします。 つまり、各特徴マップは $26$ のパラメータが必要です。 $20$ 個の特徴マップがある場合には、畳込み層を定義するための全パラメータは $20 \times 26 = 520$ 個となります。 それと比較するために、全結合層のパラメータ数を数えてみます。 これまで本書で使ってきた例と同様に $784 = 28 \times 28$ 個のニューロンからなる入力層と、$30$ 個の隠れニューロンからなる全結合層で構成されるネットワークを仮定してみてください。 その場合、 $784 \times 30$ 個の重みとさらに $30$ 個のバイアスで、全部で $23,550$ 個のパラメータからなります。 つまり、全結合層は畳み込み層と比べて $40$ 倍のパラメータを保持することになるのです。
もちろん、根本的に2つのモデルは異なっているため、パラメータ数を直接比較することは本当はできません。 しかし直感的に考えてみても、畳み込み層には並進不変の性質があるので、全結合層のモデルと同じパフォーマンスを得るのに要するパラメータ数は少なくなると思えます。 パラメータ数が小さいおかげで、畳込みモデルは高速に訓練でき、層を深くできるのです。
ところで、畳み込みという呼び名は(125)の、畳み込みという名で知られた操作に由来しています。 正確に式を記述すると、$a^1 = \sigma(b + w * a^0)$ となります。 ここで、 $a^1$ はある特徴マップからの活性化された出力、$a^0$ は活性化された入力、$*$ は畳み込みと呼ばれる操作を示します。 私たちは、いわゆる数学における畳込み操作を深く追い求めません。 なので、数学との結びつきを心配する必要はありません。 しかし、由来が何なのかは少なくとも知っておいて損はありません。
プーリング層: 通常の畳み込みニューラルネットワークは、先ほどの畳み込み層に加えて、プーリング層も含みます。 このプーリング層は通常、畳込み層の直後に置かれます。 この層の役割は畳込み層の出力を単純化することです。
少し詳しく説明すると、プーリング層は畳み込み層から各特徴マップ*を取得し、特徴マップを濃縮させています。 *ここでの用語の定義ははっきりしていません。 私は「特徴マップ」という言葉を、畳み込み層から算出される関数を指して使うのではなく、活性化された出力ニューロンのことを指して使います。 この類の意味の揺れは、研究論文によくあることです。 つまり、プーリング層の各ユニットは前層の $2 \times 2$ の領域のニューロンをまとめます。 具体的な手法を紹介すると、プーリングのよく知られた例としてMaxプーリングがあります。 Maxプーリングでは、プーリングのユニットは $2 \times 2$ の入力領域のうちで最大の値を単純に出力します。 次の図を見てください。

畳み込み層の出力ニューロンは $24 \times 24$ なので、プーリング処理後は $12 \times 12$ のサイズのニューロンとなります。
上で述べた通り、畳み込み層は通常1つ以上の特徴マップを持ちます。 それらの特徴マップに対して個別にMaxプーリングを適用します。 したがって、3つ特徴マップがある場合には、畳込み層とMaxプーリング層の様子は次のようになります。
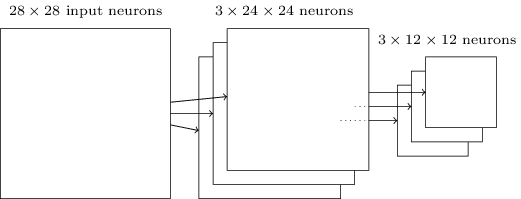
Maxプーリングは、画像のある領域内のどこかに指定の特徴があるかをネットワークが確認する手段とみなせます。 つまり正確な位置の情報は棄てているのです。 直感的に解釈すると、一度特徴が見つかればその正確な位置は重要でなく、他の特徴に対するおおよその位置さえ分かればよいということなのです。 この手法の大きな利点は、特徴はプーリングされると少なくなるため、後方の層で必要なパラメータを減らすことができる点です。
プーリングの手法はMaxプーリングだけではありません。 他のよく知られたアプローチとしてL2 プーリングがあります。 L2プーリングの手法では、 $2 \times 2$ 領域のニューロンの活性化出力の最大値をとるのではなく、 $2 \times 2$ 領域の活性化出力の和の平方根をとります。 L2プーリングは、畳み込み層からの情報を圧縮する方法とも言えます。 詳細な手続きは異なるものの、直感的にはMaxプーリングに近いはたらきをします。 実際、どちらの手法も広く使われてきました。 そして、場合によってはさらに別のプーリング手法も使われることもあります。 パフォーマンスを本気で良くしようと思ったら、検証データを使って異なるプーリング手法を試すのが良いでしょう。 そして、一番良い手法を選択するのです。 しかし私たちは、細かい最適化の種類を気にかけるつもりはありません。
全てを1つにまとめる: さあ、これまでのアイデアを全て使って、畳み込みニューラルネットワークを完成させましょう。 これから作るものは、上で見てきた構造と似ていますが、$10$ のニューロンを持つ出力層が追加されています。 この層の各ニューロンはMNISTの $10$ 種の手書き数字 ('0', '1', '2', etc) に対応するものです。
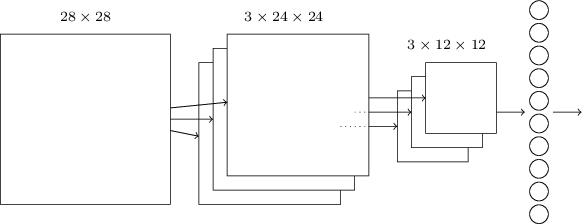
このネットワークは、MNIST画像のピクセル強度を符号化するのに使われる $28 \times 28$ の入力ニューロンから始まります。 そして、$5 \times 5$ の局所受容野と $3$ の特徴マップを使う畳み込み層が続きます。 この畳み込み層は $3 \times 24 \times 24$ の隠れ特徴ニューロンから構成されます。 次にMaxプーリング層が続きます。 この層では $2 \times 2$ の領域を $3$ の特徴マップごとに処理します。 つまりプーリング層は $3 \times 12 \times 12$ の隠れ特徴ニューロンからなります。
ネットワークの最後の層は全結合層です。 Maxプーリング層の全てのニューロンと この層の $10$ の出力ニューロンが個別に結合します。 この全結合の構造は以前の章で扱ったものと同じです。 しかし、上図では表記をシンプルにするため、全ての結合を表示する代わりに1つの矢印で表現しています。 結合の様子は容易に想像できるでしょう。
この畳込み構造は、以前までの章で扱ってきた構造と大きく異なります。 しかし、全体像は似ています。 ネットワークは単純なユニットから構成され、各ユニットの振る舞いは重みとバイアスから決定されます。 全体の目標も同じです。 それは、訓練データによりネットワークの重みとバイアスを訓練して、ネットワークが入力画像を上手く分類できるようにすることです。
また、以前の章と同じようにネットワークの訓練には、確率的勾配降下法と逆伝播を用います。 以前の章と殆ど同じです。 しかし、逆伝播の手続きには、少し修正を加える必要があります。 以前の章の逆伝播による偏微分導出では、全結合層を対象とした手続きを扱っていたためです。 幸運なことに、畳込み層とMaxプーリング層の偏微分の式を導出するには、修正を少し加えるだけで済みます。 もし詳細を理解したければ、次の問題に取り組んだほうがよいでしょう。 ただし、逆伝播にる前方の層の偏微分を正しく理解していない限り、この問題を解くには少し時間がかかります。
問題
- 畳み込みネットワークにおける逆伝播: 全結合層のネットワークにおける逆伝播の重要な式は (BP1)-(BP4) (link)でした。 上述のネットワークのように、畳み込み層、Maxプーリング層、全結合の出力層から構成されるネットワークを想定してください。 この時、逆伝播の式はどのように修正されるでしょうか?
畳み込みニューラルネットワークの実際
畳み込みニューラルネットワークの核となるアイデアをこれまで確認してきました。 実際にそれらがどう作用するのかを、畳込みネットワークを実装し、MNISTの数字分類問題へ適用することで確認してみましょう。 今回、私たちが使うプログラムはnetwork3.pyです。 これは以前の章で使ったnetwork.pyとnetwork2.pyの改良版です* *network3.pyはTheanoライブラリの畳み込みニューラルネットワークのドキュメントからアイデアを取り込んでいることにも注意してください (特にLeNet-5の実装部分) 。 また、Misha Denilの ドロップアウトの実装や、 Chris Olahのアイデアも参照しています。。 コードを参照したい場合、GitHubからコードを取得できます。 次のセクションではnetwork3.pyを作り上げていきます。 一方、このセクションでは、network3.pyを畳み込みネットワークを構築するためのライブラリとして使います。
network.pyとnetwork2.pyはPythonと行列ライブラリであるNumpyを使って実装されていました。 その際、ニューラルネットの原理や逆伝播、確率的勾配降下法などを学ぶために、各実装をスクラッチから行いました。 しかし、これらの詳細を私たちは既に理解しているため、network3.pyではTheano*という機械学習ライブラリを利用します *2010年のJames Bergstra, Olivier Breuleux, Frederic Bastien, Pascal Lamblin, Ravzan Pascanu, Guillaume Desjardins, Joseph Turian, David Warde-Farley, and Yoshua BengioによるTheano: A CPU and GPU Math Expression Compiler in Pythonを確認してください。 Theanoは、人気のあるPylearn2や Kerasなどのニューラルネットワークライブラリにも利用されています。 この本の執筆中の現在、他の人気のニューラルネットライブラリには、 Caffeと Torchがあります。 Theanoを使うことで、畳み込みニューラルネットワークでの逆伝播を簡単に実装できます。 それは全ての結合での計算を自動的に行ってくれるためです。 さらにTheanoは私たちの以前のコード(こちらは速度よりも理解しやすさを重視して記述されています)よりも高速であり 、複雑なネットワークを訓練するにはとても実用的です。 Theanoのさらに別の利点は、1つのコードをCPU上でもGPU上でも実行できることです。 GPU実行により高速化が実現されるため、複雑なネットワークの利用に実用性が生まれます。
コードを追いたい場合には、あなたのシステムでTheanoを実行する必要があります。 Theanoのインストールは、プロジェクトページの指示に従い行ってください。 以降のコードはTheano 0.6*で実行を確かめています *この章を公開時には、Theanoの最新バージョンは0.7に更新されていました。 Theano 0.7でも同じコードを実行してみたところ、本書の記載結果とほぼ同等の結果が得られました。 。 コードの一部はGPUなしのMac OS X Yosemiteで実行しました。 また、一部はNVIDIAのGPUありのUbuntu 14.04の環境で実行しました。 幾つかの実験はどちらの環境でも試しました。 network3.pyの実行の際は、network3.pyのコード中のGPUフラグをTrueかFalseのどちらか適当な方に設定する必要があります。 Theanoを起動してGPU上で動かす際には、このインストラクションが役立ちます。 ウェブ上のチュートリアルもGoogle検索により簡単に見つかります。 きっと、あなたの助けになるでしょう。 ローカル環境でGPUを利用できない場合、Amazon Web Servicesの EC2インスタンスやG2インスタンスを試すとよいでしょう。 ただしGPUを使ったとしても、処理に時間がかかるコードがあることに注意してください。 実験の多くは数分から数時間かかります。 一番複雑な実験は、CPUだと数日かかるでしょう。 以前の章でお薦めしたように、コードを実行している間に本書を読み進めて、時たま出力結果を確認するのが良いと思います。 CPU上で複雑な実験を行う際には、訓練のエポック数を小さくするか、実験そのものを諦めた方がよいでしょう。
準備運動として、
$100$のニューロンを含む隠れ層を1つだけを持つ浅いネットワークから始めてみましょう。
訓練のエポック数は $60$ 、学習率は $\eta = 0.1$、ミニバッチサイズは $10$、正規化なしの条件で実行してみます*。
*このセクションの実験用コードは
このスクリプトの中にあります。
スクリプト中のコードは、このセクションの議論に単純に沿っていることに注意してください。
セクションの中では、訓練のエポック数を指定していることにも注意してください。
これは、訓練の様子を明らかにするために行っています。
実際には、早期打ち切りのテクニックが有効です。
早期打ち切りは、検証データごとに精度を調査して、精度がそれ以上向上しなくなった段階で訓練を打ち切る方法でした。
>>> import network3
>>> from network3 import Network
>>> from network3 import ConvPoolLayer, FullyConnectedLayer, SoftmaxLayer
>>> training_data, validation_data, test_data = network3.load_data_shared()
>>> mini_batch_size = 10
>>> net = Network([
FullyConnectedLayer(n_in=784, n_out=100),
SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size)
>>> net.SGD(training_data, 60, mini_batch_size, 0.1,
validation_data, test_data)
$97.80%の分類精度を得ました。 この結果は、検証データを使って、最高の分類精度を発揮する訓練エポック数を探し、 その訓練エポック数をテストデータに適用した時の精度です。 検証データを使って精度評価のタイミングを決定することで、テストデータへ過適合を防ぎます。 (検証データの使用に関する前章での議論を確認してください) このやり方を今後も踏襲します。 なお、ネットワークの重みとバイアスはランダムに初期化される*ため、あなたの結果は少し異なるかもしれません。 *私は、この実験で同じネットワークに対し3回実行しました。 検証データによる精度が3つのうちで最も良かった条件下での、テストデータによる結果を報告しました。 複数回実行することで結果のばらつきを小さくできます。 私たちが行っているように、多くの構造を比較する際にはこの方法は便利です。 以降では明記していない限り、この手続きをとっています。 実際には、この手続きを行っても、あまり結果に違いは生まれません。
この $97.80$ %という分類精度は、3章で得た $98.04$ という結果に近いです。 3章でも似たネットワーク構造を使って、ハイパーパラメータを学んでいました。 どちらの例も、$100$ 個のニューロンからなる隠れ層を1つ持つ浅いネットワークを使っています。 さらにどちらも、訓練エポック数 $60$、ミニバッチサイズ $10$、学習率 $\eta = 0.1$ の条件で訓練を行っています。
しかしネットワーク前方において、異なる点が2つあります。 1つ目は、3章のネットワークでは、前方において正規化を行っていたことです。 これにより過適合を防いでいました。 一方、この章のネットワークに対して同様に正規化を施すと、精度は向上しますが、その上がり幅はわずかです。 そのため、私たちは正規化に関しては終盤まで気にしないこととします。 2つ目は、ネットワーク前方の最後の層は、活性化関数としてシグモイドと、誤差関数として交差エントロピー関数を用いていたのに対して、現在のネットワークは活性化関数としてソフトマックス関数を、誤差関数として対数尤度関数を使っている点です。 3章で説明したように、これは大きな差異ではありません。 特に深い理由なくこのようにしています。 実際の理由は、ソフトマックス関数と対数尤度誤差を同時に使うのが、画像分類のネットワークでは常套手段だからです。
もっと深いネットワークを使えば、より良い結果を得られるでしょうか?
さぁ、ネットワークの最初の層へ、畳み込み層を挿入するところから始めましょう。 $5 \times 5$ の局所受容野、$1$ のストライド長さ、$20$ 個の特徴マップを使います。 さらにMaxプーリング層を挿入します。 このプーリング層は $2 \times 2$ のプーリングウィンドウを用いて特徴を結合します。 したがって、ネットワーク構造全体は、追加の全結合層以外は上のセクションで議論したものに近いです。
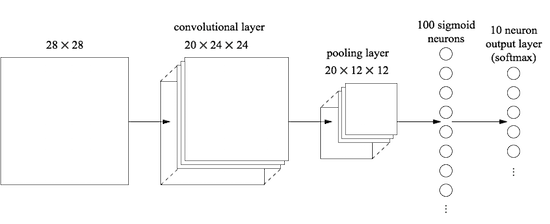
この構造の場合、畳込み層とプーリング層が入力の訓練画像内の局所空間構造を学び、 後方の層で全結合層が、もう少し抽象的なレベルで画像全体の統合情報を学ぶとみなせます。 これは畳み込みニューラルネットワークの典型的なパターンです。
そのようなネットワークを訓練してみて、どう振る舞うか見てみましょう*。 *$10$ のサイズのミニバッチをここでも使い続けています。 実際は、以前議論したように、ミニバッチのサイズを大きくすれば訓練は高速化できるでしょう。 同じミニバッチサイズを使っているのは、以前の章で行った実験と一貫性を保つためです。
>>> net = Network([
ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28),
filter_shape=(20, 1, 5, 5),
poolsize=(2, 2)),
FullyConnectedLayer(n_in=20*12*12, n_out=100),
SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size)
>>> net.SGD(training_data, 60, mini_batch_size, 0.1,
validation_data, test_data)
今回の分類精度は $98.78$ となり、これまでで最高の結果でした。 実際、誤差率を3分の1以上減らしました。 これは素晴らしい改良です。
ネットワーク構造を確認すると、畳み込み層とプーリング層をまとめて1つの層と扱っています。 別々の層としてみなすか、1つの層とみなすかは好みの問題です。 network3.pyではまとめて1つの層とみなしています。 なぜかというと、network3.pyのコードを少しコンパクトにできるからです。 しかし、お望みであれば、各層を別々に扱うようnetwork3.pyを修正することも簡単にできます。
練習問題
- 全結合層を除外して、畳み込み-プーリング層とソフトマックス層のみ使うと、分類の精度はどうなるでしょうか? 全結合層の存在が寄与しているのでしょうか?
$98.78$ % の分類精度をさらに向上できるでしょうか?
2つ目の畳み込み-プーリング層を挿入してみましょう。 既存の畳み込み-プーリング層と全結合層の間に入れます。 今回の畳み込み-プーリング層にも、$5 \times 5$ の局所受容野と $2 \times 2$ のプーリング領域という設定を適用します。 訓練時のハイパーパラメータは以前と同じ条件として、何が起きるか見てみましょう。
>>> net = Network([
ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28),
filter_shape=(20, 1, 5, 5),
poolsize=(2, 2)),
ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12),
filter_shape=(40, 20, 5, 5),
poolsize=(2, 2)),
FullyConnectedLayer(n_in=40*4*4, n_out=100),
SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size)
>>> net.SGD(training_data, 60, mini_batch_size, 0.1,
validation_data, test_data)
前回よりも良い結果です! $99.06$ %の分類精度に到達しました!
ここで2つの疑問が湧きます。 1つ目の疑問は、2層目の畳込み-プーリング層を適用した意味とは何なのか?というものです。 2層目の畳み込み-プーリング層の入力は、 $12 \times 12$ の入力"画像"とみなせます。 その各"ピクセル"は、もとの入力画像がある局所的な特徴を保持するか否かを示します。 したがって、この層はもとの入力画像の別バージョンの"画像"を入力として持つと考えられます。 そのバージョンの画像は抽象化されており情報が縮約されていますが、空間的構造は保持しています。 したがって、2層目の畳み込み-プーリング層には存在意義があると言えるのです。
これは魅力的な見方です。 でも、そうなると2つ目の疑問が湧きます。 1層目の出力は $20$ の個別の特徴マップです。 したがって、2層目の畳み込み-プーリング層への入力は $20 \times 12 \times 12$ となります。 これは、1層目の畳み込み-プーリング層の場合のように1つの画像が入力されるというよりも、 まるで $20$ の異なる入力画像が畳み込み-プーリング層に入力されるかのようです。 2層目の畳み込み-プーリング層のニューロンは、これらの多数の入力画像にどのような反応を見せるのでしょうか? 実際、2層目の自身の局所受容野中の入力ニューロン $20 \times 5 \times 5$ の全てから、2層目の各ニューロンは学習します。 ざっくり言い換えると、2層目の畳込み-プーリング層の特徴検出器は前層の特徴全てにアクセスします。 ただし、特定の局所受容野*の範囲においてのみですが。 入力がカラー画像の場合、1層目のこの問題は発生するでしょう。 その場合、入力画像の赤・緑・青のチャネルに対応する3つの特徴を各ピクセルが保持します。 したがって特徴検出器は、局所受容野の範囲内においては全ての色情報にアクセスできるのです。
問題
- 活性化関数としてtanhの使用 本書の前半の章でtanh関数はシグモイド関数よりも良い活性化関数であると述べました。 これまでは主にシグモイド関数を使って議論を進めてきましたが、tanhを活性化関数として用いて少し実験をしてみましょう。 畳み込み層と全結合層でtanhを試しに使い、ネットワークを訓練してみてください* *activation_fn=tanhをパラメータとしてConvPoolLayerとFullyConnectedLayerのクラスへ渡せます。。 シグモイドのネットワークの時と同じパラメータで始めてみましょう。 ただし、 エポック数は $60$ ではなく $20$ にします。 ネットワークはどのように振る舞うでしょうか? $60$ エポックまで続けたらどうなるでしょう? tanhの場合とシグモイドの場合で、検証データに対する精度を $60$ エポックまでプロットしてみてください。 あなたの結果が私の結果と近ければ、tanhのネットワークの方が少し高速ですが、最終的な精度はほぼ同じになったはずです。 なぜtanhのネットワークの方が高速なのか説明できますか? 学習率やスケール*などを変更することで、シグモイドと同じ速度で学習させることができるでしょうか? *$\sigma(z) = (1+\tanh(z/2))/2$ の式を思い出すことで、何かを思いつくでしょうか? tanhがシグモイドよりも優れている点を探すために、ハイパーパラメータやネットワーク構造を変更するなど、試行錯誤してください。 これは自由回答の問題であることに注意してください。 すべての設定を網羅して試せていませんが、個人的には、tanhへ活性化関数を変更する利点はないように思います。 もしかしたら利点を見つけられるかもしれません。 どちらにせよ、活性化関数をReLUへ変更する利点がこの後、見つかってしまいます。 ですので、これ以上tanhを使用することは考えません。
ReLUの使用: これまで開発してきたネットワークは、1998年の先駆的な論文*で使われたネットワークの亜種です。 *その論文とは1998年のYann LeCun, Léon Bottou, Yoshua Bengio, Patrick Haffnerによる"Gradient-based learning applied to document recognition"です。 細かいところに違いはたくさんあるのですが、ネットワーク全体で見ると私たちのネットワークに非常に似ています。 この論文では、MNISTの問題とLeNet-5というネットワークが紹介されています。 私たちの理解と直感を促進する上で、この論文は有用です。 特に、結果を良くするために何をすればよいかを示す、ネットワークの改善指針がたくさん載っています。
まず始めに、活性化関数をシグモイドではなく、ReLUに変更しましょう。 すなわち $f(z) \equiv \max(0, z)$ という活性化関数を使うようにします。 訓練のエポック数 $60$ 、学習率 $\eta = 0.03$ で訓練します。 パラメータ $\lambda = 0.1$ としてL2 正規化を使うと少し良くなるということも知っています。
>>> from network3 import ReLU
>>> net = Network([
ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28),
filter_shape=(20, 1, 5, 5),
poolsize=(2, 2),
activation_fn=ReLU),
ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12),
filter_shape=(40, 20, 5, 5),
poolsize=(2, 2),
activation_fn=ReLU),
FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU),
SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size)
>>> net.SGD(training_data, 60, mini_batch_size, 0.03,
validation_data, test_data, lmbda=0.1)
今回、 $99.23$ %の分類精度を得ました。 シグモイドの場合( $99.06$ % )と比べてほんの少し改善されました。 しかし、同一の問題に対し様々な条件で試した結果、私が発見したのは、ReLUを使うとシグモイドを使ったネットワークよりも、一貫して高精度となることです。 この問題に関しては、ReLUへ移行するのが得策のようです。
ReLUの活性化関数はシグモイドやtanh関数より何が優れているのでしょう? この問いに対する答えを今はまだ持ち合わせていません。 実際のところ、ReLUはここ数年で使われ始めたのです。 その採用の理由は、試しに使ってみた実験の結果が良かったことにあります。 最初の何人かが直感やヒューリスティックな議論*に従い、ReLUを試してみたのです。 *理由付けとしてよくあるのが、 $\max(0, z)$ は大きな $z$ に対しても飽和しないので良い、というものです。 シグモイドは飽和するのに対して、このReLUは飽和しないために学習し続けられるというのです。 この主張は直感的には合っている気がします。 しかし詳細な証明ではありません。 この飽和の問題に関する議論は2章で既に触れました。 ReLUはベンチマークのデータセットを上手く分類しました。 その実例は、さらに広がりつつあります。 理想としては、応用方法に応じて使用する活性化関数を選ぶための理論が欲しいと思います。 でも現実にそんな理論はありません。 もし仮に活性化関数をさらに上手く選ぶことができれば、結果が良くなるでしょう。 なので数十年後には、活性化関数に関する強力な理論が生まれていることを期待しています。 でも今は、大ざっぱな理論にすがり、地道な実験を繰り返して、活性化関数を選ぶしかないのです。
訓練データの拡張: 結果を改良する別の手法として、訓練データをアルゴリズムを使って拡張する手法があります。 シンプルなやり方は、訓練データの各画像を1ピクセルずつ上下左右のいずれかの方向にずらすことです。 expand_mnist.pyのプログラムをシェルプロンプトから動かして試せます*。 *expand_mnist.pyのコードはここで取得できます。
$ python expand_mnist.py
このプログラムを実行すると、入力の $50,000$ のMNISTの訓練画像を、 $250,000$ と増やします。 新たに生成した画像もネットワークを訓練するのに使えます。 今回も上のネットワークと同じようにReLUを使います。 最初の実験では、訓練のエポック数を減らしました。 しかし、訓練データを増やすことで、過適合を防ぐ効果が期待できます。 そのため幾つかの実験を経た後で、私はエポック数を $60$ へ戻しました。 さあ、訓練してみましょう。
>>> expanded_training_data, _, _ = network3.load_data_shared(
"../data/mnist_expanded.pkl.gz")
>>> net = Network([
ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28),
filter_shape=(20, 1, 5, 5),
poolsize=(2, 2),
activation_fn=ReLU),
ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12),
filter_shape=(40, 20, 5, 5),
poolsize=(2, 2),
activation_fn=ReLU),
FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU),
SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size)
>>> net.SGD(expanded_training_data, 60, mini_batch_size, 0.03,
validation_data, test_data, lmbda=0.1)
拡張した訓練データを使った結果、 $99.37$ %の分類精度を得ました。 データに僅かな変化を施したことで、精度が向上したのです。 データ拡張により結果が良くなることは以前にも議論しました。 この時の議論の雰囲気を思い出してもらいましょう。 2003年にSimard, Steinkraus, Platt*はMNISTに対する分類精度を $99.6$ まで向上しました。 その時には、2つの畳み込み-プーリング層とそれに続く $100$ のニューロンを持つ全結合層からなるネットワークを使っていました。 これは私たちのネットワークに非常に近いです。 *2003年のPatrice Simard, Dave Steinkraus, John Plattによる Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis。 しかし、私たちのネットワークと彼らのネットワークの構造には細かい違いが幾つかあります。 例えば、ReLUを使っていなかったことなどです。 しかし、パフォーマンスが非常に良かった大きな理由は訓練データの拡張にあります。 彼らはMNISTの訓練画像に対して、回転・並進移動・せん断の操作を行いました。 さらに"elastic distortion"の操作も加えました。 これは、人が数字を書く時に手の筋肉がランダムに振動する様子を模擬する方法です。 これらの操作を組み合わせて、訓練データを実質的に増やし、 $99.6$ %の分類精度を達成しました。
問題
- 畳み込み層のアイデアとは、画像に対して並進方向の不変性を持つことです。 となると、入力画像に対して並進移動の操作を加えて訓練データを増やしたときに、ネットワークの精度が向上するのは一見不思議です。 なぜこれがとても合理的なのか説明できますか?
全結合層の追加: さらに改良できるでしょうか? 1つの可能性としては、上記と同じ手続きを行いながらも、サイズの大きな全結合層を追加してみることです。 $300$ と $1,000$ のニューロンを持つ全結合層を追加して、それぞれ試したところ、それぞれ $99.46$ %と $99.43$ %の結果を得ました。 これは興味深いですが、前回の結果($99.37$ %)とあまり変わりませんでした。
さらに全結合層を追加してみたらどうでしょうか? さあ、全結合層を1層追加して、$100$ ニューロンからなる全結合層を2つ持つネットワークとしましょう。
>>> net = Network([
ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28),
filter_shape=(20, 1, 5, 5),
poolsize=(2, 2),
activation_fn=ReLU),
ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12),
filter_shape=(40, 20, 5, 5),
poolsize=(2, 2),
activation_fn=ReLU),
FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU),
FullyConnectedLayer(n_in=100, n_out=100, activation_fn=ReLU),
SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size)
>>> net.SGD(expanded_training_data, 60, mini_batch_size, 0.03,
validation_data, test_data, lmbda=0.1)
これにより、$99.43$ の分類精度を得ました。 全結合層を追加しただけでは、またしても、精度が向上しませんでした。 ニューロン数を $300$ と $1,000$ とした全結合層の場合でも同じ実験をしてみましたが、それぞれ $99.48$ %と $99.47$ %という結果でした。 悪くないですが、格段には向上していません。
何が起きているのでしょうか? 全結合層を増やすのは、MNIST問題には有効でないのでしょうか? もしくはネットワークは改良されているのに、私たちが間違ったやり方で訓練しているのでしょうか? 例えば、過適合を回避するために、より強力な正規化のテクニックを使うのもよいでしょう。 別の例としては、3章で紹介したドロップアウトのテクニックがあります。 ドロップアウトの基礎的なアイデアを思い出してください。 訓練時に各活性化出力をランダムに0とするのです。 これによりモデルが、各入力の有無の違いにロバストになるため、各訓練データの特異性に依存しなくなります。 このドロップアウトを最後の全結合層に適用してみましょう。
>>> net = Network([
ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28),
filter_shape=(20, 1, 5, 5),
poolsize=(2, 2),
activation_fn=ReLU),
ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12),
filter_shape=(40, 20, 5, 5),
poolsize=(2, 2),
activation_fn=ReLU),
FullyConnectedLayer(
n_in=40*4*4, n_out=1000, activation_fn=ReLU, p_dropout=0.5),
FullyConnectedLayer(
n_in=1000, n_out=1000, activation_fn=ReLU, p_dropout=0.5),
SoftmaxLayer(n_in=1000, n_out=10, p_dropout=0.5)],
mini_batch_size)
>>> net.SGD(expanded_training_data, 40, mini_batch_size, 0.03,
validation_data, test_data)
これにより $99.60$ %の分類精度を得ました。 やっと $100$ のニューロンからなるネットワークのベンチマーク結果である $99.37$ を大きく更新しました。
2つの注目すべき変化があります。
1つ目は、訓練するエポック数を $40$ に減らしたことです。 ドロップアウトが過適合を抑制するため、高速に学習できるのです。
2つ目は、全結合層内のニューロン数が以前と同じ $100$ 個ではなく、 $1,000$ 個であることです。 ドロップアウトはニューロンの多くを効率的に省いているので、ニューロン数の増量が必要なのです。 実際、$300$ と $1,000$ の隠れニューロンを使って実験もしてみましたが、$1,000$ ニューロンの場合の方が(僅かですが)結果が良かったです。
ネットワークのアンサンブルの活用: パフォーマンスをさらに向上させる簡単な方法は、複数のニューラルネットワークを作成し、それらに多数決で分類を決めさせることです。 例えば、上述の条件を満たす $5$ つの異なるニューラルネットワークを訓練して、それぞれ $99.6$ %の精度を得たと想定します。 各ネットワークは精度は同等だったとしても、ランダムな初期化がされているため誤差の出し方が異なります。 つまり、これら $5$ つのニューラルネットワーク間で多数決を取れば、個々のニューラルネットワークだけの場合よりも良い分類が可能となるはずです。
あまりに上手く行きそうなので、胡散臭いですね。 でも、この種のアンサンブル手法はニューラルネットワークや他の機械学習での常套手段です。 そして実際、精度は向上し、 $99.67$ %となりました。 この結果を言い換えると、ネットワークのアンサンブルにより $10,000$ のテスト画像のうち、$33$ 以外の全てを正しく分類できたのです。
テストセットで間違えたものを下に示します。 右上のラベルはMNISTによる正しい分類を示し、右下はネットワークのアンサンブルによる出力を示します。

この結果は細かく確認する価値があります。 最初の2つの数字、"6"と"5"はアンサンブルが判断した間違いです。 しかし、それらはいずれも理解できる間違いです。 人間でも間違えそうです。 その"6"は"0"のように見えますし、"5"は"3"のように見えます。 3つめの画像は"8"のはずですが、実際には"9"に近く見えます。 なので、私はネットワークのアンサンブルの判断の方が正しいように思えます。 つまり、その数字を書いた人よりもネットワークのほうが良い仕事をしていると思います。 一方、4つ目の画像の"6"はネットワークによる分類は不思議に感じます。
大抵のケースでは私たちのネットワークの選択は、少なくとももっともらしいように見えます。 幾つかのケースでは、数字を書いた人よりも良いはたらきをしています。 上記に示さなかった9,967の画像を考慮すると、全体として私たちのネットワークは素晴らしいパフォーマンスを発揮していると言えます。 そのような文脈を考えると、僅かにある分類の明らかな誤りも許容できます。 現実にはどんなに注意深い人間でさえも、時には間違いを犯します。 したがって、とんでもなく注意深くて理論的な人間だけがこのネットワークよりもよい精度を出せると思います。 私たちのネットワークは人間の最高精度に到達しつつあるのです。
なぜ全結合層だけにドロップアウトを適用したのか: 上記のコードを注意深く見ると、ドロップアウトを全結合層にのみ適用しており、 畳み込み層へは適用していないことに気づくでしょう。 原理的には、畳み込み層に対しても同じ手続きを適用できます。 しかし、実際その必要はありません。 畳み込み層は過適合に対するもともとの抵抗力が強いのです。 その理由は、重みを共有することにより、畳込みフィルタが画像全体から学習することなるからです。 これにより訓練データの局所的な特異性による影響を受けにくくなっています。 したがって、ドロップアウトなどの他の正規化手法を適用する必要性が薄いのです。
さらなる性能向上をめざして: MNIST問題に対する性能をもっと上げることはできます。 Rodrigo Benensonが 有益なまとめページを作っています。 このページでは年々の進化を、論文にリンクした形で確認できます。 これらの論文では、私たちが使ってきたものと、近しい深層畳み込みネットワークを使用しています。 論文を漁れば、面白いテクニックがたくさん見つかるでしょう。 それを実装するのは楽しいはずです。 もし実装する場合には、高速に訓練ができる単純なネットワークを使うのが賢いと思います。 そういったネットワークでは、何が起きているのかをすぐに理解しやすいからです。
私は最近の大抵の論文を調査しようとしません。 しかし、1つだけ例外があります。 2010年のCireșan, Meier, Gambardella, Schmidhuberによる論文です* *2010年のDan Claudiu Cireșan, Ueli Meier, Luca Maria Gambardella, Jürgen SchmidhuberによるDeep, Big, Simple Neural Nets Excel on Handwritten Digit Recognition。。 この論文はシンプルさが好きです。 ネットワークは多層で、全結合層のみを使っています(畳み込み層はなし)。 最も成功したネットワークは $2500$, $2000$, $1500$, $1000$, $500$ のニューロンをそれぞれ含む全結合層からなるネットワークです。 訓練データを拡張するためにSimard et alに似たアイデアを使っています。 しかし、それ以外にも幾つかのトリックを用いています。 その1つは畳み込み層を使わないことです。 簡素で平凡ですが、1980年代(もしMNISTデータセットがあったとしたら)であっても計算機の能力さえあれば同じことが可能です。 彼らは私たちと同等程度の $99.65$ %の分類精度を達成しました。 ポイントはとても深いネットワークを使い、GPUで高速に訓練したことです。 エポック数を大きく取って訓練しています。 訓練時間を長く取ることで、学習率を $10^{-3}$ から $10^{-6}$ へ徐々に減少させています。 論文のネットワーク構造を使って、結果が合うかどうか試してみるのは楽しい演習になるでしょう。
なぜ訓練できるのでしょうか? 前章で、深くて多層のニューラルネットワークの訓練における本質的な障壁について 学びました。 特に、勾配がとても不安定になる問題を確認しました。 出力層から前方の層に遡るにしたがって、勾配は消失(勾配消失問題)するか、爆発(勾配爆発問題)してしまう傾向があります。 勾配は訓練のきっかけとなるものなので、勾配が不安定になると問題となります。
では、どうやってこの問題を避けているのでしょうか?
もちろん答えは、この問題を回避していない、というものです。 代わりに、結果を良くするための操作を幾つか行っています。 (1)畳み込み層を使うことで、層のパラメータ数が劇的に減っているため、学習に伴う問題が起きにくくなっています。 (2)強力な正規化テクニック(特にドロップアウトと畳込み層)を使うことで、他の複雑なネットワークでは問題となる過適合を防いています。 (3)シグモイドの代わりにReLUを使うことで、訓練を高速に行っています。 実験では $3$-$5$ 倍速くなっています。 (4) GPUを使って訓練時間を長くしています。特に、最後の実験では、もとのMNISTの訓練データの $5$ 倍のデータを用いて $40$ エポック分訓練しています。 本書の前半ではもとの訓練データを用いて、 $30$ エポック分訓練していました。 (3) と (4) の要素を組み合わせると以前の $30$ 倍長く時間がかかります。
あなたはきっと、 「それだけ?深いネットワークの訓練に必要な工夫は本当にそれだけ?(これまでさんざん苦労してきたのに)一体どうなってるの?」と思うでしょう。
もちろん、他の工夫も加えています。 過適合を防ぐために十分大きなデータセットを利用したり、 学習が遅くなるのを防ぐために正しいコスト関数を使ったり、 ニューロンの飽和による学習の遅延を防ぐために重みを上手く初期化したり、 訓練データをアルゴリズムで拡張したりしました。 上記の工夫についてはこれまでの章で解説してきたので、この章では説明が少なくても理解できるでしょう。
これらの工夫はシンプルなものです。 シンプルですが、同時に使用すると強力です。 ディープラーニングがとても容易になります!
ところで、これらのネットワークの深さはどのくらい? 畳み込み-プーリング層を1つの層として数えると、私たちの最後のネットワークは隠れ層を $4$ つ持つこととなります。 このネットワークは本当に 深層ネットワークと呼ばれるに値するのでしょうか? もちろん、これまで学んできた他の浅いネットワークと比べると $4$ つの隠れ層というのは深いです。 これまでの浅いネットワークは $1$ つ、もしくは $2$ つだけ隠れ層を持っていました。 一方、2015年の最新の深層ネットワークは $10$ 以上の隠れ層を持ちます。 最近はとにかく層を深くする傾向があります。 聞くところによると、隠れ層の数で周囲に遅れを取っているのでは、ディープラーニングと呼べないというのです。 しかし、一時的な結果に依存する何かをディープラーニングと呼ぶことになってしまうため、私はこの態度には共感しません。 ディープラーニングの本当のブレークスルーは、2000年代中盤まで支配的だった浅い $1$ 層や $2$ 層のネットワーク以外でも実用的な結果が得られることが判明したことだと思っています。 それは、はるかに表現力豊かなモデルを探索する機会を得るという意味で真のブレークスルーでした。 しかしそれを除いても、層の深さは本質的な議論ではありません。 むしろ、他の目的に深いネットワークをいかに応用できるかの方が重要です。
注意点: このセクションでは、単一の隠れ層を持つ浅いネットワークから多層の畳み込みネットワークへ順調に移行しました。 畳み込みネットワークは簡単そうです! ネットワークに変更を加えることで、すぐに結果が良くなりました。 しかしあなたが実験を始めても、その直後は上手く行くとは限らないことを私は保証します。 その理由は、実際には多くの実験を行っているにも関わらず、本書ではそれらを省略した無駄のない文脈で、畳み込みネットワークを紹介したからです。 失敗に終わった実験を裏でたくさん行っています。 無駄のない文脈で説明してきたので、あなたの基礎理解は深まったと思っています。 しかし、誤解を与えた恐れもありますね。 上手く行くネットワークに辿り着くには、イライラしながら試行錯誤をする必要があります。 実際、多くの実験をこなさなければならないはずです。 その時には、3章の ニューラルネットワークのハイパーパラメータをどう選ぶかの議論が作業効率化の助けになります。 そして、この章の残りを読むことも重要です。
畳み込みネットワークのコード
さあ、私たちのコードnetwork3.pyを見てみましょう。 3章で開発したnetwork2.pyに構造的に似ています。 ただし、Theanoを導入したため、詳細は異なっています。 まずFullyConnectedLayerのクラスから確認を始めましょう。 これは本書で既に扱ってきた層に似ています。 コードはこのようになっています* self.wを初期化する行で、scale=np.sqrt(1.0/n_out)としているのに気づいた人もいるでしょう。 3章の議論ではscale=np.sqrt(1.0/n_in)を使うように推していたのに、何故この方法を取っているのかと不思議に感じる方もいると思います。 実を言うと、これは単純に私のミスです。 本当は、この章のコードを修正しなくてはいけないのですが、現在私は他のプロジェクトにかかりきりになっているので、しばらくはそのままにしておきます。 。
class FullyConnectedLayer(object):
def __init__(self, n_in, n_out, activation_fn=sigmoid, p_dropout=0.0):
self.n_in = n_in
self.n_out = n_out
self.activation_fn = activation_fn
self.p_dropout = p_dropout
# Initialize weights and biases
self.w = theano.shared(
np.asarray(
np.random.normal(
loc=0.0, scale=np.sqrt(1.0/n_out), size=(n_in, n_out)),
dtype=theano.config.floatX),
name='w', borrow=True)
self.b = theano.shared(
np.asarray(np.random.normal(loc=0.0, scale=1.0, size=(n_out,)),
dtype=theano.config.floatX),
name='b', borrow=True)
self.params = [self.w, self.b]
def set_inpt(self, inpt, inpt_dropout, mini_batch_size):
self.inpt = inpt.reshape((mini_batch_size, self.n_in))
self.output = self.activation_fn(
(1-self.p_dropout)*T.dot(self.inpt, self.w) + self.b)
self.y_out = T.argmax(self.output, axis=1)
self.inpt_dropout = dropout_layer(
inpt_dropout.reshape((mini_batch_size, self.n_in)), self.p_dropout)
self.output_dropout = self.activation_fn(
T.dot(self.inpt_dropout, self.w) + self.b)
def accuracy(self, y):
"Return the accuracy for the mini-batch."
return T.mean(T.eq(y, self.y_out))
__init__の大部分は自明ですが、少し解説しておくとコードの意味が明快になるでしょう。 通常通り、適切な標準偏差を設定して重みとバイアスをランダムにばらつかせて初期化しています。 この操作を行っている行は少し馴染みが薄いかもしれません。 でも、複雑そうに見える処理は実は、重みとバイアスをTheanoが共有変数と呼ぶ変数へ渡しているだけです。 この操作は、GPU実行可能であれば、この変数がGPU上で処理されることを保証するというものです。 詳細にはこれ以上踏み込みません。 興味があれば、Theanoのドキュメントを参照してください。 この重みとバイアスの初期化は、以前議論したようにシグモイドの活性化関数を考慮して行われていることにも注意してください。 理想的には、重みとバイアスの初期化をtanhやReLU向けに、少し異なる方法で行うのがよいでしょう。 これは後々議論します。 __init__関数はself.params = [self.w, self.b]を行い終了します。 この処理は、層に関連する学習可能なパラメータをまとめる手軽な方法です。 後々、Network.SGD関数がparamsの属性を使うときに、 Networkのインスタンスが学習するパラメータを明らかにしているのです。
set_inpt関数は層への入力を設定し、対応する出力を計算するために使われます。 inputではなくinptという名前を使っているのは、Pythonにinputというビルトイン関数があるためです。 ビルトイン関数と混在すると、予測不能な振る舞いが起きる恐れがあったので避けました。 さて、入力を2つの異なる方法で設定していることに注意してください。 それぞれself.inptとself.inpt_dropoutです。 訓練時にはドロップアウトを使いたいと思うかもしれないので、こうしました。 その時には、self.p_dropoutのニューロンの一部を取り除く必要があります。 それが、関数dropout_layerの最後から2行目のset_inpt関数が行っていることです。 したがって、self.inpt_dropoutとself.output_dropoutは訓練時に使用されます。 一方、self.inptとself.outputは、例えば、検証データとテストデータの精度を評価する場合など、どのような場合にも使われます。
ConvPoolLayerとSoftmaxLayerクラスの定義はFullyConnectedLayerの定義と似ています。 本当にそっくりなので、ここではコードを引用しません。 興味があれば、このセクションの後にあるnetwork3.pyの全コードを参照してください。
しかし、いくつかの細かい違いに着目するのは悪くありません。 ConvPoolLayerとSoftmaxLayerは、 層の種類に応じて適切な出力の活性化を行っています。 幸運なことに、Theanoの提供するビルトイン演算操作を使えば、畳み込みやMaxプーリング、ソフトマックス関数の計算を簡単に行なえます。
さらに、些細な事ですが、 ソフトマックス層を導入した際、重みとバイアスの初期化の仕方を議論しませんでした。 一方、シグモイドの層では、重みを適切なランダム値に初期化するべきであることは既に述べました。 しかし、そのヒューリスティックな議論はシグモイドニューロン(と少し修正を加えればtanh)に特有なものです。 同じ議論をソフトマックス層に適用すべき理由は特にありません。 したがって、その初期化法を適用するア・プリオリな理由はないのです。 むしろ、$0$ で全ての重みとバイアスを初期化した方がよいと思います。 これはとても場当たり的なやり方に見えますが、実践では十分上手くいきます。
よし、これで層の全種類のクラス定義を確認したことになります。 Networkクラスはどうでしょう? __init__関数を見るところから始めましょう。
class Network(object):
def __init__(self, layers, mini_batch_size):
"""Takes a list of `layers`, describing the network architecture, and
a value for the `mini_batch_size` to be used during training
by stochastic gradient descent.
"""
self.layers = layers
self.mini_batch_size = mini_batch_size
self.params = [param for layer in self.layers for param in layer.params]
self.x = T.matrix("x")
self.y = T.ivector("y")
init_layer = self.layers[0]
init_layer.set_inpt(self.x, self.x, self.mini_batch_size)
for j in xrange(1, len(self.layers)):
prev_layer, layer = self.layers[j-1], self.layers[j]
layer.set_inpt(
prev_layer.output, prev_layer.output_dropout, self.mini_batch_size)
self.output = self.layers[-1].output
self.output_dropout = self.layers[-1].output_dropout
コードの大部分は見ればわかると思います。 self.params = [param for layer in ...]の行では、各層のパラメータを1つのリストにまとめています。 上で触れたように、Network.SGD関数がself.paramsを観て、Networkの中のどの変数が学習するのかを把握します。 self.x = T.matrix("x")とself.y = T.ivector("y")の行は、xとyと名付けたTheanoのシンボリック変数を定義する部分に当たります。 これらの変数は、入力とネットワークの望みの出力を表現するのに使われます。
さて本書はTheanoのチュートリアルではないので、シンボリック変数*の意味については深く踏み込みません *Theanoの導入にはTheanoのドキュメントを読むべきです。 もし詰まったら、オンラインにある他のチュートリアルを参照すると良いでしょう。 例えば、このチュートリアルは基礎を広く押さえています。。 しかし簡単に説明しておくと、シンボリック変数とは数学的な変数であり、値を表すものではありません。 加算、減算、乗算や関数の適用などの操作をシンボリック変数へ施すことができます。 他にも、畳み込みやMaxプーリングなどの、シンボリック変数を操作する方法をTheanoは多数提供しています。 シンボリック変数を使う大きな利点は、逆伝播のアルゴリズムで必要な微分を高速なシンボリック微分として行える点です。 確率的勾配降下法を様々なネットワーク構造に対して実行するにあたって、これはとても強力に感じます。 次の数行では、ネットワークの出力を定義しています。 その際、最初の層へ入力を設定するところから始まっています。
init_layer.set_inpt(self.x, self.x, self.mini_batch_size)
入力が1つのミニバッチに一度に設定されることに注意してください。 入力self.xを2つの引数として渡していることにも注意してください。 これは、ネットワークを(ドロップアウトの有無で)2つの異なる方法で使うためです。 forループでは、Networkの層間をシンボリック変数self.xが順伝播していきます。 これにより、最後のoutputとoutput_dropoutの中身を定義することができます。 これらはNetworkの出力を表現します。
これで、Networkがどのように初期化されるかがわかりました。 さあSGD関数による訓練方法を見ていきましょう。 コードは長いですが、構造は実にシンプルです。 コードの後に説明のコメントを記します。
def SGD(self, training_data, epochs, mini_batch_size, eta,
validation_data, test_data, lmbda=0.0):
"""Train the network using mini-batch stochastic gradient descent."""
training_x, training_y = training_data
validation_x, validation_y = validation_data
test_x, test_y = test_data
# compute number of minibatches for training, validation and testing
num_training_batches = size(training_data)/mini_batch_size
num_validation_batches = size(validation_data)/mini_batch_size
num_test_batches = size(test_data)/mini_batch_size
# define the (regularized) cost function, symbolic gradients, and updates
l2_norm_squared = sum([(layer.w**2).sum() for layer in self.layers])
cost = self.layers[-1].cost(self)+\
0.5*lmbda*l2_norm_squared/num_training_batches
grads = T.grad(cost, self.params)
updates = [(param, param-eta*grad)
for param, grad in zip(self.params, grads)]
# define functions to train a mini-batch, and to compute the
# accuracy in validation and test mini-batches.
i = T.lscalar() # mini-batch index
train_mb = theano.function(
[i], cost, updates=updates,
givens={
self.x:
training_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
self.y:
training_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
validate_mb_accuracy = theano.function(
[i], self.layers[-1].accuracy(self.y),
givens={
self.x:
validation_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
self.y:
validation_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
test_mb_accuracy = theano.function(
[i], self.layers[-1].accuracy(self.y),
givens={
self.x:
test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
self.y:
test_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
self.test_mb_predictions = theano.function(
[i], self.layers[-1].y_out,
givens={
self.x:
test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
# Do the actual training
best_validation_accuracy = 0.0
for epoch in xrange(epochs):
for minibatch_index in xrange(num_training_batches):
iteration = num_training_batches*epoch+minibatch_index
if iteration
print("Training mini-batch number {0}".format(iteration))
cost_ij = train_mb(minibatch_index)
if (iteration+1)
validation_accuracy = np.mean(
[validate_mb_accuracy(j) for j in xrange(num_validation_batches)])
print("Epoch {0}: validation accuracy {1:.2
epoch, validation_accuracy))
if validation_accuracy >= best_validation_accuracy:
print("This is the best validation accuracy to date.")
best_validation_accuracy = validation_accuracy
best_iteration = iteration
if test_data:
test_accuracy = np.mean(
[test_mb_accuracy(j) for j in xrange(num_test_batches)])
print('The corresponding test accuracy is {0:.2
test_accuracy))
print("Finished training network.")
print("Best validation accuracy of {0:.2
best_validation_accuracy, best_iteration))
print("Corresponding test accuracy of {0:.2
最初の数行は単純です。 データセットを $x$ と $y$ の要素に分けて、各データセットで使われるミニバッチの数を計算しています。 次の数行は興味深く、Theanoの醍醐味となる部分です。 その行をここに引用してみましょう。
# define the (regularized) cost function, symbolic gradients, and updates
l2_norm_squared = sum([(layer.w**2).sum() for layer in self.layers])
cost = self.layers[-1].cost(self)+\
0.5*lmbda*l2_norm_squared/num_training_batches
grads = T.grad(cost, self.params)
updates = [(param, param-eta*grad)
for param, grad in zip(self.params, grads)]
これらの行では、正規化した対数尤度の誤差関数を用意しています。 また、パラメータの更新に応じて、勾配関数の中の対応する微分を計算します。 Theanoを使うと数行でこれら全てを実装できます。 隠されていて唯一分かりにくいのは、costの計算の時に出力層のcost関数を呼ぶことです。 このcost関数はnetwork3.py内の別の箇所にあります。 しかし、そのコードは短くシンプルです。 さて、これら全ての設定が終わると、train_mb関数を定義する段階へ移ります。 このTheanoのシンボリック関数はupdatesを用い、ミニバッチのインデックスをもとにNetworkのパラメータを更新します。 同様に、validate_mb_accuracyとtest_mb_accuracyは、検証データやテストデータのミニバッチに基づいて、Networkの精度を計算します。 これらの関数の結果の平均をとって、検証データやテストデータの全体精度を計算できるのです。
SGD関数の残りの部分は自明だと思います。 単純にエポック数分だけ反復し、訓練データのミニバッチに基づいてネットワークを訓練し、検証データとテストデータの精度を計算します。
よし、これでnetwork3.pyの重要な部分は理解したことになります。 プログラム全体を見てみましょう。 コードを詳細に読み解く必要はありません。 きっと、コードを眺めるだけで楽しいはずです。 あなたが気になった箇所を深掘りしてみるのも良いと思います。 もちろん、コードを深く理解するための一番良い方法は、コードに修正を加えたり、何か特徴を追加したり、もしくはエレガントになるようリファクタリングしてみることです。 コードの後ろに、いくつか修正すべき項目を載せています* *Theanoを使ってコードをGPU実行する方法は少しトリッキーです。 特に、GPUからデータを取得するところは間違えやすく、間違えるとかなり低速になってしまいます。 私はこれを避けようと試行錯誤してきました。 このコードではTheanoの最適化設定を注意深く行っているため、かなり高速に動作するはずです。 詳細はTheanoのドキュメントを見て確認してください。
"""network3.py
~~~~~~~~~~~~~~
A Theano-based program for training and running simple neural
networks.
Supports several layer types (fully connected, convolutional, max
pooling, softmax), and activation functions (sigmoid, tanh, and
rectified linear units, with more easily added).
When run on a CPU, this program is much faster than network.py and
network2.py. However, unlike network.py and network2.py it can also
be run on a GPU, which makes it faster still.
Because the code is based on Theano, the code is different in many
ways from network.py and network2.py. However, where possible I have
tried to maintain consistency with the earlier programs. In
particular, the API is similar to network2.py. Note that I have
focused on making the code simple, easily readable, and easily
modifiable. It is not optimized, and omits many desirable features.
This program incorporates ideas from the Theano documentation on
convolutional neural nets (notably,
http://deeplearning.net/tutorial/lenet.html ), from Misha Denil's
implementation of dropout (https://github.com/mdenil/dropout ), and
from Chris Olah (http://colah.github.io ).
Written for Theano 0.6 and 0.7, needs some changes for more recent
versions of Theano.
"""
#### Libraries
# Standard library
import cPickle
import gzip
# Third-party libraries
import numpy as np
import theano
import theano.tensor as T
from theano.tensor.nnet import conv
from theano.tensor.nnet import softmax
from theano.tensor import shared_randomstreams
from theano.tensor.signal import downsample
# Activation functions for neurons
def linear(z): return z
def ReLU(z): return T.maximum(0.0, z)
from theano.tensor.nnet import sigmoid
from theano.tensor import tanh
#### Constants
GPU = True
if GPU:
print "Trying to run under a GPU. If this is not desired, then modify "+\
"network3.py\nto set the GPU flag to False."
try: theano.config.device = 'gpu'
except: pass # it's already set
theano.config.floatX = 'float32'
else:
print "Running with a CPU. If this is not desired, then the modify "+\
"network3.py to set\nthe GPU flag to True."
#### Load the MNIST data
def load_data_shared(filename="../data/mnist.pkl.gz"):
f = gzip.open(filename, 'rb')
training_data, validation_data, test_data = cPickle.load(f)
f.close()
def shared(data):
"""Place the data into shared variables. This allows Theano to copy
the data to the GPU, if one is available.
"""
shared_x = theano.shared(
np.asarray(data[0], dtype=theano.config.floatX), borrow=True)
shared_y = theano.shared(
np.asarray(data[1], dtype=theano.config.floatX), borrow=True)
return shared_x, T.cast(shared_y, "int32")
return [shared(training_data), shared(validation_data), shared(test_data)]
#### Main class used to construct and train networks
class Network(object):
def __init__(self, layers, mini_batch_size):
"""Takes a list of `layers`, describing the network architecture, and
a value for the `mini_batch_size` to be used during training
by stochastic gradient descent.
"""
self.layers = layers
self.mini_batch_size = mini_batch_size
self.params = [param for layer in self.layers for param in layer.params]
self.x = T.matrix("x")
self.y = T.ivector("y")
init_layer = self.layers[0]
init_layer.set_inpt(self.x, self.x, self.mini_batch_size)
for j in xrange(1, len(self.layers)):
prev_layer, layer = self.layers[j-1], self.layers[j]
layer.set_inpt(
prev_layer.output, prev_layer.output_dropout, self.mini_batch_size)
self.output = self.layers[-1].output
self.output_dropout = self.layers[-1].output_dropout
def SGD(self, training_data, epochs, mini_batch_size, eta,
validation_data, test_data, lmbda=0.0):
"""Train the network using mini-batch stochastic gradient descent."""
training_x, training_y = training_data
validation_x, validation_y = validation_data
test_x, test_y = test_data
# compute number of minibatches for training, validation and testing
num_training_batches = size(training_data)/mini_batch_size
num_validation_batches = size(validation_data)/mini_batch_size
num_test_batches = size(test_data)/mini_batch_size
# define the (regularized) cost function, symbolic gradients, and updates
l2_norm_squared = sum([(layer.w**2).sum() for layer in self.layers])
cost = self.layers[-1].cost(self)+\
0.5*lmbda*l2_norm_squared/num_training_batches
grads = T.grad(cost, self.params)
updates = [(param, param-eta*grad)
for param, grad in zip(self.params, grads)]
# define functions to train a mini-batch, and to compute the
# accuracy in validation and test mini-batches.
i = T.lscalar() # mini-batch index
train_mb = theano.function(
[i], cost, updates=updates,
givens={
self.x:
training_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
self.y:
training_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
validate_mb_accuracy = theano.function(
[i], self.layers[-1].accuracy(self.y),
givens={
self.x:
validation_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
self.y:
validation_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
test_mb_accuracy = theano.function(
[i], self.layers[-1].accuracy(self.y),
givens={
self.x:
test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
self.y:
test_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
self.test_mb_predictions = theano.function(
[i], self.layers[-1].y_out,
givens={
self.x:
test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
})
# Do the actual training
best_validation_accuracy = 0.0
for epoch in xrange(epochs):
for minibatch_index in xrange(num_training_batches):
iteration = num_training_batches*epoch+minibatch_index
if iteration % 1000 == 0:
print("Training mini-batch number {0}".format(iteration))
cost_ij = train_mb(minibatch_index)
if (iteration+1) % num_training_batches == 0:
validation_accuracy = np.mean(
[validate_mb_accuracy(j) for j in xrange(num_validation_batches)])
print("Epoch {0}: validation accuracy {1:.2%}".format(
epoch, validation_accuracy))
if validation_accuracy >= best_validation_accuracy:
print("This is the best validation accuracy to date.")
best_validation_accuracy = validation_accuracy
best_iteration = iteration
if test_data:
test_accuracy = np.mean(
[test_mb_accuracy(j) for j in xrange(num_test_batches)])
print('The corresponding test accuracy is {0:.2%}'.format(
test_accuracy))
print("Finished training network.")
print("Best validation accuracy of {0:.2%} obtained at iteration {1}".format(
best_validation_accuracy, best_iteration))
print("Corresponding test accuracy of {0:.2%}".format(test_accuracy))
#### Define layer types
class ConvPoolLayer(object):
"""Used to create a combination of a convolutional and a max-pooling
layer. A more sophisticated implementation would separate the
two, but for our purposes we'll always use them together, and it
simplifies the code, so it makes sense to combine them.
"""
def __init__(self, filter_shape, image_shape, poolsize=(2, 2),
activation_fn=sigmoid):
"""`filter_shape` is a tuple of length 4, whose entries are the number
of filters, the number of input feature maps, the filter height, and the
filter width.
`image_shape` is a tuple of length 4, whose entries are the
mini-batch size, the number of input feature maps, the image
height, and the image width.
`poolsize` is a tuple of length 2, whose entries are the y and
x pooling sizes.
"""
self.filter_shape = filter_shape
self.image_shape = image_shape
self.poolsize = poolsize
self.activation_fn=activation_fn
# initialize weights and biases
n_out = (filter_shape[0]*np.prod(filter_shape[2:])/np.prod(poolsize))
self.w = theano.shared(
np.asarray(
np.random.normal(loc=0, scale=np.sqrt(1.0/n_out), size=filter_shape),
dtype=theano.config.floatX),
borrow=True)
self.b = theano.shared(
np.asarray(
np.random.normal(loc=0, scale=1.0, size=(filter_shape[0],)),
dtype=theano.config.floatX),
borrow=True)
self.params = [self.w, self.b]
def set_inpt(self, inpt, inpt_dropout, mini_batch_size):
self.inpt = inpt.reshape(self.image_shape)
conv_out = conv.conv2d(
input=self.inpt, filters=self.w, filter_shape=self.filter_shape,
image_shape=self.image_shape)
pooled_out = downsample.max_pool_2d(
input=conv_out, ds=self.poolsize, ignore_border=True)
self.output = self.activation_fn(
pooled_out + self.b.dimshuffle('x', 0, 'x', 'x'))
self.output_dropout = self.output # no dropout in the convolutional layers
class FullyConnectedLayer(object):
def __init__(self, n_in, n_out, activation_fn=sigmoid, p_dropout=0.0):
self.n_in = n_in
self.n_out = n_out
self.activation_fn = activation_fn
self.p_dropout = p_dropout
# Initialize weights and biases
self.w = theano.shared(
np.asarray(
np.random.normal(
loc=0.0, scale=np.sqrt(1.0/n_out), size=(n_in, n_out)),
dtype=theano.config.floatX),
name='w', borrow=True)
self.b = theano.shared(
np.asarray(np.random.normal(loc=0.0, scale=1.0, size=(n_out,)),
dtype=theano.config.floatX),
name='b', borrow=True)
self.params = [self.w, self.b]
def set_inpt(self, inpt, inpt_dropout, mini_batch_size):
self.inpt = inpt.reshape((mini_batch_size, self.n_in))
self.output = self.activation_fn(
(1-self.p_dropout)*T.dot(self.inpt, self.w) + self.b)
self.y_out = T.argmax(self.output, axis=1)
self.inpt_dropout = dropout_layer(
inpt_dropout.reshape((mini_batch_size, self.n_in)), self.p_dropout)
self.output_dropout = self.activation_fn(
T.dot(self.inpt_dropout, self.w) + self.b)
def accuracy(self, y):
"Return the accuracy for the mini-batch."
return T.mean(T.eq(y, self.y_out))
class SoftmaxLayer(object):
def __init__(self, n_in, n_out, p_dropout=0.0):
self.n_in = n_in
self.n_out = n_out
self.p_dropout = p_dropout
# Initialize weights and biases
self.w = theano.shared(
np.zeros((n_in, n_out), dtype=theano.config.floatX),
name='w', borrow=True)
self.b = theano.shared(
np.zeros((n_out,), dtype=theano.config.floatX),
name='b', borrow=True)
self.params = [self.w, self.b]
def set_inpt(self, inpt, inpt_dropout, mini_batch_size):
self.inpt = inpt.reshape((mini_batch_size, self.n_in))
self.output = softmax((1-self.p_dropout)*T.dot(self.inpt, self.w) + self.b)
self.y_out = T.argmax(self.output, axis=1)
self.inpt_dropout = dropout_layer(
inpt_dropout.reshape((mini_batch_size, self.n_in)), self.p_dropout)
self.output_dropout = softmax(T.dot(self.inpt_dropout, self.w) + self.b)
def cost(self, net):
"Return the log-likelihood cost."
return -T.mean(T.log(self.output_dropout)[T.arange(net.y.shape[0]), net.y])
def accuracy(self, y):
"Return the accuracy for the mini-batch."
return T.mean(T.eq(y, self.y_out))
#### Miscellanea
def size(data):
"Return the size of the dataset `data`."
return data[0].get_value(borrow=True).shape[0]
def dropout_layer(layer, p_dropout):
srng = shared_randomstreams.RandomStreams(
np.random.RandomState(0).randint(999999))
mask = srng.binomial(n=1, p=1-p_dropout, size=layer.shape)
return layer*T.cast(mask, theano.config.floatX)
問題
-
現在、SGDの関数では訓練のエポック数をユーザが手入力するようになっています。
しかし以前議論したように、訓練のエポック数を自動的に決める方法として早期打ち切りが知られています。
そこで、network3.pyを修正して、この早期打ち切りを実装してください。
-
任意のデータセットに対して、精度を出力する関数をNetworkに追加してください。
-
SGD関数を修正して、学習率 $\eta$ がエポック数の関数になるようにしてください。
ヒント: この問題にしばらく取り組んだら、このリンクの議論を見るとよいでしょう。
-
この章の前半で、訓練データに(小さい)回転やせん断、並進移動を加えることで、訓練データを拡張するテクニックを紹介しました。
network3.pyを修正して、上記のテクニックを取り入れてください。
巨大なメモリを持っていない場合には、拡張データセット全体を生成するのは実用的ではありません。
そのときは別のアプローチを考えてください
-
ネットワークを記録、再生する機能をnetwork3.pyに加えてください。
-
現在のコードの欠点は、診断ツールが少ないことです。
ネットワークの過適合の度合いを簡単に把握できる診断ツールを考えて、実装してください。
-
ReLUの初期化手続きは、シグモイド(とtanh)のニューロンの場合と同じ手続きを使っています。
以前の初期化の議論はシグモイド関数に特有のものでした。
(出力も含め)全体がReLUから構成されるネットワークを考えてみてください。
ネットワーク中の全ての重みを定数 $c > 0$ でスケーリングすると、単に出力が $c^{L-1}$ 倍されることを示してください。
ただし、 $L$ は層の数とします。
最終層がソフトマックス関数になると、これはどのように変化するでしょうか?
シグモイドの初期化方法をReLUに適用するのはどう思いますか?
もっと良い初期化方法を思いつきますか?
注意:これは自由回答の問題です。答えは決まっていません。
しかし、この問題を考えてみることで、ReLUを含むネットワークに対する理解が深まるでしょう。
- 勾配が不安定になる問題への分析 は、以前の章でシグモイドニューロンに対して実施しました。 ReLUから構成されるネットワークになると、この分析はどう変化するでしょうか? 勾配が不安定となる問題を回避するための、ネットワークを修正する良い方法を思いつきますか? 注意: 「良い」方法を探すのは研究課題です。 目的を達成する修正は実際には簡単に思いつきます。 しかし、本当に「良い」テクニックかどうかは私は深く調べ切っていません。
画像認識の近年の進展
1998年、MNISTが生まれた年には、当時の最新のワークステーションを使ったとしても、ネットワークの訓練に数週間かかっていました。 その時の精度を、現在GPUを使うと一時間以内に達成してしまいます。 したがってMNISTは現在の技術の前では、もはや問題として物足りなくなってしまったと言えます。 現在では、より難しい画像認識問題を研究の課題とするようになりました。 このセクションでは、近年のニューラルネットワークを使った画像認識の研究を概観します。
このセクションは本書の大部分と趣向が異なります。 これまで本書では、長く通用するアイデアをテーマとして扱ってきました。 例えば、逆伝播、正規化、畳込みネットワークなどです。 今から記述していくような、長期的には価値が不明な流行っている知見を避けようとしてきたのです。 科学の世界では、流行りというのはすぐに移り変わり、影響力が薄いものです。 このことから考えると、懐疑的な人は次のように述べるでしょう。 「ええとつまり、近年の画像認識の成果は結局、流行りものですよね? 2、3年後には、物事は移り変わっているはずです。 したがって最新の結果というものは、最先端で競争する専門家のような限られた人にとってのみ、意味のあるものですね? だとしたら、私たちがなぜ議論する必要があるのですか?」
最新論文の細かい結果の重要性は徐々に薄れていく、ということに関しては、懐疑論者は正しいです。 とは言うものの、ここ数年、途轍もなく難しい画像認識問題に深層ネットワークが挑み、その素晴らしい結果が立て続けに発表されています。 2100年の、コンピュータビジョンの歴史を綴る歴史家のことを想像してください。 彼らはきっと、2011年から2015年(とさらに数年)を、深層畳込みネットワークによるブレークスルーの時代と位置づけるでしょう。 それは2100年になっても、深層畳込みネットワークが通用するか否かとは無関係です。 もちろん、ドロップアウトやReLUなどのアイデアが使用されているかどうかも関係ありません。 それは、歴史の中でまさに今、重大な進化が起きているということを意味するのです。 原子の発見や抗生物質の発明を目撃しているようなものだと思います。 これは、歴史的な規模の発明と発見と私は信じています。 したがって、詳細には踏み込みませんが、この瞬間も新たに発見されているアイデアを確認しておくことは重要なのです。
2010年のLRMD論文: 2012年のStanfordとGoogleの研究者による論文からまず始めましょう* *2012年のQuoc Le, Marc'Aurelio Ranzato, Rajat Monga, Matthieu Devin, Kai Chen, Greg Corrado, Jeff Dean, Andrew NgによるBuilding high-level features using large scale unsupervised learning。 この論文で扱われているネットワークの詳細な構造は、これまで学んできた深層畳み込みネットワークと多くの点で異なります。 しかし、大まかな視点で見ると、同じアイデアに基づいていることが分かります。。 この論文を、最初の4人の著者の苗字からLRMDと呼びます。 LRMDはニューラルネットワークを用いてImageNetという画像分類問題を解いています。 ImageNetは画像認識の難問です。 彼らが使用した2011年のImageNetのデータは、2万カテゴリに分類された1600万枚のフルカラー画像でした。 これらの画像はウェブ上で集められ、Amazon Mechanical Turkのサービスにより分類されたものです。 これがImageNetの画像の例です* *これらは2014のデータセットのものです。 2011年のデータとは少し異なります。 しかし質的にはほとんど同じです。 ImageNetの詳細は、Jia Deng, Wei Dong, Richard Socher, Li-Jia Li, Kai Li, Li Fei-Feiによる2009年のImageNetの論文、 ImageNet: a large-scale hierarchical image databaseを参照してください。。




これらの画像の分類クラスはそれぞれ、玉縁装飾かんな、キュウリ科の植物の褐色根腐れを引き起こす菌類、加熱された牛乳、線虫です。 問題を試したいのであれば、ImageNetの手工具のページをお薦めします。 上記サイトでは、玉縁装飾かんな、木口用かんな、面取りかんなを始め、10種類程度のかんなの分類があります。 あなたがどうかは分からないですが、私はこれらの道具を自信を持って区別できません。 これは明らかにMNISTよりも難しい画像認識問題です! LRMDのネットワークはImageNet画像に対して、 $15.8$ %の分類精度を得ています。 あまり精度が良くないように聞こえるでしょう。 でも、LRMDより以前の最高結果は $9.3$ %だったのです。 そこから考えると大きな進展です。 この進展は、ImageNetのような難しい画像認識問題に対して、ニューラルネットが強力なアプローチであることを示しています。
2012年のKSH論文: 2012年に Krizhevsky, Sutskever, Hinton(KSH)がLRMDの研究を追って論文*を出しました *2012年のAlex Krizhevsky, Ilya Sutskever, Geoffrey E. HintonによるImageNet classification with deep convolutional neural networks。 KSHは、ImageNetデータのサブセットを使って、深層畳み込みニューラルネットワークの訓練とテストをしました。 このサブセットは、機械学習の人気の大会であるILSVRC(the ImageNet Large-Scale Visual Recognition Challenge)から引用したものです。 この大会で使用されるデータセットを用いると、他の最先端アプローチと比較することができます。 ILSVRC-2012の訓練データ・セットは、1000の分類クラスからなる120万のImageNet画像です。 検証とテストのデータは、1000の分類クラスからなるそれぞれ5万と15万の画像です。
ILSVRCの難しい点はImageNetの画像が複数の物体を含んでいることです。 ラブラドールレトリバーがサッカーボールを追いかけている画像を思い浮かべてください。 ImageNetによる「正しい」分類クラスは、きっとラブラドールレトリバーでしょう。 ここで、この画像をサッカーボールと分類した時に、このアルゴリズムはペナルティを受けるべきでしょうか? この曖昧性を考慮して、実際のImageNetの分類は $5$ つ選んだ分類の中に正解があれば、アルゴリズムは正しいと判定することになっています。 この上位 $5$ の分類を使う基準に則ると、KSHの深層畳み込みネットワークは $84.7$ %の精度を達成しています。 ちなみに次点のネットワークの精度は $73.8$ %でした。 分類の正確性の基準をもう少し厳しいものを適用すると、KSHのネットワークの分類精度は $63.3$ %となります。
KSHのネットワークは後続の研究に大きな影響を与えたネットワークであるので、今後の参考のために簡単に描写してみようと思います。 KSHの方が手が込んでいますが、本章でこれまで私たちが訓練してきたネットワークにとてもよく似ています。 KSHは深層畳み込みニューラルネットワークであり、2台のGPU上で訓練を行っています。 2台のGPUを使用した理由は、使用しているGPU(NVIDIA GeForce GTX580)に原因があります。 ネットワーク全体を保持するためには、このGPUのオンチップメモリが足りないのです。 そのため、ネットワークを二分割して2台のGPUに分けて搭載しています。
KSHのネットワークには7つの隠れ層があります。 前方の $5$ つの隠れ層は畳み込み層(幾つかはMaxプーリング付き)で、次の $2$ 層は全結合層です。 出力層は $1,000$ ユニットからなるソフトマックス層で、 $1,000$ の分類クラスに対応しています。 下図がKSHの論文*から引用したネットワークのスケッチです *Ilya Sutskeverに感謝します。。 詳細は下に記述します。 多くの層が $2$ つのGPUに対応するために $2$ 部分に分割されていることに注意してください。
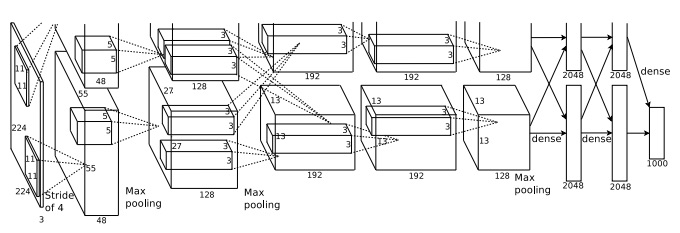
入力層は、 $3 \times 224 \times 224$ ニューロンを含み、 $224 \times 224$ の画像のRGB値を表します。 以前述べたように、ImageNetの画像は解像度が異なることを思い出してください。 ニューラルネットワークの入力層のサイズは固定なので、このままでは問題が起きます。 そこで、KSHは各画像を拡大縮小して、短辺が長さ $256$ となるように調整しています。 次に、その画像の中央 $256 \times 256$ の領域を切り取ります。 最後に、その $256 \times 256$ 領域の中から、ランダムに $224 \times 224$ の部分画像(水平反転も含む)を抜き出します。 このランダムに抜き出す操作により、訓練データを拡張し、過適合を防いでいます。 この一連の操作はKSHのような巨大なネットワークの場合、有効です。 $224 \times 224$ の画像がネットワークの入力に使われています。 大抵の場合、抜き出された画像は目的の物体を含んでいるはずです。
KSHの隠れ層の話に移ります。 1つ目の隠れ層はMaxプーリング付きの畳み込み層です。 この層はサイズが $11 \times 11$ の局所受容野を、ストライド長さ $4$ ピクセルで使います。 全体で $96$ の特徴マップとなります。 特徴マップは各 $48$ の2グループに分割され、始めの $48$ の特徴マップは片方のGPUに置かれ、後半の $48$ の特徴マップはもう片方のGPUに置かれます。 この層含めて後層でも、Maxプーリングは $3 \times 3$ の領域で行われます。 しかしプーリング領域は重複が許されており、実際 $2$ ピクセルしか離れていません。
2つ目の隠れ層もMaxプーリング付きの畳み込み層です。 $5 \times 5$ の局所受容野を使い、全体で $256$ の特徴マップを持ち、各GPUに $128$ ずつ分割され置かれます。 ここで特徴マップは、前層の出力の $96$ チャネル全てを利用するのではなく、 $48$ の入力チャネルのみ使うことに注意してください (これは通常の操作ではありません)。 なぜかと言うと、同じGPUからしか入力を受け取れないからです。 この点で、これまで私たちが学んできた畳み込み層とは異なります。 ただし、根底に流れる基礎的なアイデアはやはり同じです。
3、4、5層目の隠れ層も畳込み層ですが、前層までと異なりMaxプーリングは行いません。 各パラメータは次のようになっています。 (3) 特徴マップ $384$ 個、局所受容野のサイズ $3 \times 3$ 、入力チャネル $256$ 、 (4) 特徴マップ $384$ 個、局所受容野のサイズ $3 \times 3$ 、入力チャネル $192$ 、 (5) 特徴マップ $256$ 個、局所受容野のサイズ $3 \times 3$ 、入力チャネル $192$ 、 3層目は、特徴マップが全ての入力チャネルを使うために、(図に示すように)GPU間通信を行うことに注意してください。
6、7層目の隠れ層は $4,096$ のニューロンからなる全結合層です。
出力層は $1,000$ ユニットのソフトマックス層です。
KSHのネットワークは多くのテクニックを利用しています。 シグモイドやtanhを活性化関数に使う代わりに、ReLUを使って訓練を高速化しています。 もともと巨大な訓練データセットを使っているとはいえ、KSHのネットワークには約6000万のパラメータがあるので、過適合しやすいです。 これを克服するために、上述の通りランダムに抜き出す戦略により、訓練データを拡張したのです。 さらにL2正規化の一種や、ドロップアウトを用いて過適合を抑制しています。 ネットワークの訓練は、モメンタムを用いたミニバッチ確率的勾配降下法で行います。
以上がKSH論文の重要アイデアの概要です。 いくつかの詳細は省きました。 論文で確認してみてください。 またAlex Krizhevskyによるcuda-convnet(とその後継情報)を見るのもよいでしょう。 コード実装に関するたくさんのアイデアが載っています。 Theanoベースの実装は発表*されており、 *2014年のWeiguang Ding, Ruoyan Wang, Fei Mao, and Graham TaylorによるTheano-based large-scale visual recognition with multiple GPUs ここでそのコードが入手できます。 そのコードは複数GPUの使用するため少し複雑ですが、この章で見てきたものにそっくりです。 Caffeフレームワークの中でもKSHネットワークが実装されています。 Model Zooを見てください。
2014のILSVRC: 2012年から急激な発展が続きました。 2014年のILSVRCコンペティションを概観しましょう。 2012年の場合と同じく、訓練データは $1,000$ の分類クラスからなる $120$ 万の画像です。 正解の基準は、画像に対して分類した上位 $5$ カテゴリの中に正しいラベルが含まれていることです。 勝者はGoogle*を主体としたチームで *2014年のChristian Szegedy, Wei Liu, Yangqing Jia, Pierre Sermanet, Scott Reed, Dragomir Anguelov, Dumitru Erhan, Vincent Vanhoucke, Andrew RabinovichによるGoing deeper with convolutions、 $22$ 層の深い畳み込みネットワークを使用していました。 彼らは自身のネットワークを、LeNet-5に対するオマージュとしてGoogLeNetと名付けました。 GoogLeNetは上位5分類基準の精度で評価すると $93.33$ %でした。 これは2013年の勝者の記録(Clarifaiは $88.3$ %)と2012年の勝者の記録(KSHは $84.7$ %)を大幅に上回っています。
GoogLeNetの $93.33$ %という精度はどのくらい良い結果なのでしょうか? 2014年に研究者がILSVRCに関するサーベイ論文*を書いています *2014年のOlga Russakovsky, Jia Deng, Hao Su, Jonathan Krause, Sanjeev Satheesh, Sean Ma, Zhiheng Huang, Andrej Karpathy, Aditya Khosla, Michael Bernstein, Alexander C. Berg, Li Fei-FeiによるImageNet large scale visual recognition challenge。。 彼らは、ILSVRCに人間が挑むとどのような精度になるか、という問題を提起しました。 これを調べるために、彼らは人間がILSVRC画像を分類するためのシステムを作りました。 著者の1人であるAndrej Karpathyが有益な ブログの投稿を行っています。 その内容は、人間がGoogLeNetのパフォーマンスにたどり着くのは難しいというものでした。
...画像に対して1000のカテゴリの中から5カテゴリを選んでラベリングするタスクは極めて難しかったです。 ILSVRCに日常的に取り組んでいて、分類に馴染みがある研究所の友人にとってさえ難しいものでした。 一番初めは、Amazon Mechanical Turkのサービスを利用しようと考えていました。 その後、学部生にバイトさせる方針に切り替えました。 最後には、私たちの研究所の(ラベリングを専門とする)人たちの中で組織を作ることにしました。 そこで、GoogLeNetの予測のために使ったインターフェースに修正を加えて、分類のカテゴリ数を1000から100へ減らしました。 それでもまだまだ難しすぎました。 皆、分類を間違えて 13-15% の誤差を出し続けたのです。 結局、GoogLeNetの精度に接近するためには、私自身が長時間座り続けて長く辛い訓練を行った上で、注意深くラベリングするしかない...と気づきました。 訓練し始めた当初は、分類作業を1分に1回しかできませんでした。 しばらく経つと、次第に高速にできるようになり...画像によってはすぐに認識できる状態となりました。 一方、画像(細かい犬種や鳥の種類、猿の種類を示す画像など)によっては、集中して数分取り組まないといけませんものもありました。 しかし更に時間が経つと、訓練画像をもとにして...犬種の識別など、かつて難しかったタスクを容易に行えるようになりました。 GooLeNetは分類誤差が 6.8% でしたが、... 私の分類誤差は最終的には 5.1% となり、約 1.7% ポイント勝りました。
つまり、専門家の人間が苦痛を伴う努力をして初めて、深層ニューラルネットワークを僅かに上回れるということです。 実際、2人目の専門家は、サンプル数の少ない訓練画像で訓練して挑んだものの、$12.0$ %の誤差までしか到達できなかったとKarpathyは報告しています。 これはGoogLeNetの性能に大きく劣ります。 間違えた問題の半数は、選択肢にさえ真のラベルを選べなかったそうです。
この報告は驚異的です。 この研究以降、実は幾つかのチームが 5.1% を超える結果を報告しています。 これらの結果を受けて、「システムが人間を超える視覚を手に入れた」とメディアで報道がなされました。 たしかに結果は本当に素晴らしいものですが、注意することとして、「人間を超える視覚を手に入れた」、というのは誤解です。 ILSVRCはとても制約の大きい問題です。 ウェブから集めた画像を分類しているので、様々な応用目的で使う画像とは必ずしも一致しません。 もちろん評価指標である、上位 $5$ を基準にするというのも非常に恣意的です。 画像認識、さらに広く言うとコンピュータビジョンの問題を完全に解いたとはまだとても言えないのです。 ただし、難問に対して、たった数年でこの結果が得られたというのは、とても励みになります。
他の活動: これまでImageNetを見てきました。 しかし、他にもニューラルネットワークを使用して画像認識する活動があります。 興味深い近年の研究結果を簡単に紹介します。
Googleによって生まれた実践的な結果があります。 彼らは深層畳み込みネットワークを、Google Street Viewの景色の中の数字認識の問題に適用*しました *2013年のIan J. Goodfellow, Yaroslav Bulatov, Julian Ibarz, Sacha Arnoud, Vinay ShetによるMulti-digit Number Recognition from Street View Imagery using Deep Convolutional Neural Networks。 論文の中では、1億の路地番号を検知して自動的に文字に起こすタスクが、人間と同等の精度で行われたと報告されています。 さらに、このシステムは非常に高速です。 Street Viewのフランス国内の全ての画像において、路地番号全てを1時間以内に文字に起こしたのです! 「生成した路地番号のデータセットを利用すると、Google Mapの地理情報の質が驚異的に向上しました。他の地理情報源を従来持たなかった幾つかの国では、特に影響が大きかったです」と彼らは述べています。 また、「短文の視覚文字認識の問題をこのモデルでは解決したと思っています。このモデルは多くのアプリケーションに利用できます」とも述べています。
これらは素晴らしい結果だと私も思っています。 しかし、別の研究では、私たちは本質をまだ理解できていないという指摘がなされています。 例えば、2013年の論文* *2013年のChristian Szegedy, Wojciech Zaremba, Ilya Sutskever, Joan Bruna, Dumitru Erhan, Ian Goodfellow, Rob FergusによるIntriguing properties of neural networks。 では、深層ネットワークが盲点を持ち、挙動が不安定となる様子が示されています。 下図を見てください。 左は、ネットワークによって正しく分類されたImageNet画像です。 右は、少し外乱(中央の画像)が挿入された画像です。 ネットワークは右の画像を誤って分類しました。 特別な画像だけでなく、どの画像にもそのような"adversarial"な画像が存在すると著者は指摘しています。

この結果には戸惑います。 論文では、KSHのネットワークの場合をもとにネットワークを組み立てていました。 KSHのネットワークの種類は、とても幅広く使われているのです。 そのようなニューラルネットワークの計算する関数は原理的に連続的であるはずなのに、 上記の結果は極端な非連続性を示すものでした。 しかもこれは、私たちの直感に反する非連続性です。 これは気がかりです。 何が非連続性の要因なのかがまだ良くわかっていないのです。 誤差関数の何かに関係しているのでしょうか? 活性化関数? ネットワークの構造? それとも他の何かでしょうか? まだ分かっていません。
実は、これらの結果に悲観する必要はありません。 adversarialな画像は普遍的に存在しますが、実践では発生しにくいのです。
adversarialな存在はネットワークの高い汎化性能に矛盾するように思えます。 実際、ネットワークが汎用性を獲得できた場合、通常の画像と一見区別できないようなadversarialな存在によって騙されうるのでしょうか? これに対する反論は、adversarialな画像はめったに発生しないため、テストセットの中には観測されないというものです。 しかし、テストセットは有理数のように詰まっているため、本質的にはどんなテストケースにも存在するはずです。
このような類の結果が近年発見されるのは、本質的にニューラルネットワークを理解していないことの現れでしょう。 もちろん、このような結果の発表されることで、追跡調査が盛んに行われ、研究が進みます。 他にも例えば、最近の論文* *2014年のAnh Nguyen, Jason Yosinski, Jeff CluneによるDeep Neural Networks are Easily Fooled: High Confidence Predictions for Unrecognizable Images では、人間にはホワイトノイズに見えるのに、ネットワークは確信を持って既知のカテゴリに分類するような画像を生成する結果が報告されています。 ニューラルネットワークとその画像認識法を理解するまでにはまだまだ時間がかかりそうです。
しかし現状を俯瞰すると、励みになる結果が多いです。 ImageNetのようにとても難易度の高いベンチマークに対する急速な進展がありました。 また、StreetViewの路地番号を認識するという現実世界の問題に対処する例も確認しました。 これらは励みになります。 ただし、ベンチマークに対する良い結果や現実への応用を追うのみでは不十分だと思います。 まだ、adversarialな画像の例など、私たちがほとんど理解できていない本質的な現象があります。 そのような本質的な問題は、現在も研究されている途中であり、 画像認識の問題を完全に解くには、まだまだ発展途上だと言えます。 別の言い方をすると、今後の研究には余地がたくさん残っており、課題としてはとても魅力的なのです。
深層ニューラルネットワークに対する他のアプローチ
本書では、MNISTの数字分類というただ一つの問題に専念してきました。 MNISTの問題は味わい深くて、重要なアイデアを理解することができました。 それは確率的勾配降下法や、逆伝播、畳込みネットワーク、正規化などです。 しかし、この問題の扱う領域は広くはありません。 ニューラルネットワークの文献を読むと、これまで議論に登場しなかった多くのアイデアに出会うはずです。 例えば、再帰型ニューラルネットワークやボルツマンマシン、生成モデル、転移学習、強化学習、 $\ldots$ ! ニューラルネットワークはとても広い分野なのです。 しかし、その多くの重要なアイデアは、実を言うとこれまで既に議論してきたアイデアの応用でしかありません。 なので、少しの努力で理解できるはずです。 このセクションでは、あなたのまだ知らないニューラルネットワークについて少しお見せしましょう。 本書の範囲を越えてしまうため、詳しい議論や網羅的な議論は行いません。 むしろ、各概念を直感的に理解できるように、これまで学んできたことに関連させて学んでいきます。 セクションを通じて、他のソースへのリンクを示しておきます。 このリンクを辿れば、さらに学ぶことができます。 もちろん、リンクの多くは今後すぐに古びてしまい、最先端の文献を常に探すようになるでしょう。 それでも、根底のアイデアは永続的に残るはずです。
再帰型ニューラルネットワーク (RNN): これまで使ってきたフィードフォワードのネットワークでは、後方のニューロンの活性化を決める入力は1つでした。 これはとても静的な構造です。 ネットワークの全ては固定され、まるで凍結された結晶のようです。 しかし、動的に変化し続けるネットワーク要素を想定することもできます。 例えば、隠れ層の振る舞いが、1つ前の隠れ層の活性化によってのみ決まるのではなく、 さらに以前の活性化にも影響されるような場合も考えられます。 実際、あるニューロンの活性化が、そのニューロン自身の以前の活性化により定義されることもありそうです。 単なるフィードフォワードネットワークでは、そんなことは起きません。 さらに別の場合を考えてみると、隠れ層や出力層の活性化がネットワークの現在の入力だけでなく、もっと以前の入力によっても影響されるパターンも想定できます。
このような時間経過を考慮に入れたニューラルネットワークは、 再帰型ニューラルネットワークもしくはRNNとして知られています。 この再帰型ネットワークの数学的な定式化は、色々なやり方があります。 WikipediaのRNNのページを眺めると数学的モデルの雰囲気が掴めます。 この執筆段階では、上記ページには13以上の異なるモデルが掲載されています。 数学的詳細は置いておき、RNNを大雑把に表現すると、時間経過による動的変化の概念が含まれるニューラルネットです。 このモデルは時間により変化するデータの分析や処理に役立ちます。 そのようなデータや処理は、音声や自然言語などの問題に自然と含まれています。
現在のRNNの使われ方の1つは、アルゴリズムの概念やチューリングマシンやプログラミング言語などの概念を、ニューラルネットワークに学習させるというものです。 2014の論文では、 (とても、とてもシンプルな!)Pythonプログラムの文字列を入力としてRNNに渡して、プログラムの出力を予測するのにRNNが使われました。 砕けた言い方をすると、そのネットワークはPythonプログラムを「理解する」ことを学んでいます。 同じく2014年の論文では、 ニューラルチューリングマシン(NTM)と呼ばれるものを開発するための足がかりとして、RNNを使っていました。 このNTMは、勾配降下によって汎用計算機の構造を学習するものです。 彼らは、NTMを訓練して、ソートやコピーなどの簡単な問題に対するアルゴリズムを推測させました。
現状では、これらはシンプルすぎるトイモデルにとどまっています。 print(398345+42598)というPythonプログラムを実行することを学習しただけでは、 一人前のPythonインタープリターとは言えません。 このアイデアを推し進めると、何が実現できるようになるかは明らかではありません。 しかし、結果は実に面白いです。 歴史的には、ニューラルネットワークは既存のアルゴリズムによるアプローチが手を焼いていたパターン認識問題を上手く解決してきました。 対照的に、既存のアルゴリズムによるアプローチは、ニューラルネットワークが得意でない問題を上手く対処できます。 今日の誰も、ウェブサーバやデータベースのプログラムにニューラルネットワークを使いません! ニューラルネットワークと伝統的なアルゴリズムによるアプローチの強みを両方取り入れたモデルが作れれば、素晴らしいと思います。 RNNやRNNに端を発するアイデアはきっと、その目標に向けた良い足がかりとなるでしょう。
RNNは他にも多くの問題に利用されています。 その中でも特に音声認識において、有効活用されています。 例えば、RNNをもとにしたアプローチは 音素認識の精度向上に貢献しています。 また、会話中の言語モデルの改善にも寄与しています。 言語モデルが良ければ、発音の似ているフレーズ間でも区別できます。 例えば、言語モデルにより"to infinity and beyond" の方が "two infinity and beyond"よりも起きやすいことが分かります。 RNNは言語に関するベンチマークでも、貢献してきたのです。
これらは、深層ニューラルネットワークの音声認識における成果の一部です。 例えば、他の深層ネットワークに基づくアプローチは 大語彙連続音声認識(LVCSR)で驚異的な結果 を残しました。 また、深層ネットワークベースの別のシステムはGoogleの Androidオペレーティングシステムに採用されるほど精度が高いです (関連する技術動向は Vincent Vanhouckeによる2012から2015の論文を参照してください)。
RNNによって実現可能な具体例を述べてきましたが、どう実現するかについては触れてきませんでした。 フィードフォワードのネットワークで学んできたアイデアがRNNでも同様に使われているので、 きっとあなたに驚きはないでしょう。 勾配降下法と逆伝播を単純に修正するだけで、RNNの訓練は可能となります。 他の多くのアイデアも、RNNで有効です。 例えば、正規化のテクニック、畳み込みや活性化関数、コスト関数などです。 本書で見てきた多くのテクニックが、RNNに適用可能なのです。
長期短期記憶ユニット(LSTM): RNNの難しさの1つは、モデルを訓練するのがとても大変なことです。 深層フィードフォワードネットワークよりもさらに訓練が難しいのです。 その理由は5章で議論した勾配の不安定性に起因します。 思い出してください。 これは、後ろの層に伝播するにつれ、勾配がどんどん小さくなっていくという問題でした。 これにより、前方の層ほど学習が遅くなるのです。 RNNではこの問題がさらに悪化します。 なぜかと言うと、RNNでは勾配は単に前方の層へ伝播するだけではなく、時間経過に従い後方へも伝播するからです。 ネットワークが長時間動いている場合、勾配は極めて不安定になり、学習は難しくなるでしょう。 幸運なことに、長期短期記憶ユニットとして知られるアイデアをRNNへ取り入れることができます。 このユニットは 1997年にHochreiterとSchmidhuberが、 勾配の不安定性に取り組むために考案したものです。 LSTMにより、RNNの訓練で良い結果を簡単に得ることができるようになったため、 最近の論文の多く(私が上でリンクした論文も含め)では、LSTMもしくは関連するアイデアを利用しています。
Deep Belief Network、生成モデル、ボルツマンマシン: 近年のディープラーニングの流行の発端は2006年です。 そのきっかけは、ニューラルネットワークの一種として知られるDeep Belief Network (DBN)*の訓練方法に関する論文でした。 *2006年のGeoffrey Hinton, Simon Osindero, Yee-Whye TehによるA fast learning algorithm for deep belief netsと合わせて、2006年のGeoffrey HintonとRuslan Salakhutdinovによる Reducing the dimensionality of data with neural networksを確認してください。 DBNはその後数年は影響力がありましたが、人気は徐々に衰えていきました。 その間、フィードフォワードモデルと再帰型ニューラルネットワークが流行っていきました。 現在は流行っていないのですが、DBN自体は興味深い性質を幾つか備えています。
DBNが興味を引く一つの理由は、生成モデルと呼ばれるものの一例だからです。 フィードフォワードネットワークでは、入力の活性化状態を決まることで、ネットワークの後方の層の特徴の活性化状態も決まります。 DBNのような生成モデルも、同じように使うことができます。 しかし別の使い方として、あるニューロンの特徴を特定したら、「ネットワークを逆伝播」させ、入力の活性化値を生成することができます。 もっと具体的に言うと、手書き数字について学習したDBNは、人の手書き数字のような画像を生成可能であるということです。 抽象的に言い換えると、DBNは書くことを学べるのです。 この点において、生成モデルは人間の脳のようです。 数字を読むだけでなく、数字を書くこともできるのです。 Geoffrey Hintonはこのことを、 「形状を認識するために、まず画像を生成するのです」という記憶に残るフレーズで表現しています。
DBNが好奇心をそそる2つ目の理由は、DBNで教師なし学習や半教師あり学習が可能であるからです。 例えば、画像データを入力とする学習を行う時に、訓練画像にラベルがなくても、DBNは他の画像についての有効な特徴を学習できます。 半教師あり学習は科学的にも、(もし十分上手く動作しているなら)実用的にもとても興味深いです。
こうした魅力的な性質を持っているのに、なぜDBNはディープラーニングと比べて人気がないのでしょうか? 理由の1つは、フィードフォワードモデルや再帰型ネットワークモデルが、 画像認識や音声認識のベンチマークで、目を見張るほどの成果を出したからです。 これらのモデルへ注目が集まるのも驚きはないですし、納得できます。 DBNに人気がないのは残念ですが、当然の帰結と言えます。 アイデアの市場は、しばしば勝者総取り方式であり、その瞬間において全ての注目が一部に集まる性質があります。 その時、流行っていないアイデアに取り組もうとするのは、とても難しいのでしょう。 たとえそのアイデアが、長期的には利益が出ることが明らかだったとしても。 私の個人的な意見では、DBNや他の生成モデルは、潜在的には現在よりもさらに注目を集めてよいはずです。 DBNや関連するモデルがいつの日か、現在流行のモデルよりも人気を得ても驚きません。 DBNについて入門するには、この要約を見てください。 この記事も有益です。 当然、DBNがメインではないのですが、DBNの重要な要素である制約ボルツマンマシンに関する有益な情報が含まれています。
他のアイデア: ニューラルネットワークとディープラーニングには他にどんなアイデアがあるでしょう? ええ、他にも魅力的な研究がたくさんあります。 ニューラルネットワークの研究が盛んに行われている分野として、 自然言語処理 (この有益なレビュー論文を確認してください)や、 機械翻訳、そして音楽情報学などにも驚きの応用もあります。 今挙げた以外の領域にもあります。 背景知識のギャップを埋める必要はありますが、 本書を読み終えたら、最近の研究を読み始めることができるはずです。
このセクションの締めに、特別楽しめる論文を紹介しましょう。 この論文は深層畳み込みネットワークと強化学習を組み合わせて、 ビデオゲームを上手くプレイ (こちらの追加情報も参照してください)するよう学習するものです。 畳み込みネットワークを使って、ゲームスクリーンのピクセルデータを単純化し、特徴へ変換します。 それをもとに「左へ移動する」「下へ移動する」「発泡する」などの行動を決定します。 一番興味深いのは、単一のネットワークで、7つの異なるクラシックなビデオゲームを、とても上手くプレイするよう学習したことです。 そのうち3つのゲームでは、人間の専門家のパフォーマンスで上回りました。 これは離れ業のように聞こえるでしょう。 この論文は "Playing Atari with reinforcement learning" というタイトルで注目を集めました。 定性的に考えると、このシステムは生のピクセルデータを入力とするだけです。 つまり、ゲームのルールすら知らないのです! 複雑なルールで構成される様々な環境において、単なるピクセルデータのみを入力として、高品質な意思決定を行っているのです。 極めて巧妙なのです。
ニューラルネットワークの未来
意図で駆動するユーザインタフェース: 気短な教授が、どうすればよいか分かっていない学生に次のように伝える古いジョークがあります。 「私が言うことを聞かなくていい。私の意図を読み取ってくれ」と。 昔からコンピュータは、ユーザの意図が分からず戸惑っている学生のような存在でした。 しかし、現在変化しつつあります。 私が初めてGoogle検索でスペルを間違えてしまった時に、Googleが "Did you mean [正しいクエリ]?"と伝えてきて、対応する検索結果を提示したときの驚きをまだ覚えています。 GoogleのCEOのLarry Pageは、 あなたの検索の意味を正確に理解し、まさに望むものを提供する完璧な検索エンジンについて記述を残しています。
これは意図駆動のユーザインタフェースの理想像です。 この理想像では、ユーザによる文字ベースのクエリの代わりに、ぼんやりとした入力からユーザの意図を機械学習で識別して、その意図に対して機能を提供するのです。
意図駆動のインターフェースのアイデアは、検索以外にも幅広く適用できます。 数十年以内に、何千もの会社が機械学習を使って、ユーザの真の意図を識別・行動するインターフェースを作り上げるでしょう。 私たちは意図駆動のインターフェースの早熟な例を既に目の当たりにしています。 AppleのSiri、Wolfram Alpha、IBMのWatsonや、写真やビデオに注釈をつけるシステムなどです。
これらの製品の大半は失敗するでしょう。 見事なユーザインターフェースデザインは難しいのです。 しかし、強力な機械学習技術を使うことで、素晴らしいユーザインターフェースを作り上げることを期待しています。 ユーザインターフェースのコンセプト自体がもともと悲惨だと、機械学習が素晴らしくても意味がないでしょう。 しかし、それ以外の製品は成功すると思います。 そのうち、私たちのコンピュータへの関わり方に大きな変化が起こるでしょう。 つい最近まで、2005年くらいまででしょうか、ユーザはコンピュータとやり取りするのに正確な操作を必要としていました。 実際、当時のコンピュータリテラシの意味というのは、コンピュータには想像力がないということを理解することでした。 一文字分セミコロンの位置を間違えただけで、コンピュータは意図通りに動きません。 しかし、数十年後には、上手く作動する意図駆動のユーザインターフェースが開発されることを私は期待します。 その結果、コンピュータとの関わり方が劇的に変わるでしょう。
機械学習、データサイエンス、イノベーションの好循環: もちろん、機械学習は意図駆動のユーザインターフェースだけに使われるのではありません。 注目の応用先はデータサイエンスです。 そこでは、機械学習がデータの中の「既知の未知」を発見するのに使われます。 この分野は既に流行っており、文献はたくさんあるので、私は多くを語りません。 しかし、この流行りの行き着く先について、一つ述べておきます。 長期的に見ると、機械学習でのブレークスルーはおそらく、アイデアや発明のブレークスルーではありません。 一番大きなブレークスルーは、データサイエンスか他の分野かにおいて、機械学習研究が利益を出すことだと思います。 ある会社が1ドルを機械学習研究に投資して、すぐに1ドルと10セントを回収したとすると、 多くのお金が機械学習研究につぎ込まれるでしょう。 言い換えると、機械学習は新たな巨大市場を生成し、技術の成長分野となりうるのです。 その結果、深い専門技術をもった多くのチームと、途轍もなく巨大なリソースが誕生します。 最終的に、それらが機械学習を更に促進させ、さらなる市場と機会を作り、イノベーションの好循環の図となるはずです。
ニューラルネットワークとディープラーニングの役割: 機械学習について、技術にとって新たな機会を創出するだろうとこれまで広く述べてきました。 ニューラルネットワークとディープラーニングの役割は、特にどのようなものでしょうか?
この疑問に答えるには、歴史を振り返るのが助けになるかもしれません。 1980年代は多くの実験がなされており、ニューラルネットワークに対する楽観的な見方が広がっていました。 逆伝播が広く知られるようになってからは、特に楽観的でした。 実験が減っていき、1990年代に入って、他のサポートベクターマシンなどのテクニックにバトンを渡しました。 今日、ニューラルネットワークは再び、勢いに乗っています。 様々な記録を打ち立て、多くの問題に対する他の解決法を負かしました。 しかし、明日には別の新しいアプローチが登場して、ニューラルネットワークを再び淘汰する可能性を誰が否定できるでしょうか? もしくは、代替技術がなくても、そのうちニューラルネットワークの進化は停滞するのではないでしょうか?
このような可能性を考えると、ニューラルネットワークだけを予想するよりも、広く機械学習の未来を考えるほうが簡単です。 そもそも私たちは、ニューラルネットワークを深く理解できていません。 なぜ、ニューラルネットワークは十分に汎化できるのでしょうか? パラメータ数がとても多いときに、過適合を避けるにはどうすればよいのでしょうか? 確率的勾配降下法はなぜ上手く動作するのでしょうか? データセットのサイズが変化したとき、ニューラルネットワークはどの程度上手く動作するでしょうか? 例えば、ImageNetが $10$ 倍に拡張された場合、他の機械学習技術と比較して、ニューラルネットワークの性能は向上するでしょうか?それとも低下するでしょうか? これらは全てシンプルで本質的な疑問です。 そして現在、私たちはこれらの疑問への答えを持ち合わせていません。 ですので、機械学習の未来におけるニューラルネットワークの役割を述べるのは難しいのです。
1つ予測します。 ディープラーニングは定着すると私は思います。 階層的な概念を学習する能力や、層を組み立てて抽象化を行う能力は、世界を構成している本質そのものだと思います。 これは、明日のディープラーニングのモデルが、今日のモデルと同じであることを意味しているのではありません。 構造の中の構成要素や学習アルゴリズムに、大きな進展があるはずです。 それはきっと、あまりに目覚ましい変化なので、その結果のシステムがニューラルネットかどうかをもはや気にしていないと思います。 しかし、きっとディープラーニングは使われているでしょう。
ニューラルネットワークとディープラーニングはすぐに人工知能となるか? 本書ではニューラルネットワークを画像分類など特定の目的に使ってきました。 私たちの野望を大きくして、尋ねてみましょう。 汎用に考えるコンピュータになりえますか? ニューラルネットワークとディープラーニングは、(汎用)人工知能(AI)の問題を解けますか? そしてその場合は、ディープラーニングがさらに発展すれば、すぐに汎用AIを実現できますか?
これらの疑問に対して包括的に取り組むためには、別の本を書かなくてはいけません。 代わりに、一つ考察してみましょう。 この考察は、コンウェイの法則として知られるアイデアに基づいています。コンウェイの法則とは、次のことを主張しているものです。
システムを設計する組織は、その構造をそっくり真似た構造の設計を生み出してしまう。これは例えば、ボーイング747航空機の設計が、当時のボーイング社と業者の組織的な構造を反映していることを示唆します。 もしくは、さらにシンプルな具体例として、複雑なソフトウェアアプリケーションを作る会社を考えてみます。 アプリケーションのダッシュボードに、ある機械学習アルゴリズムを取り入れようとする場合、 ダッシュボードの製作者は、その会社の機械学習の専門家と話をした方がよいでしょう。 コンウェイの法則は、この例を大規模にしたものに相当します。
コンウェイの法則を初めて聞いた時、多くの人は「当たり前でしょ?」と反応するか、「間違ってない?」と反応します。 コンウェイの法則が間違っている、という二つ目の指摘に対して意見を述べさせてください。 この指摘の背景にはきっと、次のような質問が想定されているのでしょう。 「ボーイングの経理部署が、747の設計のどこに現れていますか?」、 「管理部署はどこですか?」、 「ケータリングを行う部署は?」と。 確かに、これらの組織部署は747のどこにも、現れていません。 しかし、コンウェイの法則における組織とは、設計とエンジニアリングに明らかに関わる部署のみを意図していると理解すべきなのです。
コンウェイの法則が、平凡で当たり前のことであるという指摘はどうでしょうか? この指摘は部分的には正しい気がします。 しかし、人材配置に失敗している組織に対しては、コンウェイの法則は成り立たないと思っています。 新製品を開発するチームに、年配者しかいなかったり、逆に若者のみで専門性を持つものがいなかったりする状況があります。 これは単純に、製品のターゲットと開発チームとのミスマッチです。 時に人がこの法則を無視して人材配置する場合があるのです。
コンウェイの法則は、私たちが構成要素とその組立て方をよく理解している、システムの設計とエンジニアリングに適用されます。 人工知能の開発に直接には適用できません。 なぜかと言うと、AIはまだそのような問題ではないからです。 どんな構成要素からなるのか知りません。 実際、AIに関する基礎的な問いすら分かっていないのです。 つまり、現時点でAIは工学の問題というよりは、科学の領域の問題と言えます。 ジェットエンジンや空気力学の原理を知らない状態で、747を設計する状況を想像してください。 あなたは、どんな種類の専門家を組織に雇えばいいか分からいないでしょう。 Wernher von Braunは「何をしているのか分かっていない場合には、基礎研究こそ行うべきである」と述べています。 さて、工学ではなく科学の問題に適用できるバージョンのコンウェイの法則というのはあるのでしょうか?
この問いに対する洞察を得るために、薬の歴史を考えてみてください。 古代において、薬はガレノスやヒポクラテスら体全体を研究する専門家の領域でした。 しかし、知識が蓄積されて膨大になるにつれ、徐々に領域が細分化されていきます。 その過程で、私たちは多くの奥深い発見をしてきました * *「深い」と重ねてしまい申し訳ありません。 「深い」の意味の正確な定義を私はしませんが、大ざっぱ言うと研究分野全体に必要な教養のようなものを意図しています。 逆伝播のアルゴリズムと胚種説はどちらもその好例です。 。 例えば、胚種説のような理論や、抗生物質の作用や、心、肺、静脈や動脈による心臓血管の形成などを考えてみてください。 そのような深い洞察はやがては、疫学、免疫学、心臓血管系の学問などの部分的な分野となりました。 したがって、私たちの知識の構造は、薬学の社会的構造を形作ったのです。 これは免疫学においては、とても画期的なことでした。 免疫系の存在に気づき、免疫系を研究する価値を見出したのは深い洞察からでした。 そのようにして今、薬学という分野があるのです。 専門家がいて、会議があって、賞までもあります。
これは科学が確立するときに繰り返される普遍的なパターンです。 薬学だけでなく、物理学、数学、化学でも同じです。 そんな分野でも初めは、深いアイデアを2、3個だけ伴っていました。 黎明期の専門家は、そのアイデアの全てを使いこなします。 しかし時間が経つと、アイデアは一枚岩でなくなります。 深いアイデアが新たに発見され、1人ではとても扱いきれなくなります。 結果的に、その分野の社会構造は再編され、アイデアごとに分割されます。 一枚岩の代わりに、分野の中に分野がある構造となり、複雑かつ再帰的で自己言及的な社会的構造となります。 その組織は、私たちの深い洞察を反映するのです。 つまり、私たちの知識は科学の社会的構造を形成します。 しかし一方で、社会的構造は、私たちの発見を邪魔したり促進したりします。 これは科学におけるコンウェイの法則のアナロジーです。
さて、この話がディープラーニングやAIと何の関係があるのでしょうか?
ええと、AIの黎明期には、人々は次のようなやり取りをよく行っていました。 「そんなに難しくないよ、"超特別な武器"を俺たちは既に持ってるんだから」と一方が言うと、 「"超特別な武器"じゃあまだ全然ダメだよ」と否定するというものです。 ディープラーニングは、同様の話題に使われる"最新の超特別な武器"です* *興味深いことに、否定されている人はしばしばディープラーニングの最先端の人ではありません。 例えば、下記のYann LeCunによる 思慮に満ちた投稿を見てください。 この内容は先ほどの主張とは全然異なります。 。 この主張の昔のバージョンでは、論理やProlog(非手続き型プログラミング言語)、エキスパートシステムなど、その時代の強力なテクニックが使われていました。 そのような主張に伴う重大な欠陥は、その"超特別な武器"がいかに強力かを示すことができないことです。 もちろん、ここまで1章分を費やして、ディープラーニングがとんでもない難問を解く様子を確かめました。 非常に刺激的で将来有望に見えます。 しかし、それはPrologや Eurisko、当時のエキスパートシステムにも同じことが言えます。 つまり、有望そうなアイデアがあるだけでは十分ではないのです。 ディープラーニングがこれらの昔のアイデアよりも遥かに強力であることをどう証明するのでしょうか? アイデアがどれほど強力で有望かを定量化する方法はあるのでしょうか? そこでコンウェイの法則の出番です。 コンウェイの法則では、雑でヒューリスティックな近似指標として、アイデアに関係する社会構造の複雑さを評価することを提案しています。
さあ、2つの質問を考えましょう。 1つ目は、ディープラーニングに関連するアイデアはどれほど強力なのかについてです。 これは、社会的複雑性の指標で評価します。 2つ目は汎用人工知能を実現するために、どれほど強力な理論が必要なのかについてです。
一つ目の質問についてまず考えます。 今日のディープラーニングを眺めると、興味深くて進展も速いですが、比較的一枚岩の分野ではあります。 幾つかの深いアイデアがあり、幾つかの会議があり、それらの会議は実質的な重なりがあります。 そして、どの論文も同じ基礎的なアイデアを使っています。 どの論文でも、確率的勾配降下法(かその変種)を用いて、コスト関数を最適化しています。 それらのアイデアが上手くいくのは素晴らしいことです。 しかし、深いアイデアをそれぞれ探索し、ディープラーニングを各方向へ押し広げるような、学問分野の下位部分はまだないようです。 したがって社会的複雑さの指標に従って、誤解を恐れずに言えば、ディープラーニングはまだまだ浅い分野であると断言できます。 まだ一人の人間が、全ての深いアイデアを習得することが可能な分野なのです。
今度は二つ目の質問に取り組みます。 AIに到達するには、どれだけの複雑さと強力さを備えたアイデアが必要なのでしょうか? もちろん、この質問への答えは誰にも分かりません。 しかし、付録では、この質問に対する実験を行っています。 どれだけ楽観的に言ったとしても、AIを作るには深いアイデアがとてもたくさん必要です。 そしてそこに到達するには、そのような深い洞察を反映するような、複雑で驚くべき社会的構造が現れる必要があることをコンウェイの法則が示唆しています。 ニューラルネットワークとディープラーニングには、このような複雑な社会構造はまだありません。 したがって、ディープラーニングを使って汎用AIを開発するのには、まだ数十年かかるはずです。
ここまで、暫定的な議論を構築するのに苦労しました。 この議論の流れは明らかであるように見えるものの、結論はぼんやりとしています。 きっと、厳密さを追い求める人々をイライラさせていると思います。 オンラインの文献を読んでいると、とても確信をもって主張をしている人が、AIに対して強い意見をもっているのに、 実はその論理が薄っぺらいものであったり、存在しない証拠に依存していたりするのをよく見ます。 私の率直な意見として、時期尚早で何も言うことはありません。 次のような古いジョークがあります。 科学者に発見はどれだけ先かを尋ねると、「10年(以上)」と答えます。 その意図は「私にはいい考えがない」というものです。 AIは、制御核融合や他の技術のように、10年プラス60年以上、その実現には時間がかかるでしょう。 反面、ディープラーニングの能力は非常に強力で、その限界は今のところ分かっていません。 そして、本質的な問題もまだまだたくさんあります。 これはとてもクリエイティブで夢のある話だと思いませんか。






