ニューラルネットワークと深層学習

What this book is about

On the exercises and problems

ニューラルネットワークを用いた手書き文字認識

• Perceptrons
• Sigmoid neurons
• The architecture of neural networks
• A simple network to classify handwritten digits
• Learning with gradient descent
• Implementing our network to classify digits
• Toward deep learning

逆伝播の仕組み

• Warm up: a fast matrix-based approach to computing the output from a neural network
• The two assumptions we need about the cost function
• The Hadamard product, $s \odot t$
• The four fundamental equations behind backpropagation
• Proof of the four fundamental equations (optional)
• The backpropagation algorithm
• The code for backpropagation
• In what sense is backpropagation a fast algorithm?
• Backpropagation: the big picture

ニューラルネットワークの学習の改善

• The cross-entropy cost function
• Overfitting and regularization
• Weight initialization
• Handwriting recognition revisited: the code
• How to choose a neural network's hyper-parameters?
• Other techniques

ニューラルネットワークが任意の関数を表現できることの視覚的証明

• Two caveats
• Universality with one input and one output
• Many input variables
• Extension beyond sigmoid neurons
• Fixing up the step functions
• Conclusion

ニューラルネットワークを訓練するのはなぜ難しいのか

• The vanishing gradient problem
• What's causing the vanishing gradient problem? Unstable gradients in deep neural nets
• Unstable gradients in more complex networks
• Other obstacles to deep learning

深層学習

• Introducing convolutional networks
• Convolutional neural networks in practice
• The code for our convolutional networks
• Recent progress in image recognition
• Other approaches to deep neural nets
• On the future of neural networks

Appendix: 知性のある シンプルな アルゴリズムはあるか?

Acknowledgements

Frequently Asked Questions

---

Sponsors

著者と共にこの本を作り出してくださったサポーターの皆様に感謝いたします。 また、バグ発見者の殿堂に名を連ねる皆様にも感謝いたします。 また、日本語版の出版にあたっては、翻訳者の皆様に深く感謝いたします。

この本は目下のところベータ版で、開発続行中です。 エラーレポートは mn@michaelnielsen.org まで、日本語版に関する質問は muranushi@gmail.com までお送りください。 その他の質問については、まずはFAQをごらんください。

---

Resources

Code repository

Mailing list for book announcements

Michael Nielsen's project announcement mailing list

---

著：Michael Nielsen / 2014年9月-12月
訳：「ニューラルネットワークと深層学習」翻訳プロジェクト

最初にゴルフを始めようとするとき、まずは基本スイングの練習にほとんどの時間を使うのが普通です。それ以外のスイングの練習をするのは、少しずつしかできません。チップやドローやフェードを身につけるのは、基本スイングの上に、修正しながら組み立てるものです。 同様に、私達はいままで逆伝搬法に集中してきました。それが私達にとっての「基本スイング」であり、ニューラルネットワークにおけるほとんどの仕事を理解するための基本だったからです。この章では、純粋な逆伝搬の実装を改善しネットワークの学習のしかたを改善するいくつかのテクニックを説明します。

この章で説明するテクニックは以下のとおりです。クロスエントロピーと呼ばれるより良いコスト関数、 ネットワークを学習データによらず汎化するのに役立つ「正規化」法と呼ばれる4つの手法（L1正規化およびL2正規化、ドロップアウト、そして人工的な学習データの伸張）、 ネットワークの中の重みを初期化するより良い方法、 そして、ネットワークに対して良いハイパーパラメータを選択するためのいくつかの発見的方法です。また、それ以外のいくつかのテクニックについても、あまり細部にこだわらず概観します。 これらの議論は完全にお互いに独立なので、必要に応じて読み飛ばすこともできます。また、多くのテクニックを動くコードとして実装もします。それらの実装を使うと、第1章で説明した手書き文字の分類問題の結果が改善されます。

もちろん、ここではニューラルネットワークのために開発されたとても多くの手法のうちほんの少しを紹介するだけです。ここでの哲学は、利用できる手法が沢山ありすぎる場合の最も良い入門は、少しの手法を深く学習することだということです。それらの重要な手法はそのまま役に立つというだけではなく、ニューラルネットワークを使うときに起こる問題に対する理解を深めてくれます。その結果、必要に応じて他のテクニックを即座に使えるようになるでしょう。

クロスエントロピーコスト関数

ほとんどの人にとって、間違えることは嫌なことです。私はピアノを習い始めてすぐに聴衆の前で演奏することがありました。そのとき緊張していたので、1オクターブ低く演奏を始めてしまいました。私は混乱してしまい誰かが間違いを指摘するまで気づきませんでした。とても恥ずかしい思いをしました。私達は、はっきり間違えているときには、嫌な思いをしつつも速く学ぶことができます。次に私がピアノを聴衆の前で弾くときには正しいオクターブで弾いたということは、いうまでもないでしょう。一方で、間違いがはっきりしないときはゆっくりとしか学べません。

理想的にはニューラルネットワークは間違いから学んでほしいと、我々は願っていて期待もしています。そのようなことは実際に起こるでしょうか。この問いに答えるために簡単な例を見てみましょう。この例はちょうど一個の入力を持つニューロンです。

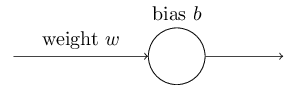
バカバカしいほど簡単なことをするためにこのニューロンを学習させます。入力1に対して出力0を返すようにします。もちろんこれは適当な重みとバイアスをすぐに手計算でき、学習アルゴリズムを使わないですむような自明な作業です。しかし、最急降下法を使って重みとバイアスを計算することは理解に役立ちます。ですから、ニューロンがどのように学ぶかを見てみましょう。

話をはっきりするために、初期の重みを$0.6$、バイアスを$0.9$としましょう。この設定は学習の前の設定として適当に選んだもので、とにかく特別な値を採用したわけではありません。ニューロンからの出力の初期値は$0.82$なので、ニューロンが望まれる出力の$0.0$を出すようになるようになるには、それなりの時間がかかりそうです。出力が$0.0$にとても近くなるまでにどのようにニューロンが学習していくかを見るには、右下にある「Run」ボタンを押してみてください。これは録画された動画ではないことに注意してください。ブラウザは実際に勾配を計算して、その勾配は重みとバイアスを更新するのに使われて、結果が表示されています。学習係数は$\eta = 0.15$であり、これの値は、なにが起こっているかを見るには十分に遅く、しかし数秒でそれなりの学習をさせるには十分に速い値です。コスト関数は、第1章で紹介した二次コスト関数です。コスト関数の厳密な式は後で復習するので、今とくに定義を深く追う必要はありません。このアニメーションは「Run」を押せば何度でも実行できます。

これでわかるように、ニューロンは急速に重みとバイアスを学習していき、コストを下げていきます。結果としてニューロンからの出力は$0.09$になります。これは望まれる出力$0.0$とは違いますが、良い値です。しかしながら、最初の重みとバイアスとして$2.0$という値を選んだとしてみましょう。この場合にニューロンがどのように出力が$0$になるように学習していくかを見てみましょう。今度も「Run」を押してください。

この例は同じ学習係数($\eta = 0.15$)を使っているのにもかかわらず、学習がずっとゆっくり始まることがわかります。実施、最初の150エポックくらいでは重みやバイアスはほとんど変わりません。その後に学習が始まり、最初の例と同じように出力は急速に$0.0$に近づきます。

この振る舞いは人間の学習と比べると奇異に見えます。この節の最初に言ったように、我々はひどく間違った時に速く学習することが多いです。ですが、我々の人工的なニューロンは、ひどく間違っている時のほうが、少しだけ間違えていた時と比べて学習がとても困難であったように見えます。さらにいうと、このような振る舞いはこの単純なモデルだけに起こることではなく、もっと一般的なネットワークでも起こることがわかっています。なぜ学習がそんなに遅いのでしょう？そして、このように遅くなることを防ぐ手段はあるのでしょうか？

問題の原点を理解するために我々のニューロンが、重みとバイアスをコスト関数の偏微分$\partial C/\partial w$と$\partial C / \partial b$によって決まる値で更新されるとしましょう。「学習が遅い」ということは、その偏微分が小さいということと同じことです。問題は、なぜこれが小さいのかということを理解することです。そのことを理解するために偏微分を計算してみましょう。我々は二次導関数を使っていたことを思い出しましょう。これは、式(6)\begin{eqnarray} C(w,b) \equiv \frac{1}{2n} \sum_x \| y(x) - a\|^2 \nonumber\end{eqnarray}から、次の式で与えられます。 \begin{eqnarray} C = \frac{(y-a)^2}{2}, \tag{54}\end{eqnarray} ここで、$a$は学習の入力$x = 1$に対するニューロンの出力であり、$y = 0$は対応する期待される出力です。このことを重みとバイアスの言葉でもっとはっきり記述するために、$z = wx+b$のとき$a = \sigma(z)$と表せることを思い出しましょう。合成関数微分の公式を使い、重みとバイアスで微分すると以下の式を得ます。 \begin{eqnarray} \frac{\partial C}{\partial w} & = & (a-y)\sigma'(z) x = a \sigma'(z) \tag{55}\\ \frac{\partial C}{\partial b} & = & (a-y)\sigma'(z) = a \sigma'(z), \tag{56}\end{eqnarray} ここで、$x = 1$と$y = 0$の代入を使いました。これらの表現の振る舞いを理解するためには、右辺に出てくる$\sigma'(z)$の項に注目しましょう。関数$\sigma$のグラフの形状をみてみましょう。

クロスエントロピーコスト関数の導入

学習が遅くなる問題はどう扱えばよいでしょう。二次コスト関数のかわりに、クロスエントロピーと呼ばれる他のコスト関数を使うことで解くことができることがわかります。クロスエントロピーを理解するには、我々の非常に簡単な例からちょっとだけ離れる必要があります。その代わり、ニューロンをいつくかの入力変数$x_1, x_2, \ldots$で学習させることとし、それらのそれぞれに対応する重みを$w_1, w_2, \ldots$をとし、バイアスを$b$とします。

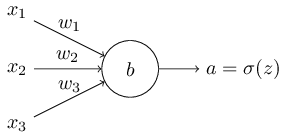
この式(57)\begin{eqnarray} C = -\frac{1}{n} \sum_x \left[y \ln a + (1-y ) \ln (1-a) \right] \nonumber\end{eqnarray}が、学習が遅くなる問題を解決するということは明らかではありません。それどころか、これをコスト関数と呼んでいいかすら明らかではないでしょう。学習が遅くなる問題に注目する前に、どういう意味でクロスエントロピーがコスト関数として解釈できるかを見てみましょう。

二つの性質によりクロスエントロピーはコスト関数であると解釈できます。一つにはそれは非負、つまり$C>0$であることです。このことを知るには、式(57)\begin{eqnarray} C = -\frac{1}{n} \sum_x \left[y \ln a + (1-y ) \ln (1-a) \right] \nonumber\end{eqnarray}のすべての項が正であることを確認すればいいです。これは、(a)両方のlogの引数が0から1の範囲なのでその値は負になり、(b)前にマイナス符号が付いているからです。

二つ目には、すべての学習の入力$x$についてニューロンの出力が望まれる出力、つまり$y=y(x)$に近いのなら、クロスエントロピーはゼロに近づく *このことそ証明するには、望まれる出力$y(x)$が$0$か$1$であることを仮定しなければなりません。これは、例えば分類問題や真偽値関数を計算しているときについては通常成り立ちます。この仮定をおかない時になにが起こるかを理解するには、この節の最後の演習を参照してください。ということです。このことを見るために、例えば同じ入力$x$に対し$y(x)=0$かつ$a \approx 0$と仮定しましょう。これはニューロンがその入力に対して良い仕事をした場合です。$y(x) = 0$なので、式(57)\begin{eqnarray} C = -\frac{1}{n} \sum_x \left[y \ln a + (1-y ) \ln (1-a) \right] \nonumber\end{eqnarray}の最初の項が消え、2項目は$-\ln (1-a) \approx 0$となります。$y(x) = 1$かつ$a \approx 1$の場合も同様な解析ができます。このことにより、実際の出力が望まれる出力に近いとき、コストへの寄与は小さいことがわかります。

まとめると、クロスエントロピーは正で、すべての学習の入力$x$と望まれる出力$y$に関して、ニューロンがより良くなるとクロスエントロピーは$0$に近づきます。この両方の性質は、私達がコスト関数に対して直感的に期待する性質です。実際、これらの性質は二次コスト関数でも満たされています。これはクロスエントロピーにとって良いニュースです。しかし、クロスエントロピーは二次コスト関数と違って、学習が遅くなる問題がないという良い性質があります。このことを見るために、クロスエントロピーの重みについての偏微分を計算してみましょう。式(57)\begin{eqnarray} C = -\frac{1}{n} \sum_x \left[y \ln a + (1-y ) \ln (1-a) \right] \nonumber\end{eqnarray}に$a = \sigma(z)$を代入して、合成関数の公式を2度適用すると以下の式を得ます： \begin{eqnarray} \frac{\partial C}{\partial w_j} & = & -\frac{1}{n} \sum_x \left( \frac{y }{\sigma(z)} -\frac{(1-y)}{1-\sigma(z)} \right) \frac{\partial \sigma}{\partial w_j} \tag{58}\\ & = & -\frac{1}{n} \sum_x \left( \frac{y}{\sigma(z)} -\frac{(1-y)}{1-\sigma(z)} \right)\sigma'(z) x_j. \tag{59}\end{eqnarray} すべてを共通の分母でまとめて簡単にすると次の式を得ます： \begin{eqnarray} \frac{\partial C}{\partial w_j} & = & \frac{1}{n} \sum_x \frac{\sigma'(z) x_j}{\sigma(z) (1-\sigma(z))} (\sigma(z)-y). \tag{60}\end{eqnarray} シグモイド関数の定義を使うと$\sigma(z) = 1/(1+e^{-z})$であり、すこしの代数的計算をすると$\sigma'(z) = \sigma(z)(1-\sigma(z))$であることがわかります。このことは演習で確認しますが、とりあえずはそれはわかっているものとして受け入れましょう。ちょうど上の式で、$\sigma'(z) = \sigma(z)(1-\sigma(z))$が消え、単純になり次のようになります： \begin{eqnarray} \frac{\partial C}{\partial w_j} = \frac{1}{n} \sum_x x_j(\sigma(z)-y). \tag{61}\end{eqnarray} これは美しい表現です。これを見ると、重みが学習する度合いは$\sigma(z)-y$つまり出力における誤りによってコントロールされてることがわかります。つまり誤りが大きくなればなるほどニューロンの学習は速くなります。これはちょうど我々が直感的に望んでいたことです。特に、二次コスト関数の同じような式、つまり式(55)\begin{eqnarray} \frac{\partial C}{\partial w} & = & (a-y)\sigma'(z) x = a \sigma'(z) \nonumber\end{eqnarray} で$\sigma'(z)$が学習の速度低下の原因となっていたがそれを防いだのです。クロスエントロピーを使うと、$\sigma'(z)$の項が消え、そこのことを心配する必要がなくなるのです。この項の消滅はクロスエントロピーで起こる特別な奇跡です。実際には奇跡ではありません。あとでわかるように、クロスエントロピーはこの性質を持つように特別に選ばれたのです。

同じようにバイアスについての偏微分も計算します。また詳細を追うことをしませんが、次の式が確認できます。 \begin{eqnarray} \frac{\partial C}{\partial b} = \frac{1}{n} \sum_x (\sigma(z)-y). \tag{62}\end{eqnarray} 繰り返しますが、これにより二次コストの同じような式、つまり式(56)\begin{eqnarray} \frac{\partial C}{\partial b} & = & (a-y)\sigma'(z) = a \sigma'(z) \nonumber\end{eqnarray} で$\sigma'(z)$が学習速度低下の原因になるのを防いでいます。

演習

• $\sigma'(z) = \sigma(z)(1-\sigma(z))$であることを確認しなさい

前に遊んでみたおもちゃのような例にもどり、二次コスト関数の代わりにクロスエントロピーを使うとどうなるか見てみましょう。方向転換して、まずは二次コスト関数がうまく行くケースとして、重みが$0.6$、バイアスが$0.9$のときから始めましょう。

驚くまでもなく、この例では前と同じようにニューロンは完璧に学習します。では今度は、以前にニューロンが停滞したケース(link, for comparison)、つまり重みとバイアスが両方とも$2.0$から始めるケースを見てみましょう：

うまくいきました！今度はニューロンは望んだ通り早く学習します。近づいて見ると、コスト曲線の坂は、二次コスト関数の対応する初期値の平らな部分と比べると、もっと急になっていることがわかります。その傾きはクロスエントロピーがうまくやってくれていて、ニューロンが最も速く学習してほしい時に停滞してしまうこと、つまりニューロンが間違った起動のしかたをすることを防いでくれます。

例で使われた学習率とはなにかについていってませんでした。以前、二次コスト関数では$\eta = 0.15$を使っていました。同じ例でも同じ学習率を使うべきでしょうか？ところが、コスト関数を変更してしまうと、学習率が「同じ」とはどういうことかを正確には言えません。リンゴとオレンジを比べているようなものです。両方のコスト関数に対して、なにが起こっているかわかるような学習率を、単純に私は経験的に見つけていたというだけです。

そんなことではグラフに意味がないではないかと、あなたは反対するかもしれません。学習率の選択法が決まっていないのに、ニューロンの学習する速さに誰が興味を持つだろうか！？そのような反対意見は重要な点を見逃しています。グラフで重要な点は学習の絶対的な速度についてではないのです。学習の速度がどのように変わっていくかが重要なのです。取り立てて言うと、二次コスト関数は、後に正しい出力値に近づいたときと比べて、ニューロンがあきらかに間違っている状態の時に遅いのです。一方で、クロスエントロピーは、あきらかに間違っている状態の時にも速いです。これらの話は学習率がどのように設定されたかに依存しません。

私達は、一つのニューロンのときのクロスエントロピーを調べてきました。しかし、多層の多くのニューロンの場合に汎化するのは簡単です。とくに、$y = y_1, y_2, \ldots$がニューロンの望まれる出力だと仮定しましょう。つまり、ニューロンの最終層の出力です。また、$a^L_1, a^L_2, \ldots$がニューロンの実際の出力だとしましょう。ここで、クロスエントロピーを次の式で定義します。 \begin{eqnarray} C = -\frac{1}{n} \sum_x \sum_j \left[y_j \ln a^L_j + (1-y_j) \ln (1-a^L_j) \right]. \tag{63}\end{eqnarray} これは以前の表現、式(57)\begin{eqnarray} C = -\frac{1}{n} \sum_x \left[y \ln a + (1-y ) \ln (1-a) \right] \nonumber\end{eqnarray}と比べて、すべてのニューロンについての和$\sum_j$をとったことをのぞいて同じです。微分を明示的に計算することはしませんが、式(63)\begin{eqnarray} C = -\frac{1}{n} \sum_x \sum_j \left[y_j \ln a^L_j + (1-y_j) \ln (1-a^L_j) \right] \nonumber\end{eqnarray}を使えば多くのニューロンのネットワークで学習の速度低下を防げることはすばらしいことでしょう。もし興味があれば、後述する問題で微分を計算してみることはできます。

二次コスト関数の代わりにクロスエントロピーを使うべきなのはいつでしょうか？ところが、出力ニューロンがシグモイドニューロンであるときには、クロスエントロピーはほとんどいつもよりよい選択なのです。なぜかを理解するためには、ニューロンを設定するときには、通常重みとバイアスを同じ種類の乱数で初期化するということを考慮しなければいけません。そのような初期値は、学習の入力により決定的に悪くなる可能性があります。つまり、出力ニューロンが$0$であるべき場合に$1$付近で止まってしまったり、その逆もあり得るということです。二次コスト関数を使っていたとしたら、学習は遅くなります。重みは他の入力から学ぶことを続けるので、学習が完全に停止することはありませんが、それは明らかに私達が望んでいないことです。

演習

• クロスエントロピーについて気をつけなければいけないのは、最初は$y$と$a$のそれぞれの役割を覚えるのが難しいところです。正しい式が$-[y \ln a + (1-y) \ln (1-a)]$であったか、$-[a \ln y + (1-a) \ln (1-y)]$であったかという点はよく混乱します。これらの後者の式の方で$y=0$または$y=1$だった場合なにが起こるでしょう？このことは前者の式に悪影響があるでしょうか？理由を考えてください。

• この節の最初の一つのニューロンでの考察で、もし学習データの入力で$\sigma(z) \approx y$ならばクロスエントロピーは小さくなるという議論をしました。この議論は$y$は$0$または$1$であるという仮定の元にでした。この仮定は分類問題では通常は正しいですが、他の問題（例えば回帰問題）では$y$はときに$0$から$1$の間の値をとることがあります。すべての学習の入力について、クロスエントロピーは$\sigma(z) = y$で最小になることを示してください。これが成り立つときクロスエントロピーは次の値をとります： \begin{eqnarray} C = -\frac{1}{n} \sum_x [y \ln y+(1-y) \ln(1-y)]. \tag{64}\end{eqnarray} 値$-[y \ln y+(1-y)\ln(1-y)]$は バイナリエントロピーと呼ばれることもあります。

問題

• 多層複数ニューロンのネットワーク 前章で導入した記法を使って、出力層で二次コスト関数の重みについての微分は次の式になることを示しなさい： \begin{eqnarray} \frac{\partial C}{\partial w^L_{jk}} & = & \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \sigma'(z^L_j). \tag{65}\end{eqnarray} ここで$\sigma'(z^L_j)$の項は、出力ニューロンが悪い値で停滞した時に学習の速度低下を引き起こします。クロスエントロピーについて、一つの学習データの例$x$についての出力誤差$\delta^L$の重みは次の式で表されることを示しなさい： \begin{eqnarray} \delta^L = a^L-y. \tag{66}\end{eqnarray} この式を使って、出力層の重みについての偏微分は次の式で与えられることを示しなさい： \begin{eqnarray} \frac{\partial C}{\partial w^L_{jk}} & = & \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j). \tag{67}\end{eqnarray} $\sigma'(z^L_j)$の項が消え、ニューロンが一つでなく多層複数ニューロンの場合でも、クロスエントロピーは学習の速度低下を避けることがわかりました。この解析の簡単な変形でバイアスについても同じことがいえます。もしそれが明らかではないなら、同様の解析を続けてやるべきです。

• 出力に線形ニューロンがあるときの二次コストの使用 多層複数ニューロンのネットワークがあるとします。最終層のニューロンはすべて線形ニューロンであると仮定します。線形ニューロンとは、シグモイド関数が適用されず、出力が単純に$a^L_j = z^L_j$であることを意味します。二次コスト関数を使えば、一つの学習データの例$x$に対する出力誤差$\delta^L$は次の式で与えられることを示しなさい： \begin{eqnarray} \delta^L = a^L-y. \tag{68}\end{eqnarray} 前の問題と同様に、この式を使うと、出力層での重みとバイアスについての偏微分は次の式で与えられることを示しなさい： \begin{eqnarray} \frac{\partial C}{\partial w^L_{jk}} & = & \frac{1}{n} \sum_x a^{L-1}_k (a^L_j-y_j) \tag{69}\\ \frac{\partial C}{\partial b^L_{j}} & = & \frac{1}{n} \sum_x (a^L_j-y_j). \tag{70}\end{eqnarray} このことにより、もし出力ニューロンが線形ニューロンならば、二次コスト関数は学習の速度低下について何の問題も産まないことがわかります。このケースでは、二次コスト関数はそれどころか使うべき適切なコスト関数です。

クロスエントロピーを使ったMNISTの分類

最急降下法とバックプロパゲーションを使って学習プログラムの一部として、クロスエントロピーを実装するのは簡単です。そのことはこの章のあとで、MNISTの手書き数字の分類に関する前述のプログラムnetwork.pyの改善版を開発することで示します。 新しいプログラムはnetwork2.pyという名前で、これはだたクロスエントロピーを取り込んだだけではなく、この章で使ったいくつかのテクニックを取り込んでいます* *コードはGitHub上から手に入れることができます。。 ここで、私達の新しいプログラムがどのくらいうまくMNISTの数字を分類するかを見てみましょう。第1章と同様に、$30$個の隠れニューロンを持つネットワークを使い、ミニバッチサイズとして$10$を使います。学習率を$\eta = 0.5$* *1章では二次コスト関数を使い、学習率$\eta = 3.0$としました。前の議論により、コスト関数が違うときに「同じ」学習率を使うというのはどういうことか、正確に言うことはできません。両方のコスト関数について、私は実験をして、与えられたハイパーパラメータに対してほぼ最適なパフォーマンスを出す学習率を見つけました。

クロスエントロピーと二次コストの学習率については、非常に大雑把な一般的な発見的手法が存在します。前に見たように、二次コストの勾配項の中には、$\sigma' = \sigma(1-\sigma)$という余計な項があります。この値を$\sigma$について平均をとってみると、$\int_0^1 d\sigma \sigma(1-\sigma) = 1/6$となります。これにより、（非常に大雑把にいうと）二次コストは同じ学習率について、平均すると$6$倍遅く学習するということがわかります。このことは、妥当な出発点は二次コストの学習率を$6$で割ることだということを示唆しています。もちろん、この議論は厳密からは程遠いですし、あまり真剣にとらえるべきではないです。とはいえ、それは時には役に立つ出発点となります。とし、$30$エポック学習させます。 network2.pyのインターフェースはnetwork.pyと少し違いますが、何が起こっているかはわかると思います。ところで、network2.pyのインターフェースに関するドキュメントは、Pythonのシェルからhelp(network2.Network.SGD)と入力することで見ることができます。

>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data, 30, 10, 0.5, evaluation_data=test_data,
... monitor_evaluation_accuracy=True)

ここで注意ですがnet.large_weight_initializer()コマンドは第1章で示したのと同じように重みとバイアスを初期化します。このコマンドを実行しなければいけないのは、この章で後ほど、ネットワークの重みのデフォルト初期値を変更するからです。上記のコマンド列を実行した結果は$95.49$％の的中率になります。これは1章で二次コストによって得られた的中率$95.49$％にとても近いです。

$100$個の隠れニューロンを使い、クロスエントロピーを使いそれ以外のパラメータは同じにしたケースを見てみましょう。この場合、的中率は$96.82$％になります。これは二次コストを使って的中率$96.59$であった1章の結果からすると大きな改善です。これは小さな変化に見えるかもしれませんが、誤り率は$.41$％から$3.18$％に下がっています。これは元の誤り14個につき1個を消したということです。これはとてもありがたい改善です。

クロスエントロピーコストは二次コストと比べて同等かより良い結果をもたらすと言いたくなるかもしれません。しかし、これらの結果はクロスエントロピーがより良い選択であることを証明したと結論付けるわけにはいかないのです。なぜなら、学習率やミニバッチサイズのようなハイパーパラメータの選定にまだ十分な努力をしていないからです。この改善に本当に説得力を持たせるには、そのようなハイパーパラメータを徹底的に最適化しなければいけません。とはいってもここまでの結果は、クロスエントロピーは二次コストよりよいのではという前述の議論を後押し補強するものです。

ところでこれは、この章を通して見られる一般的なパターンであり、さらにはこの本の残りを通しても見られるパターンです。我々は新しいテクニックを展開し、それを試し、そして「改善した」結果を得るということを行います。もちろんそのような改善はよいことです。しかし、その改善の解釈はいつも問題があります。他のハイパーパラメータの最適化に莫大な努力をして改善が見られるときに、初めてそれらのテクニックは真の説得力を持ちます。それは大変な量の仕事で、多くの計算資源を必要とするので、通常はそのような網羅的な調査は行いません。そのかわり、いままでやってきたように非形式的なテストを行います。一方で、そのようなテストは絶対的な証明としては不十分だということを忘れず、議論が崩壊しそうな兆候には警戒し続けてください。

ここまでクロスエントロピーについて長い間議論してきました。MNISTの結果にほんの少しの改善をするだけなのに、なぜそんなに労力をつかうのでしょう? この章の後で他のテクニック、特に正規化などを見ますが、それらはもっと大きな改善をします。ならばどうしてクロスエントロピーにそんなに力をいれるのでしょう? 理由の一つは、クロスエントロピーは広く使われているコスト関数でなので、よく理解する価値があるからです。しかしもっと大事な理由は、ニューロンの飽和がニューラルネットで重要な問題で、その問題はこの本を通して繰り返し触れることだからです。そのため、私はクロスエントロピーについて長く議論してきましたが、それはニューロンの飽和を理解し、どのように処理されるべきかを理解するために良い実験室であったのでした。

クロスエントロピーは何を意味するのか? それはどこから来たのか?

クロスエントロピーについての私達の議論は、代数的な分析と実用的な実装に集中してきました。それは役に立ちますが、もっと大きな思想的な問題が解かれていません。例えば、クロスエントロピーは何を意味するのか? クロスエントロピーを直感的に考える方法があるだろうか? どうやったらクロスエントロピーのようなものを最初に思いつくのか? といったことです。

ここでの定数はそれぞれの学習データのサンプルに対する定数の平均値です。 式(71)\begin{eqnarray} \frac{\partial C}{\partial w_j} & = & x_j(a-y) \nonumber\end{eqnarray}と(72)\begin{eqnarray} \frac{\partial C}{\partial b } & = & (a-y) \nonumber\end{eqnarray}により、クロスエントロピーの式を定数項を除いて唯一に定めます。クロスエントロピーは薄い空気の中から奇跡的に生まれるものではないのです。むしろ単純かつ自然に発見されるべきものなのです。

クロスエントロピーの直感的な意味はなんでしょうか? どうやったらそのようなことを考えられるのでしょう? このことを深く説明するのは、行きたいところよりさらに遠くに連れて行かれてしまうかもしれません。しかしクロスエントロピーは情報理論から来ているのですが、それを解釈する標準的方法があるということに触れておくことは価値があるでしょう。大雑把にいうと、クロスエントロピーとは驚きの尺度です。特に私達のニューロンは関数$x \rightarrow y = y(x)$を計算しようとしています。しかしそのかわり関数$x \rightarrow a = a(x)$を計算しようとしています。ここで$a$はニューロンが計算した$y$が$1$である確率だとして、同じように$1-a$は計算された$y$が$0$である確率だとしましょう。そうすると、クロスエントロピーは真の$y$の値を学習するときに平均的にどのくらい「驚き」を得るかを示します。出力が期待したどおりだとあまり驚かないし、期待していないものだと強く驚きます。もちろん私は「驚き」を正確に説明していないので、これは中身のないおしゃべりに見えるかもしれません。しかし実際に、驚きが何を意味するかを説明する、正確な情報理論的手法があるのです。これについて、良い、短い、自己完結したオンラインで入手可能な議論を私は見たことがないです。でももしこれについて掘り下げたいのなら、ウィキペディアは簡単なまとめがあり、これにより正しい方向に向かうことができるでしょう。情報理論についての本「Cover and Thomas」の5章に書かれているKraft不等式についての説明をあたってみれば、さらに詳細を埋めることができるでしょう。

問題

• 学習に二次コストを使ったネットワークで出力ニューロンが飽和したときに学習の速度低下が起こることを時間をかけて議論してきました。学習を抑制する他の因子は、式(61)\begin{eqnarray} \frac{\partial C}{\partial w_j} = \frac{1}{n} \sum_x x_j(\sigma(z)-y) \nonumber\end{eqnarray}の$x_j$の項の存在です。この項により、入力$x_j$がゼロに近ければ対応する重み$w_j$の学習は遅くなります。賢いコスト関数を選んでも、この$x_j$の項を消すのは不可能であることを説明してください。

過適合と正規化

ノーベル賞受賞者の物理学者エンリコ・フェルミはあるとき、 とある物理の未解決問題の解としてあるグループが提案した数学的モデルについての意見を求められました。 そのモデルは実験と非常に良い一致をみせていましたが フェルミは懐疑的でした。 フェルミは、そのモデルには自由に設定できるパラメータがいくつあるか、と尋ねました。 答えは４つ、ということでした。 そこでフェルミはこう答えたそうです。 *このエピソードは、 フリーマン・ダイソン のチャーミングな文章から引用したものです。ダイソンはまさにフェルミが批判したモデルの提案者の一人でした。 4パラメータの象は ここ にあります。 : 「私の友人ジョン・フォン・ノイマンが言っていたよ。私ならパラメータが4つあれば象だってフィッティングできる、5つあれば象の鼻を振れる、とね。」

この話のポイントは、もちろん、モデルの自由パラメータの数が多ければ、驚くほど多くの現象を説明できてしまう、という点です。 たとえ手元のデータと良く一致したとしても、そのようなモデルが良いモデルだとは一概には言えません。 もしかすると、そのモデルは、与えられたデータの 背後にある現象になんら本質的な洞察を与えることなく、 パラメータの多さにまかせてとりあえず フィットできてしまうだけなのかもしれません。 もしこれが起こっているなら、このモデルは既存のデータに対してはよくあてはまりますが、 新しい状況への汎化に失敗するでしょう。 モデルの真価は、そのモデルが経験したことないような状況での予言力で測られるのです。

フェルミとフォンノイマンは、4つしかパラメータのないモデルに対してすでに懐疑的でした。 30個の隠れニューロンを持つ私たちのMNIST分類ネットワークには、なんと約24,000個ものパラメータがあります！ うわっ、私のパラメータ、多すぎ？100個の隠れニューロンがあるネットワークなら、パラメータの数は8万個近くにもなり、 そして最新の深層学習ニューラルネットにはときに何百万、何億という数のパラメータが含まれます。 こんなものを信じて、大丈夫でしょうか？

この問題の具体例として、私たちのニューラルネットワークが新しい状況に適応できない状態というのを 実際に作ってみましょう。まず、使うのは隠れニューロン30個、パラメータが23,860個のモデルです。ただし、 MNISTの50,000個の画像を全部使わず、先頭1,000個の画像だけを使います。データ集合を制限することで、汎化失敗現象が見やすくなります。 訓練方法は以前と同様、学習率$\eta = 0.5$、ミニバッチサイズ$10$を採用します。ただし、訓練例が少ないぶん、訓練期間は400エポックと、以前より長くします。 コスト関数の変化のようすを見るためにnetwork2を使いましょう：

>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data[:1000], 400, 10, 0.5, evaluation_data=test_data,
... monitor_evaluation_accuracy=True, monitor_training_cost=True)

この結果を用いて、学習の進行に対するコスト関数の変化をプロットしてみます* *このグラフと、次の4つのグラフは overfitting.py から生成しています。 :

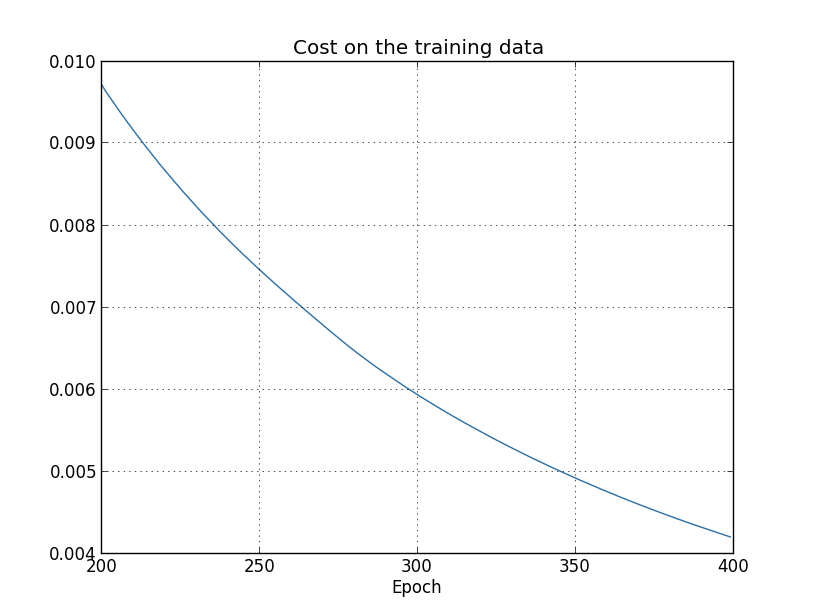
期待通り、コストはなめらかな減少を示しています。 学習後期のふるまいを拡大して観察したいので、 上図ではエポック200 - 399だけを表示しています。 この学習後期で起こっている面白い現象を、これからみていきます。

こんどは、試験データの分類精度がどう変化しているか見てみましょう：

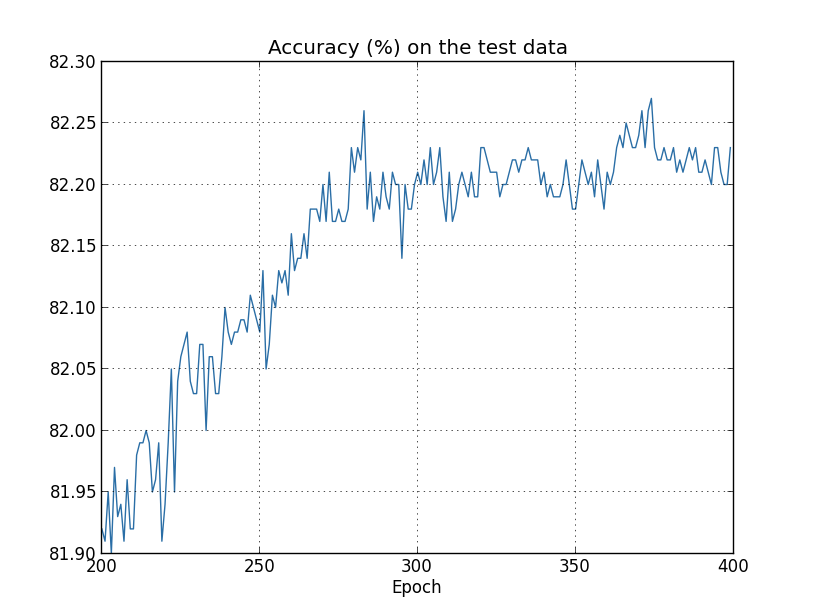
この図も、かなり拡大して見せています。図の範囲に入る以前の、最初の200エポックで 精度は82パーセント直前まで上昇しています。その後、学習はだんだん鈍化し、ついに280エポック付近で分類精度はほとんど改善がみられなくなります。 以降は、280エポックにて達成した精度のまわりに、小さな統計的ゆらぎが見られるだけになります。 このグラフと、訓練データのコスト関数がなめらかに減少しつづける以前のグラフを見比べてください。 コスト関数を見るかぎり、モデルの性能はいっけん良くなり続けているようです。しかし試験データの分類精度をみると、 コスト関数でみられた「改善」は幻であることがわかります。 エポック280以降のニューラルネットワークが学習した知識は、 フェルミがディスっていたモデルと同じく、試験データに汎化できない知識だったのです。 したがって、有用な学習ではなかった、といえます。このようなとき、エポック280以降のニューラルネットワークは 過適合している、 過学習している、などと言います。

もしかして、訓練データのコスト関数と、試験データの 分類精度という、異なるものを比較したのがいけなかったのかもしれません。 それでは、訓練データのコスト関数と試験データのコスト関数同士を較べたらどうでしょうか？ 逆に、訓練データと試験データの分類精度を比べたらどうでしょうか？実は、 どの方法で比較しても、同じような過学習の兆候が見られます。ただし、 細部には確かに違いがあります。例えば、試験データのコスト関数を見てみましょう：

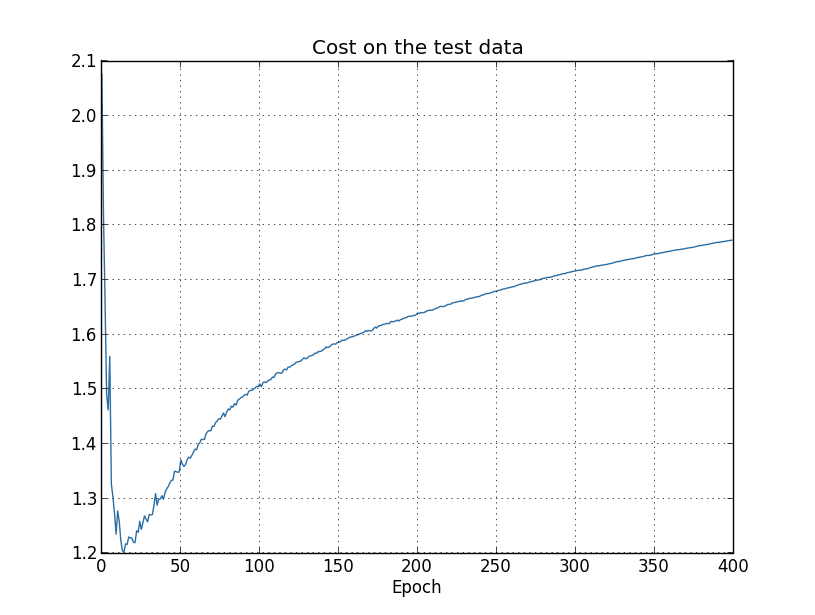
図から、試験データのコスト関数はエポック15あたりまでは改善していくが、その後は実は 悪化しはじめていたことがわかります。いっぽうで訓練データのコスト関数は改善しつづけていますから、 これもまた過適合の兆候であるといえます。もっとも、ここで1つの疑問がわいてきます。学習は どの時点から過適合に陥ったと見做すべきでしょうか？ エポック15からでしょうか、それともエポック280？ 実用的な観点からいえば、私たちの本来の目的は試験データの分類精度を向上させることであって、 試験データのコスト関数は分類精度の間接的な指標にすぎません。ですから、エポック280をもって 学習が過適合に陥った時点と見做すのが最も合理的といえます。

訓練データの分類精度にも、過学習の兆候が現れています：

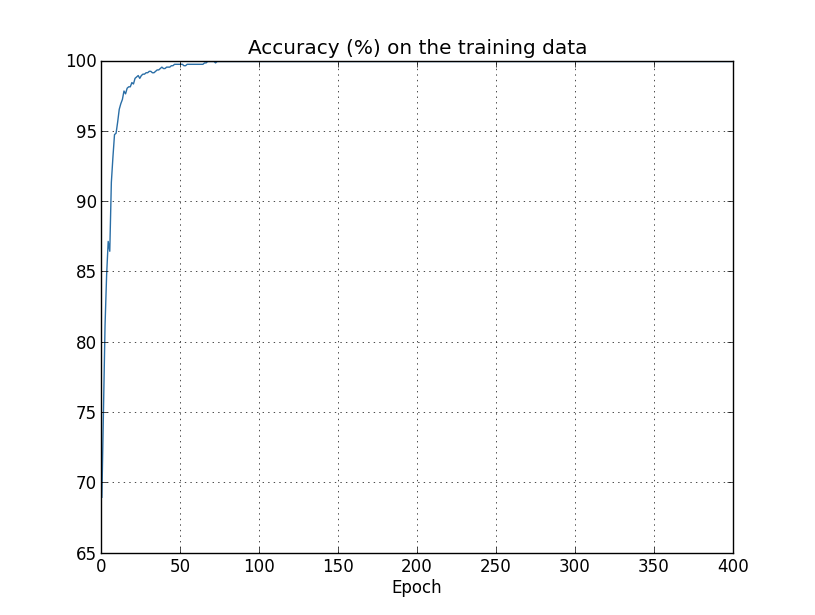
精度が100パーセントまでひたすら向上しています。つまり、私たちのニューラルネットワークは 1,000件の訓練画像をすべて正しく分類しているのです！いっぽう、試験データの分類精度は せいぜい82.27パーセント程度が最大です。つまり、私たちのニューラルネットワークはもはや 数字の認識一般を学習しているのではなく、訓練データ画像に特有の癖を学習してしまっているのです。 数字とは何かを理解し試験データにも汎化できるような理解を得ようとせずに、ただ訓練データを丸暗記してしまっている、 と言ってもよいでしょう。

過適合はニューラルネットワークの持つ大問題です。 特に、現代のニューラルネットワークはしばしば極めて多数の重みやバイアスをパラメータとして持つため、過適合の問題が顕著になります。 ニューラルネットワークを効率的に学習させるためには、過適合の進行を検知し、過学習を避ける手立てが必要です。 そして、過適合の影響を軽減するための手法が望まれます。

過適合を検知する安直な方法は、上述したアプローチ、つまり、 ニューラルネットワークを訓練しながら試験データに対する精度の変化を追跡することです。 もし訓練によって試験データに対する精度が向上しなくなったら、その時点で訓練を止めるべきです。 もちろん厳密に言えば、これを過適合の兆候であると断言することはできません。 試験データと訓練データに対する精度の改善が同時に止まっているのかもしれません。 それでも、この戦略は過適合を防ぐ手段としては有効です。

実際に、私たちはこの戦略の変種を採用します。 MNISTのデータをロードする時に、私たちは3つのデータセットをロードしていることを思い出しましょう：

>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()

過適合を防ぐために、なぜ test_data ではなく validation_data を用いるのでしょうか？ 実は、過適合を防ぐために採用したこの戦略は、より一般的な戦略の一部分なのです。 より一般的な戦略とは、訓練を続けるエポック数、学習率、最適なニューラルネットワークのアーキテクチャ等の ハイパーパラメータを評価・比較するために、validation_data を用いるというものです。 そうして得られた評価を元に、良いハイパーパラメータを見つけて定めます。 実際、これまで触れてきませんでしたが、この本でこれまでに採用してきたハイパーパラメータの一部は、 私自身がこの戦略に基づいてたどり着いたものです。(これに関する詳細は後ほど)

もちろん、この説明では全く元の質問に答えたことになっていません。 過適合を防ぐために test_data ではなく validation_data を使うのはなぜか、 という質問を、より一般的な質問、つまり、良いハイパーパラメータを見つけるために test_data ではなく validation_data を使うのはなぜか、というものに 置き換えただけなのです。 この質問への回答を理解するために思い出してほしいのは、 私たちが良いハイパーパラメータを探すときには、普通、 様々な異なる値のハイパーパラメータを試しては評価を行うだろうということです。 その際、ハイパーパラメータの評価を test_data で行ったとすると、 ハイパーパラメータが test_data に対して過適合してしまう恐れがあります。 つまり、最終的なハイパーパラメータは test_data の持つ特有の癖を学習してしまい、 ニューラルネットワークが学習した成果を他のデータセットに対して汎化することができない、 ということが起こりうるのです。 ハイパーパラメータの決定に validation_data を用いることで、 このような事態を防ぎます。 そうして望ましいハイパーパラメータが得られたところで、test_data を用いた 最終的な精度評価を行います。このような手順を踏むことで、test_data に対する 評価が一般的なデータに対してニューラルネットワークが発揮するパフォーマンスの正当な評価であると、 自信を持って結論できるのです。言い方を変えると、検証データ (validation_data) は 良いハイパーパラメータを学習するために使われるある種の訓練データ (training_data) であると 言えます。このようなアプローチは、validation_data を training_data から 除外する ("hold out") ことから、ホールドアウト法と呼ばれます。

実際問題として、ニューラルネットワークのパフォーマンスを test_data によって 評価してしまった後になってから、当初の課題に対して異なるアプローチを試してみたくなる かもしれません。その時には、ニューラルネットワークの異なるアーキテクチャを試みて、 新たに良いハイパーパラメータを探しなおすことになるでしょう。このようなことをしてしまうと、 結局 test_data に対して過適合してしまう危険は無いのでしょうか？ 私たちが結果の一般性に自信を持つためには、潜在的には無限に遡ってデータ・セットを用意する 必要があるのでしょうか？この疑問に真剣に取り組むのは、深く難しい問題です。しかし、 私たちの実用上の目的に対して必要なことではないので、ここでこの疑問について深追いすることはしません。 むしろ、training_data、validation_data、そして test_data に基づく 基本的なホールドアウト法を用いて、積極的に前進したいと思います。

ここまでで、訓練画像を1,000枚に限った時に起こる過適合を見てきました。では、訓練データが 含む50,000枚の画像全てを用いた時に何が起こるでしょうか？画像の枚数以外のパラメータはそのままに （30個の隠れニューロン、学習率 0.5、ミニ・バッチの大きさは 10）、 50,000枚の画像全てを用いて30エポックに渡り訓練してみます。 ここに示しているのは、訓練データと試験データに対する分類精度のグラフです。 ここでは、以前のグラフと今回の結果との直接的な比較を行うために、検証データではなく試験データを用いています。

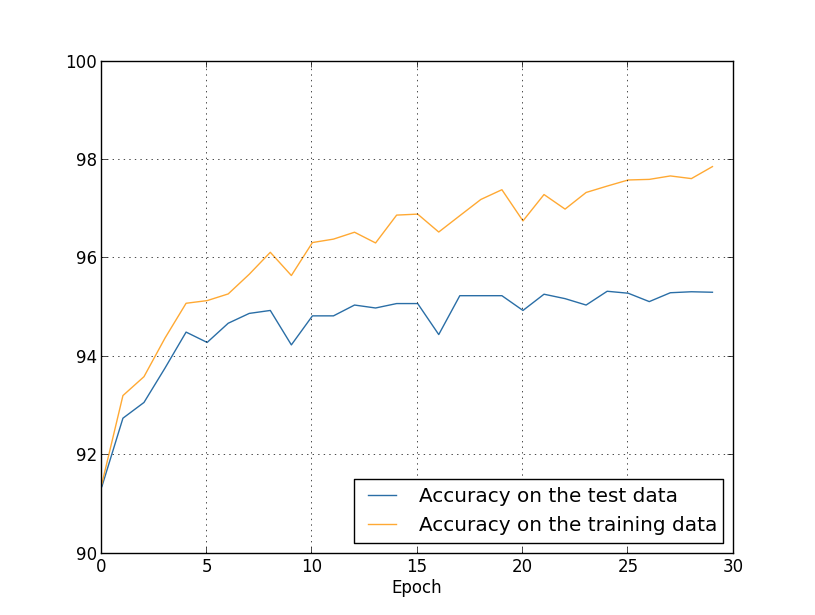
明らかに、たった1,000個の訓練例を用いた時と比べると、試験データと訓練データに対する 精度がずっと近いままでいることがわかります。訓練データに対する最大の分類精度は97.86パーセントですが、 これは試験データに対する精度 95.33パーセントと1.53パーセントしか違いません。1,000枚の訓練例に 限った時に生じた17.73パーセントのギャップを思い出してください！過適合は進行しているにしろ、 大幅に軽減されています。私たちのニューラルネットワークは、訓練データから試験データに対して、 ずっとよく汎化できています。一般的に言って、過適合を軽減する最良の方法の一つは、 より多くの訓練データを用意することです。十分な訓練データがあれば、とても大きなニューラルネットワークでさえ 過適合を起こすことはないでしょう。ただし残念ながら、 訓練データはしばしば高価だったり入手困難だったりするため、 大量の訓練データを手に入れることは常に現実的な選択肢とは限りません。

正規化

訓練データを増やすことは、過適合を軽減する一つのやり方ですが、他の方法は無いのでしょうか？ 一つの可能なアプローチは、ニューラルネットワークのサイズを小さくすることです。 しかし、大きなニューラルネットワークには小さなニューラルネットワークよりも強力な潜在能力が ありますから、これは積極的に採用するような選択肢ではありません。

幸いにも、ニューラルネットワークや訓練データの大きさを変えなくても、過適合を軽減する方法があります。 それらの手法は、正規化法として知られています。この節では、重み減衰、あるいは L2正規化として知られる手法を説明します。L2正規化は最もよく用いられる正規化手法の一つです。 L2正規化では、コスト関数に正規化項と呼ばれる余分な項を付け足します。これが、 正規化されたクロスエントロピーです：

\begin{eqnarray} C = -\frac{1}{n} \sum_{xj} \left[ y_j \ln a^L_j+(1-y_j) \ln (1-a^L_j)\right] + \frac{\lambda}{2n} \sum_w w^2. \tag{78}\end{eqnarray}

第1項はこれまで通りのクロスエントロピーの表式です。しかし今回はさらに、第2項としてニューラルネットワークの 持つ全ての重みの2乗和が足されています。この余分の項は全体に $\lambda / 2n$ の因子が掛かっています。 $\lambda > 0$ は正規化パラメータと呼ばれる実数で、$n$ はいつも通り訓練データの大きさです。 この $\lambda$ をどう選ぶかについては後ほど議論します。また、正規化項はバイアスを含まないことにも 注意しておいてください。これについても後ほど説明します。

もちろん、クロスエントロピー以外のコスト関数を正規化することも可能です。例えば、 2乗コスト関数をL2正規化すると以下のようになります：

\begin{eqnarray} C = \frac{1}{2n} \sum_x \|y-a^L\|^2 + \frac{\lambda}{2n} \sum_w w^2. \tag{79}\end{eqnarray}

どちらの場合にも、正規化されたコスト関数を次のように書けます： \begin{eqnarray} C = C_0 + \frac{\lambda}{2n} \sum_w w^2. \tag{80}\end{eqnarray} ここで、$C_0$ は元の正規化されていないコスト関数です。

直感的には、正規化することによりニューラルネットワークがより小さな重みを好むようになります。 大きな重みが許されるのは、そうすることがコスト関数の第1項を余程大きく改善する場合だけです。 言い換えると、正規化とは重みを小さくすることと元のコスト関数を小さくすることの間でバランスを取る方法であると 見ることもできます。このバランスを取る上で、2つの要素の相対的な重要性を決定するのが $\lambda$ の値です： $\lambda$ が小さい時は元のコスト関数を最小化することを好み、$\lambda$ が大きい時には より小さな重みを好むのです。

さて、実際のところ、そのようなバランスを取ることがなぜ過適合を軽減する助けになるのか、 その理由は誰の目にもすぐさま明らかなものではありません。 しかし、正規化が実際に過適合を軽減することは分かっています。 その理由については次の節で触れることにして、まずは正規化によって過適合が軽減されている例を 調べてみることにしましょう。

そのような例を作るにはまず、どうすれば正規化されたニューラルネットワークに確率的勾配降下法を 適用できるのかを明らかにする必要があります。特に、2種類の偏微分、 $\partial C / \partial w$ と $\partial C / \partial b$ をニューラルネットワークが持つ 全ての重みとバイアスに対して計算する方法を知る必要があります。 式 (80)\begin{eqnarray} C = C_0 + \frac{\lambda}{2n} \sum_w w^2 \nonumber\end{eqnarray} の偏微分を取ると、 次の表式が得られます：

\begin{eqnarray} \frac{\partial C}{\partial w} & = & \frac{\partial C_0}{\partial w} + \frac{\lambda}{n} w \tag{81}\\ \frac{\partial C}{\partial b} & = & \frac{\partial C_0}{\partial b}. \tag{82}\end{eqnarray}

偏微分項、$\partial C_0 / \partial w$ と $\partial C_0 / \partial b$ は、 前章で説明した逆伝播法を使って計算できます。 したがって、正規化されたコスト関数の勾配は簡単に計算できることがわかります。 これまで通りに逆伝播法を使って、その後に重みによる偏微分に対して $\frac{\lambda}{n} w$ を 加えれば良いのです。バイアスに関する偏微分はこれまでと何も変わりません。 つまり、バイアスに対する勾配降下法の学習規則は通常の規則そのものなのです：

\begin{eqnarray} b & \rightarrow & b -\eta \frac{\partial C_0}{\partial b}. \tag{83}\end{eqnarray}

重みに関する学習規則は次のように変わります：

\begin{eqnarray} w & \rightarrow & w-\eta \frac{\partial C_0}{\partial w}-\frac{\eta \lambda}{n} w \tag{84}\\ & = & \left(1-\frac{\eta \lambda}{n}\right) w -\eta \frac{\partial C_0}{\partial w}. \tag{85}\end{eqnarray}

これは通常の勾配降下法による学習規則とほぼ同じです。唯一の違いは、 まず最初に重み $w$ に因子 $1-\frac{\eta\lambda}{n}$ を掛けてリスケールしている点です。 この因子は重みを小さくするので、重み減衰とも呼ばれます。 一見、重みがゼロになるまでどこまでも小さくなってしまうかのように見えます。 しかし、それは正しくありません。なぜなら、他の項が正規化する前のコスト関数を小さくするために、 重みを大きくする方向に働くかもしれないからです。

これで勾配降下法のやり方は分かりました。では確率的勾配降下法は？ 実際のところ、正規化されていない確率的勾配降下法と同じことをやります。 つまり、$\partial C_0 / \partial w$ を見積もるのに、$m$個の訓練例を含むミニバッチに関して 平均を取れば良いのです。そうして、次のような確率的勾配降下法の正規化された学習規則が得られます (c.f. 式 (20)\begin{eqnarray} w_k & \rightarrow & w_k' = w_k-\frac{\eta}{m} \sum_j \frac{\partial C_{X_j}}{\partial w_k} \nonumber\end{eqnarray})：

\begin{eqnarray} w \rightarrow \left(1-\frac{\eta \lambda}{n}\right) w -\frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial w}. \tag{86}\end{eqnarray}

ここで、和はミニバッチに含まれる訓練例 $x$ について取り、$C_x$ は各訓練例の （正規化されていない）コストを表します。これは、$1-\frac{\eta \lambda}{n}$ という重み減衰因子を除いて、 確率的勾配降下法のこれまで使ってきた規則と全く同じです。最後に念のため、 バイアスの学習に関する正規化された学習規則を述べておきましょう。これはもちろん、 正規化されていない規則と全く同じです (c.f. 式 (21)\begin{eqnarray} b_l & \rightarrow & b_l' = b_l-\frac{\eta}{m} \sum_j \frac{\partial C_{X_j}}{\partial b_l} \nonumber\end{eqnarray})：

\begin{eqnarray} b \rightarrow b - \frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial b}. \tag{87}\end{eqnarray} ここで、和はミニバッチに含まれる訓練例 $x$ について取ります。

では、正規化がどのくらいニューラルネットワークのパフォーマンスを変えるのか確かめてみましょう。 ここでは、隠れニューロンが30個、ミニバッチの大きさが $10$、学習率が $0.5$、そして クロスエントロピーをコスト関数として採用したニューラルネットワークを使います。 今回はさらに、正規化パラメータとして $\lambda=0.1$ を使用します。 コードの中で正規化パラメータを表す変数名として lmbda を用いている点には気をつけてください。 というのも、Pythonでは lambda が正規化パラメータとは関係の無い意味を持つ予約語だからです。 また、ここでは再び validation_data ではなく test_data を用いました。 既に議論したように、厳密に言えば validation_data を使うべきです。 今回 test_data を使うのは、そうすることで正規化する前の結果とより直接的な比較が可能になるためです。 このコードを validation_data を使うように書き換えるのは容易ですし、 実際にそうしても同様の結果が得られることがわかるでしょう。

>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data[:1000], 400, 10, 0.5,
... evaluation_data=test_data, lmbda = 0.1,
... monitor_evaluation_cost=True, monitor_evaluation_accuracy=True,
... monitor_training_cost=True, monitor_training_accuracy=True)

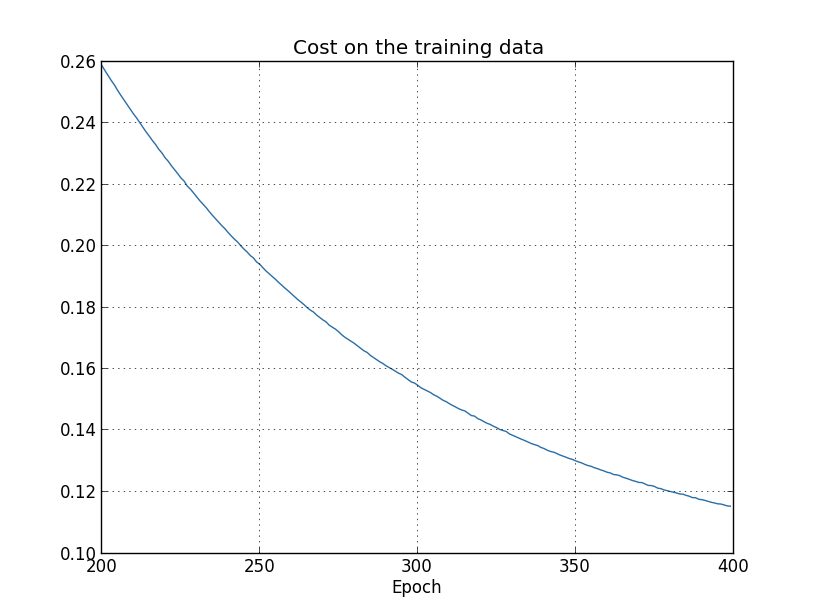
しかし今回は、test_data に対する精度も400エポックが終わるまで向上し続けています：

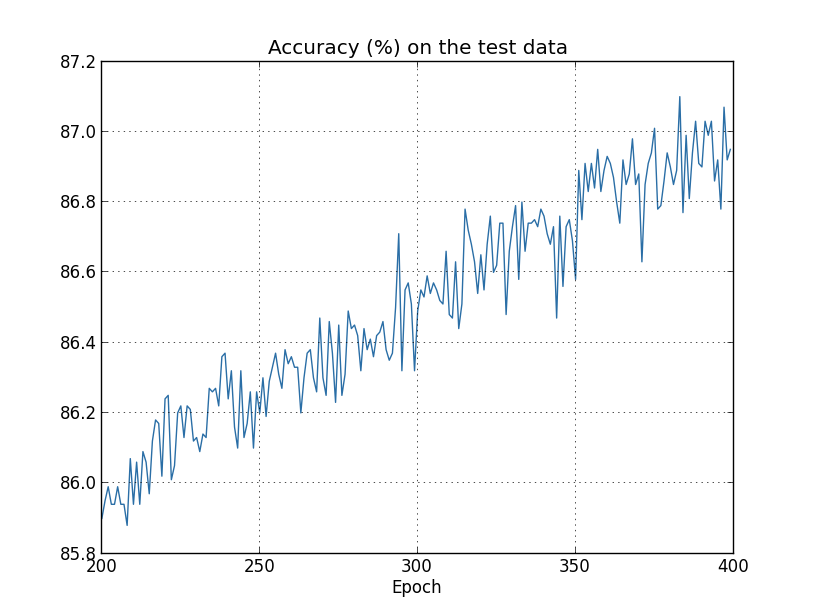
明らかに、正規化することで過適合が抑制されています。そしてそれ以上に、精度もかなり良くなっています。 ピーク時の分類精度が正規化無しで $82.27$パーセントだったのに対し、 正規化した後は$87.1$パーセントに向上しています。実は、400エポックを超えて訓練し続けることで、 目に見える改善がほぼ間違いなく得られるでしょう。経験的には、正規化することで ニューラルネットワークはより良く汎化するようになり、過適合の効果もかなり軽減されるようです。

では、訓練画像を1,000枚に制限するのをやめて、50,000枚全ての訓練データを使うことにすると 何が起こるでしょうか。もちろん既に見たとおり、50,000枚全ての画像を使えば過適合はそれほど 問題になりません。その状況で、果たして正規化にご利益があるのでしょうか？ ハイパーパラメータは前回と同じ、30エポック、学習率 $0.5$、ミニバッチの大きさは $10$、を使う ことにします。しかし、正規化パラメータは変更する必要があります。なぜなら、 訓練データの大きさを $n=1,000$ から $n=50,000$ に変更したため、そのことが重み減衰因子 $1 - \frac{\eta \lambda}{n}$ を変えているためです。もし $\lambda =0.1$ を使い続けたならば、 重み減衰はずっと抑えられて、正規化の効果もずっと小さなものになるでしょう。 訓練データの大きさの違いを埋め合わせるため、$\lambda=5.0$ を使うことにします。

さあ、今一度重みを初期化してから、ニューラルネットワークを訓練しましょう：

>>> net.large_weight_initializer()
>>> net.SGD(training_data, 30, 10, 0.5,
... evaluation_data=test_data, lmbda = 5.0,
... monitor_evaluation_accuracy=True, monitor_training_accuracy=True)

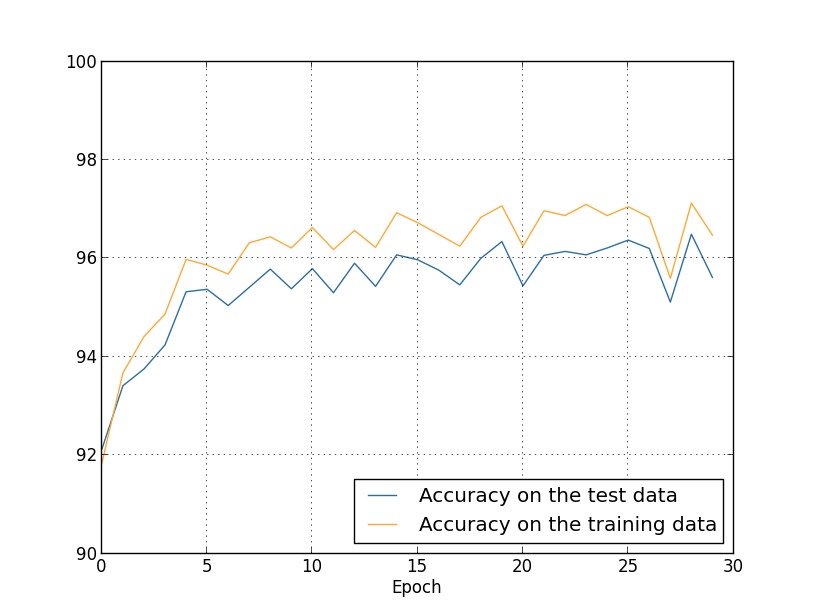
良い知らせがあります。それもたくさん。第一に、試験データに対する分類精度が、 正規化する前の $95.49$ パーセントから $96.49$ パーセントに上昇しています。 これは大きな改善です。第二に、訓練データと試験データに対する結果の差が、 正規化する前と比べてずっと小さくなっていることが見て取れます。その差は今や $1$ パーセントにも 満たない小さなものです。これでもはっきりとした差は残っていますが、 過適合を改善するという意味ではかなりの進歩です。

最後に、隠れニューロンを100個にして正規化パラメータを $\lambda=5.0$ のままにした時、 試験データの分類精度がどうなるか見てみましょう。ここでは、過適合に関する詳細な分析は行いません。 ただのお楽しみとして、クロスエントロピーコスト関数とL2正規化という2つの新しい手法が どれだけの精度をもたらすのか見てみるのが、ここでの目的です。

>>> net = network2.Network([784, 100, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data, 30, 10, 0.5, lmbda=5.0,
... evaluation_data=validation_data,
... monitor_evaluation_accuracy=True)

最終的に得られる分類精度は、検証データに対して $97.92$ パーセントです。 これは隠れニューロンが30個だった時と比べると大きな飛躍です。実は、もう少しだけチューニングして、 $\eta=0.1$ と $\lambda=5.0$ にセットして60エポック走らせると、 検証データに対する分類精度が $98$ パーセントの壁を超えて、 $98.04$ パーセントという結果を実現します。たった152行のコードにしては悪くない仕事ですね！

ここまで私は、正規化を過適合を防ぎ分類精度を向上させるための手法として説明してきました。 実は、正規化のご利益はそれだけではありません。 ここで作成したMNISTを分類するニューラルネットワークを、 重みの初期値をランダムに変えながら繰り返し走らせてみましょう。 実際にやってみて私が気づいたのは、正規化しないと時折「引っかかる」ことです。 つまり、コスト関数の極小に捕らえられているようなのです。 結果として、異なる初期値から始めると時々かなり異なる結果に行き着くことになります。 対照的に、正規化した場合にはより簡単に再現可能な結果が得られます。

なぜこのようなことが起こるのでしょうか？ヒューリスティックには、 もしコスト関数が正規化されていないと、重みベクトルの長さは大きくなりがちです。 時間が経つにつれ、実際に重みベクトルはかなり大きくなりえます。 重みベクトルが長い時、勾配降下法はその動径方向に向かいやすく、 重みベクトルの向きを変える方向にはわずかにしか動きません。このため、 一旦重みベクトルが長くなってしまうと、重みベクトルが同じ方向を向いて 動かなくなってしまう可能性があります。この現象が原因で、 私たちが使っている学習アルゴリズムでは重み空間を十分に探索することができず、 結果的にコスト関数の良い最小値を見つけるのが困難になっているのではないかと、 私は考えています。

なぜ正規化で過適合が軽減されるのか？

実際に正規化を実装してみることで、確かに正規化によって過適合が軽減されることを見てきました。 この結果には勇気づけられますが、残念ながら、なぜ正規化が過適合を軽減してくれるのか明白とは言えません。 この点についてしばしばなされる説明は次のようなものです。「重みがより小さいということは、ある意味で、 複雑さがより小さいことを意味し、それゆえ、より単純で強力にデータを説明してくれるのだ。」 ただ、この説明はずいぶん簡潔で、曖昧で誤魔化されているようにも思えます。 ですから、この説明を批判的に検証してみましょう。 そのために、次のような単純なデータセットを用意して、これを説明するモデルの構築してみましょう：

私たちはここで、暗にある現実の現象を調べています。そして、$x$ と $y$ は現実のデータを表しています。 ここでの目標は、$x$ の関数として $y$ を予言するモデルの構築です。 そのためにニューラルネットワークを用いることも可能ではありますが、 今はもっと単純なことを考えます：$y$ を $x$ の多項式としてモデル化してみます。 ニューラルネットワークの代わりに多項式を利用するのは、 多項式は何が起こっているのか特に見やすいためです。 そこで、まずは多項式で起こっていることを理解してから、 それをニューラルネットワークに翻訳しようと思います。 今、上のグラフには10個のデータ点があるので、 これらの点を全て通過する9次多項式 $y = a_0 x^9 + a_1 x^8 + \ldots + a_9$ がただ一つに定まります。 これがその多項式のグラフです* *ここでは多項式の係数を明示しませんが、例えば Numpy に含まれる polyfit 等の ルーチンを使って簡単に係数を計算できます。 もし興味があれば、多項式の正確な形はグラフのソースコードで 見ることが出来ます。グラフを生成するプログラムの14行目から定義されている関数 p(x) です。：

この多項式はデータ点を正確にフィッティングしています。 しかし、これらのデータ点は $y = 2x$ という直線を使っても良くフィッティングできます：

この2つのうち、どちらがより良いモデルであると言えるでしょうか？ どちらがよりもっともらしく、真実に近いのでしょうか？ そして、同じ現実の現象の他の例に対して、どちらのモデルがより良く汎化できるでしょうか？

これらは難しい質問です。実は、どの質問に対しても、確証を持って答えることは出来ません。 そうするには、背後にある現実の現象に関する情報がもっと必要です。 しかし、2つの可能性を考えてみましょう：(1) 実は9次多項式が本当に現実の現象を記述するモデルになっていて、 したがって他の例に対しても完璧に汎化できる可能性、そして (2) 正しいモデルは $y=2x$ なのだが、例えば測定の誤差などに起因するノイズが乗っているため、 モデルがデータ点を完全にはフィットしていない可能性、です。

どちらが正解だと言い切る根拠はありません（あるいは、どちらでもない、 第3の可能性もありうるかもしれません）。論理的には、どちらでもありうるのです。 にも関わらず、両者の違いは決して些細なものではありません。 確かに、データ点の与えられている領域では2つのモデルの予言には小さな違いしかありません。 しかし、もしも上のグラフで示されているよりももっとずっと大きな $x$ に対して $y$ を予言したいとしたら、 どうでしょうか。その時には、両者の予言の間にはとてつもない違いが生じるでしょう。 なぜならば、9次多項式では $x^9$ の項が支配的になりますが、 線形モデルは、なんというか、線形のままですから。

一つの立場は、どうしても複雑なモデルを採用しなければならない特段の事情がない限り、 科学においてはより単純な説明を採用するのが望ましいという考え方です。 多くのデータ点を説明できる簡単なモデルが見つかった時には、「エウレカ！」と叫びたい 衝動に駆られるでしょう。なんといっても、単純な説明とデータが単なる偶然の一致を見せるとは、 考えにくいように思われます。むしろ、そのモデルは現象の背後にある何らかの真理を言い当てている と信じたくなるでしょう。今考えている例では、$y=2x+\text{(ノイズ)}$ というモデルは $y=a_0x^9 + a_1 x^8 + \ldots$ よりずっとシンプルに見えます。 そんな単純さが偶然に現れたのだとすると驚きです。だからこそ、 私たちは $y=2x+\text{(ノイズ)}$ が背後にある何らかの真理を表していると期待するのです。 この立場に基づくと、9次多項式モデルは局所的なノイズの効果を学習しているに過ぎません。 だから、9次多項式モデルは与えられたデータ点を完璧に説明はするけれども、 他のデータ点に対して汎化はできないでしょう。そして、ノイズ付き線形モデルが より強力な予言能力を持つでしょう。

この立場がニューラルネットワークにおいて何を意味するのか見てみましょう。 正規化されたニューラルネットワークで期待されるように、 ニューラルネットワークの大部分では小さな重みを持つと仮定しましょう。 重みが小さいということは、ここそこでランダムな入力を変化させても ニューラルネットワークの振る舞いが大きくは変わらないことを意味します。 そのため、正規化されたニューラルネットワークでは、 データに含まれる局所的なノイズの効果を学習しづらくなっています。 その代わり、正規化されたニューラルネットワークは訓練データの中で繰り返し見られる データの特徴に反応するのです。対照的に、大きな重みを持つニューラルネットワークは、 入力の小さな変化に敏感に反応してその振る舞いを大きく変えてしまいます。 そのため、正規化されていないニューラルネットワークは、大きな重みを使って、 訓練データのノイズに関する情報をたくさん含んだ複雑なモデルを学習してしまうのです。 要するに、正規化されたニューラルネットワークは訓練データに頻繁に現れるパターンに基づいた 比較的シンプルなモデルを構築します。そして、訓練データが持つノイズの特異性を学ぶことに対して 耐性を持つのです。このため、ニューラルネットワークがノイズではなく現象そのものに対する真の学習をして、 それをより良く汎化できるのではないかと、希望が持てます。

ここまで説明したところで、よりシンプルなモデルが好ましいという考え方に不安を感じるかもしれません。 この考えはしばしば「オッカムの剃刀」と呼ばれ、何か一般的な科学の原理であるかのように扱われます。 しかし、もちろん、これは一般的な科学の原理ではありません。 複雑なモデルよりも単純なモデルを好むべき、ア・プリオリな論理的理由は無いのです。 実際、より複雑な説明が正しいという場合もあるのです。

結果的には複雑な説明の方が正しかったという例を2つ紹介しましょう。 1940年台に物理学者のマルツェル・シャインは新粒子を発見したと主張しました。 彼が働いていたゼネラル・エレクトリック社はすっかり盛り上がって、 その発見を広く宣伝しました。しかし、物理学者のハンス・ベーテは懐疑的でした。 ベーテはシャインの元を訪れ、シャインの新粒子の飛跡が残るプレートを調べました。 シャインは次々にプレートを見せましたが、 ベーテはそれぞれのプレートにデータとして採用すべきでない理由を見出しました。 最後に、シャインは問題なさそうに見えるプレートを差し出しました。 ベーテは、それが統計的なまぐれ当たりに過ぎないのではないかと言いました。 シャイン：「そうかもしれないが、その確率はあなたの公式によると5分の1しかありません。」 ベーテ：「しかし、もう既に5つのプレートを見ました。」 そこでシャインは次のように言いました：「しかし、あなたは一つ一つのプレート、 一つ一つの写真に対して異なる理論で批判をしました。 ところが、それらが新粒子であるというたった一つの仮説は、全てのプレートを説明します。」 ベーテは次のように答えました：「あなたと私のたった一つの違いは、 あなたの説明は間違っているが、私の説明は全てが正しいということです。 あなたのただ一つの説明は間違いですが、私の複数の説明は正しいのです。」 後の研究により、ベーテが正しかったことが確かめられました* *この話は、物理学者のリチャード・ファインマンが歴史家のチャールズ・ワイナーとの インタビュー の中で紹介したものです。。

2つ目の例として水星の軌道にまつわる話を紹介します。 天文学者のユルバン・ルヴェリエは1859年に水星の軌道がニュートンの重力理論による 予測と一致しないことを発見しました。そのズレは本当に、本当に僅かなもので、 当時よく見られた説明は、つまるところ、ニュートンの重力理論はだいたい正しく、 しかし僅かな修正が必要であるというものでした。 1916年に、アインシュタインはそのズレが彼の一般相対性理論を使うととてもよく 説明できることを示しました。ところが、一般相対性理論はニュートンの重力理論と 根本的に異なっており、ずっと複雑な数学に基づいていました。 このようにとても複雑な一般相対性理論ですが、今日ではアインシュタインの説明が 広く受け入れられています。そして、ニュートンの理論は修正されたものも含めて間違っていると 考えられています。これは一つには、アインシュタインの理論がニュートンの理論では 説明が困難な他の多くの現象を説明できるためです。そしてさらに、 ニュートンの重力では全くもって予言できない現象を正確に予言できるのです。 しかし、これらの印象的な性質は、初期の頃から明らかであったわけではありません。 もし単純さのみに基づいて判断していたら、おそらくいずれかの修正されたニュートン理論が もっと魅力的に映ったことでしょう。

これらの逸話から3つの教訓が得られます。 第1に、2つのモデルのどちらが真に「より単純」かを決めるのは、 非常に微妙な問題であること。第2に、もしそのような判断を下すことができたとしても、 単純さが正しさの指標になりうるかどうかは注意深く検討する必要があること。 第3に、モデルを測る本当の尺度は単純さではなく、 未知の領域で新しい現象をどれほど良く予言できるかという点であることです。

これらの注意を頭の片隅においておいて、経験的な事実として、 正規化したニューラルネットワークは通常、正規化されていないニューラルネットワークよりも よく汎化するのだと言っておきます。なので、この本の残りの部分では頻繁に 正規化を利用します。私が上でいくつかの逸話を紹介したのは、 正規化によってニューラルネットワークの汎化が助けられることについて、 完全に納得できる理論的な説明が存在しないことを伝えるためなのです。 実は、研究者は新しい正規化の手法を試しては、それらを比較してどちらがより良いか調べ、 その理由を理解しようと試みています。ですから、正規化は今の段階ではある種の その場しのぎであるとみなすこともできます。 正規化は仕事の助けになりますが、正規化によって実際に何が起こっているのかについて、 完全に満足の行く系統的な理解は無く、不完全なヒューリスティックと経験則しかないのです。

ここには科学の核心に関わる、さらに深い論点があります。 それは、私たちが経験的な理解をどう汎化するのかという問いです。 正規化は上手く計算するための魔法のようなもので、 それは確かにニューラルネットワークが汎化するのを助けますが、 どのように汎化しているのかという原理に関する理解も、 何が最良のアプローチなのかという答えも教えてはくれないのです* *これらの論点は、スコットランド人の哲学者、デイビッド・ヒュームによって "An Enquiry Concerning Human Understanding" (1748) の中で議論された、帰納法の問題に 遡ります。帰納法の問題は、現代の機械学習においては、 デイビッド・ウォルパートとウィリアム・マクレディーによるノーフリーランチ定理として現れます。 (リンク) 。

このことが一際悩ましく思えるのは、私たち人間が日常的に驚くほどうまく汎化するからです。 象の画像をほんの数枚見ただけで、子供はすぐに他の象を認識し始めるでしょう。 もちろん、時には間違えもするでしょうし、サイを象と混同するかもしれません。 それでも多くの場合に非常に正確でしょう。つまり、ここに一つのシステム、 すなわち人間の脳があって、それは莫大な数のパラメータを持ちます。 そしてそれは、たった数枚の訓練画像を見せられるだけで、 このシステムは他の画像に対して汎化しはじめるのです。 私たちの脳はある意味で、非常に上手く正規化されているのです！ どうすれば私たちにもニューラルネットワークで同じことができるでしょうか？ 現時点では分かりません。向こう数年のうちに、人工的なニューラルネットワークを 正規化するより強力な手法が開発されて、 究極的にはわずかな訓練データから良く汎化できるようになると期待します。

実は、これまで実装してきたニューラルネットワークは、 既にア・プリオリに期待されるよりも良く汎化しています。 100個の隠れニューロンを持つニューラルネットワークには、80,000個近いパラメータがあります。 訓練データには50,000枚の画像しかありません。いわば、80,000次多項式で50,000個のデータ点を フィットしようとしているようなものです。本来なら、このニューラルネットワークはひどく 過適合を起こしても当然なわけです。にも関わらず、これまで見てきたように非常に良く汎化するのです。 なぜこんなことが起こるのでしょうか？これはよく理解されているわけではありません。 「多層ニューラルネットワークにおける勾配降下学習のダイナミクスには 『自己正規化』効果がある」という仮説はあります* *出典は Gradient-Based Learning Applied to Document Recognition, by Yann LeCun, Léon Bottou, Yoshua Bengio, and Patrick Haffner (1998) です。。

この節の終わりに、ここまで説明せずに来た詳細に戻ってきましょう： なぜL2正規化でバイアスを制限しないのでしょうか？ もちろん、バイアスを正規化するように正規化の手順を修正するのは簡単です。 経験的には、そうしても結果が大きく変わらないので、 バイアスを正規化するかどうかは単なる慣例であるということも出来ます。 しかし、次の事実には言及しておく価値があるでしょう。 それは、バイアスが大きくなっても、重みが大きくなった時のように 入力に対するニューロンの感受性が高まるわけではない、という事実です。 だから、大きなバイアスのために訓練データのノイズを学習してしまうのではないかと 心配する必要は無いわけです。同時に、大きなバイアスを許すことで、 ニューラルネットワークはより柔軟に振る舞えるようになります。 特に、大きなバイアスを許すことでニューロンの出力が容易に飽和できるようになります。 時にこの性質が望ましい場合があります。 これらの理由から、普通はバイアス項を正規化に含めません。

その他の正規化手法

正規化の手法はL2正規化以外にもたくさんあります。 実は、余りにたくさんありすぎて、その全てを要約することはできそうもありません。 この節では、3つの手法、L1正規化、ドロップアウト、そして人工的な学習データの伸張、 に的を絞って手短に紹介します。ここではL2正規化についてしてきたような詳細な説明はしません。 その代わり、ここでの目的は主要なアイデアに親しんでもらうことと、 正規化手法の多様性を認識してもらうことです。

L1正規化： このアプローチでは、 正規化する前のコスト関数に重みの絶対値の和を足します：

\begin{eqnarray} C = C_0 + \frac{\lambda}{n} \sum_w |w|. \tag{88}\end{eqnarray}

直感的には、大きな重みを不利にし、ニューラルネットワークが小さな重みを好むように仕向けるという意味で、 L2正規化と似ています。もちろん、L1正規化項はL2正規化項と同じではないので、 両者が全く同じ振る舞いをするわけでもありません。 L1正規化して訓練したニューラルネットワークの振る舞いがL2正規化の場合とどう違うのか見てみましょう。

そのために、まずはコスト関数の偏微分を調べましょう。 式(88)\begin{eqnarray} C = C_0 + \frac{\lambda}{n} \sum_w |w| \nonumber\end{eqnarray} を微分して、次の表式が得られます： \begin{eqnarray} \frac{\partial C}{\partial w} = \frac{\partial C_0}{\partial w} + \frac{\lambda}{n} \, {\rm sgn}(w). \tag{89}\end{eqnarray}

ここで、${\rm sgn}(w)$ は $w$ の符号、つまり、$w$ が正なら $+1$ で負なら $-1$ です。 この表式を使うと、L1正規化を使った確率的勾配降下法を実行するように逆伝播法を修正できます。 そうやって求めたL1正規化の下での更新規則は、 \begin{eqnarray} w \rightarrow w' = w-\frac{\eta \lambda}{n} \mbox{sgn}(w) - \eta \frac{\partial C_0}{\partial w} \tag{90}\end{eqnarray}

です。ここでいつも通り、$\partial C_0 / \partial w$ をミニバッチ平均によって評価することができます。 これをL2正規化を用いた更新規則と比べてみましょう： (c.f. 式 (86)\begin{eqnarray} w \rightarrow \left(1-\frac{\eta \lambda}{n}\right) w -\frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial w}, \nonumber\end{eqnarray}), \begin{eqnarray} w \rightarrow w' = w\left(1 - \frac{\eta \lambda}{n} \right) - \eta \frac{\partial C_0}{\partial w}. \tag{91}\end{eqnarray} どちらの表式でも、正規化の効果は重みを縮小することだとわかります。 この点は、どちらの正規化も大きな重みを不利にするという直感と整合します。 しかし、縮小の仕方が異なります。L1正規化は、重みを0の方向に一定の大きさだけ縮小します。 L2正規化では、重みは $w$ に比例する量だけ縮小します。そのため、 特定の重みが大きな絶対値 $|w|$ を取っている時に、L1正規化はL2正規化と比べるとほんのわずかにしか $w$ の値を変化させません。 反対に、ある重みが小さな絶対値 $|w|$ を持っている時には、L2正規化よりもずっと大きく $w$ の値を変化させます。 全体としては、L1正規化をした後のニューラルネットワークでは、一部の比較的少数の重要なリンクに重みに集中し、 他の重みは0の方に追いやられることになります。

ここまでの議論で、偏微分 $\partial C / \partial w$ が $w=0$ で定義されないことについて 敢えて触れずに来ました。関数 $|w|$ は $w=0$ に尖った「角」があるので、 この点で微分不可能なのです。とはいえ、実はこのことは問題ありません。 もし $w=0$ なら、その点で通常の（正規化していない）規則を使って確率的勾配降下法を行えば良いのです。 この方法なら問題無いでしょう。というのも、直感的には正規化の効果が重みを縮小することなら、 $w=0$ では明らかにこれ以上縮小のしようが無いからです。より正確には、 式 (89)\begin{eqnarray} \frac{\partial C}{\partial w} = \frac{\partial C_0}{\partial w} + \frac{\lambda}{n} \, {\rm sgn}(w) \nonumber\end{eqnarray} と (90)\begin{eqnarray} w \rightarrow w' = w-\frac{\eta \lambda}{n} \mbox{sgn}(w) - \eta \frac{\partial C_0}{\partial w} \nonumber\end{eqnarray} の中で、$\mbox{sgn}(0) = 0$ という定義を採用します。 そうすることで、L1正規化して確率的勾配降下法を実行するコンパクトな規則が出来上がります。

ドロップアウト： ドロップアウトは、これまで紹介してきたものとは全く違う正規化の手法です。 L1正規化やL2正規化と違って、ドロップアウトでは元のコスト関数をそのまま使います。 その代わり、ドロップアウトではニューラルネットワークそのものを修正します。 まずはドロップアウトの基本的な仕組みを説明してから、 なぜドロップアウトで上手くいくのか、そしてどのような結果をもたらすのかを説明します。

あるニューラルネットワークを訓練しようとしていると仮定しましょう：

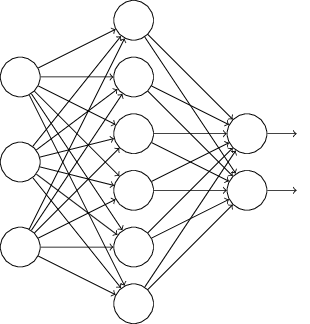
特に、訓練入力 $x$ とそれに対応する正解の出力 $y$ を知っているとします。 通常、ニューラルネットワークを訓練するためにまず $x$ を順伝播させて、 次に勾配を求めるために逆伝播を行います。ドロップアウトではこのプロセスを修正します。 まず、ランダムに（そして一時的に）ニューラルネットワークの隠れニューロンを半分削除します。 このとき入力・出力ニューロンは削除せずにそのままにしておきます。 すると、下に示したようなニューラルネットワークが得られます。 ここで、抜け落ちた（ドロップアウトした）ニューロン、つまり一時的に削除された ニューロンは、点線で残してあることに注意してください：

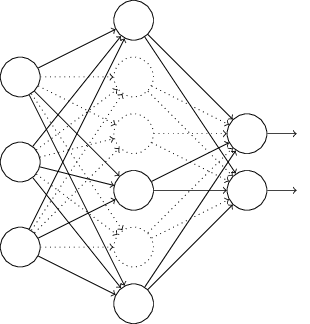
その後、入力 $x$ を修正されたニューラルネットワークで順伝播させ、 次にその結果を再び修正後のニューラルネットワークで逆伝搬させます。 ミニバッチに含まれる全ての例についてこれを実行した後、 削除されずに残っている重みとバイアスを更新します。 そしてこの過程を繰り返します。つまり、まずドロップアウトしたニューロンを戻し、 削除するニューロンを再びランダムに選び直し、新しいミニバッチを用いて勾配を評価し、 ニューラルネットワークの重みとバイアスを更新します。

これを繰り返すことで、ニューラルネットワークは重みとバイアスを学習します。 もちろん、ここで得られた重みやバイアスは、 隠れニューロンの半分がドロップアウトしているという条件の元で学習した結果です。 実際にニューラルネットワークの全体を動かすと、2倍のニューロンが有効になります。 この点を補うために、隠れニューロンから出て行く重みを半分にします。

このドロップアウトの手続きは奇妙でアドホックに思えるかもしれません。 なぜこれが正規化を助けるのでしょうか？何が起こっているのか説明するために、 一旦ドロップアウトについて考えるのをやめて、ドロップアウト無しに 通常の方法でニューラルネットワークを訓練することを想像してみてください。 特に、複数のニューラルネットワークを同じ訓練データで訓練する 状況を考えてみましょう。もちろん、それぞれのニューラルネットワークは 全く同じものではありませんから、 結果として訓練した後のニューラルネットワークから得られる出力も ニューラルネットワークごと異なるかもしれません。 そうなった時には、何らかの平均化や多数決のような手法を用いることで どの出力を採用するか決定できるでしょう。例えば、5つのニューラルネットワークを 訓練して、そのうち3つが数字の画像を "3" に分類したとすると、その時は おそらく実際に "3" なのでしょう。残り2つのニューラルネットワークは 単に間違えてしまっただけだと思われます。この種の平均化の手法は、 しばしば過適合を軽減する強力な（しかし負担も大きい）手法です。 異なるニューラルネットワークは異なる過適合のしかたをすることがあるので、 平均化がこの種の過適合を防ぐ助けになるのです。

これとドロップアウトがどう関係するというのでしょうか？直感的には、 異なるニューロンの組み合わせをドロップアウトしてから訓練するのは、 異なるニューラルネットワークを訓練しているようなものです。 だから、ドロップアウトの手続きは、大量の異なるニューラルネットワークの結果を 平均化しているようなものであると見なせます。異なるニューラルネットワークは 違った過適合のしかたをするでしょうから、上手くいけば全体としては過適合が軽減されるでしょう。

これと関連するヒューリスティックな説明は、この手法を用いた最初期の論文で与えられています *ImageNet Classification with Deep Convolutional Neural Networks, by Alex Krizhevsky, Ilya Sutskever, and Geoffrey Hinton (2012).： 「この手法はニューロン間の複雑な相互適合を軽減します。というのも、 訓練に際してニューロンは特定の他のニューロンを頼りにすることができないからです。 したがって、あるニューロンは、ランダムに選ばれた他のニューロンと一緒にされても役に立つような、 データが持つより強固な特徴を学ぶように強制されるのです。」 ニューラルネットワークのことを何らかの予言をするモデルだと見なすなら、 ドロップアウトは入力される情報の欠落に対して強いモデルを作る方法だと言うことができるでしょう。 この点において、何となくL1正規化やL2正規化と似ているとも言えます。 これらの手法は、重みを小さくすることで、ニューロン間の接続を失うことに対して ニューラルネットワークを強くしていると言えるからです。

もちろん、ドロップアウトの実力を測る真の尺度は、それがニューラルネットワークの パフォーマンス改善に大きな成功を収めてきたという点です。 この手法を導入した原論文* *Improving neural networks by preventing co-adaptation of feature detectors by Geoffrey Hinton, Nitish Srivastava, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov (2012). この論文では、 このドロップアウトに関する短い紹介文ではあえて触れずに来た 多くの繊細な点についても議論しています。 では、様々な異なるタスクにこの手法を適用しています。 私たちにとっては、彼らがドロップアウトをMNISTの分類問題に適用していることが 特に興味深いところです。彼らはシンプルなフィードフォワードニューラルネットワークを使って、 私たちがやってきたのと同じようなことをしています。 論文には、その時点で達成されていた試験データに対する最高の分類精度が $98.4$ パーセントであると 書いてあります。彼らはドロップアウトと修正されたL2正規化を組み合わせて、 それを $98.7$ パーセントに改善しました。同様に印象的な結果が画像や音声認識、自然言語処理 などたくさんの他のタスクに関しても得られています。 ドロップアウトは過適合の問題が深刻になる巨大で多層のニューラルネットワークを訓練するときに、 特に有用になります。

人工的な学習データの伸張: 前に確かめたように、訓練画像が1,000枚しか無いと MNISTの分類精度は80パーセント中盤にまで減少してしまいます。このこと自体は驚くべきことではありません。 訓練データが少ない分、ニューラルネットワークが学ぶ手書き文字のバリエーションも少なくなるからです。 では、30個の隠れニューロンを持つニューラルネットワークを異なるサイズの訓練データセットで 訓練したら、分類精度はどのように変化するでしょうか。ここでは、ミニバッチの大きさを10、 学習率を $\eta = 0.5$、正規化パラメータを $\lambda=5.0$ とし、コスト関数にはクロスエントロピーを 使うことにします。訓練データセットの全体を使うときには訓練を30エポック回します。 訓練データを小さくするのに反比例するように、エポック数を大きくすることにします。 重み減衰因子が訓練データセットの大きさに依らず一定になるように、全訓練データを用いるときには $\lambda = 5.0$ とし、小さい訓練データセットを使うときには そのサイズに比例して $\lambda$ を小さくすることにします* *これと次のグラフはプログラム more_data.py が生成したものです。。

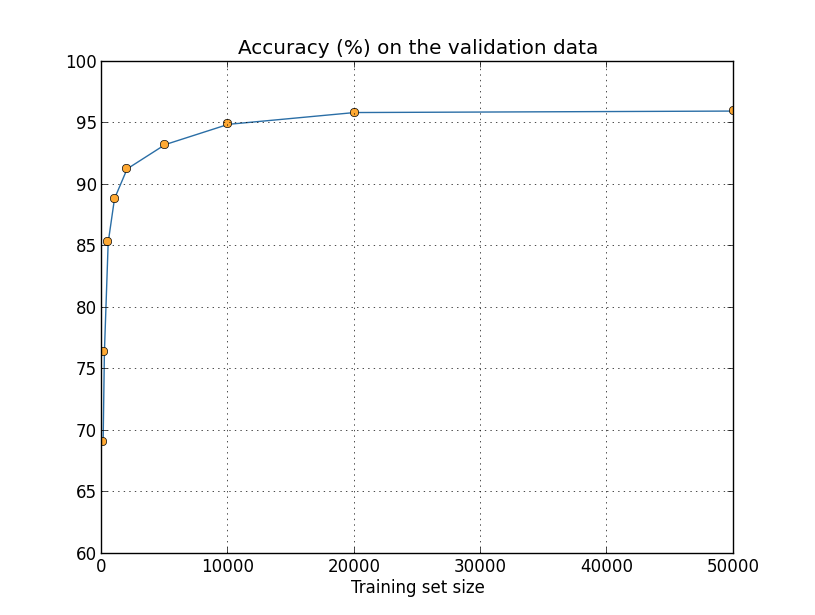
見て分かるように、より多くの訓練データを使うことで分類精度はかなり改善されます。 おそらく、訓練データをさらに増やすことでこの改善はまだまだ続くでしょう。 上のグラフを見るとほとんど飽和しているようにも見えますが、 横軸を訓練データサイズの対数にしてプロットし直すと、次のグラフが得られます：

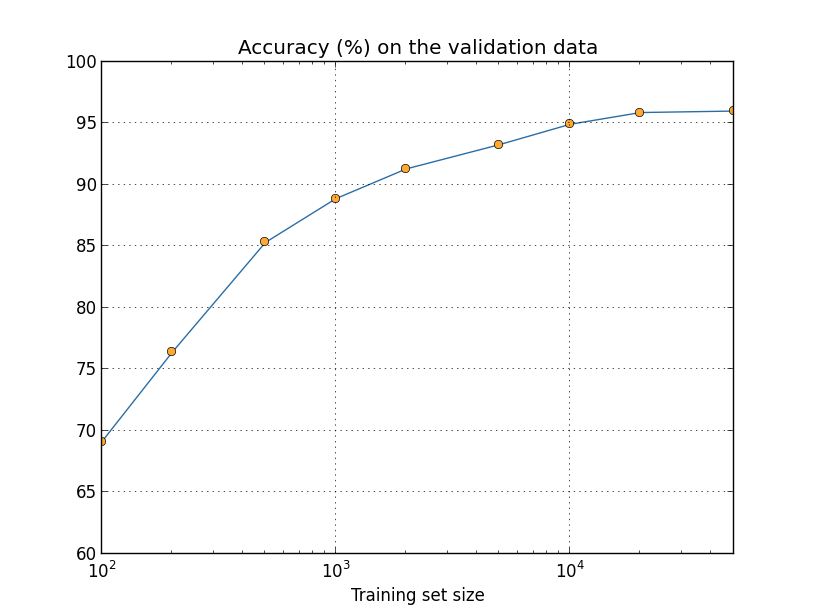
こうしてみると、終わりに向けてまだグラフが上昇しているのが明らかになります。 もしもっと莫大な数の訓練データを使えたら、例えば、100万も10億も手書きの数字を集められたら、 このとても小さなニューラルネットワークでもかなり良いパフォーマンスを発揮するでしょう。

訓練データをもっと集めようというのは素晴らしいアイデアです。ただ残念なことに、 それはとても負担が大きく、現実的にはいつでも実行できることではありません。 しかし、訓練データを集めるのと同じくらい効果的な別の方法があります。 例えば、MNISTの訓練画像から「5」の画像を一枚取り出してみましょう。

そして、この画像を少しだけ、例えば15度回転させてみます：

私たちが見れば、まだこの画像が同じ数字を表していると分かります。それでも、ピクセル単位で見ると、 MNISTに含まれるどの画像ともかなり異なります。この画像を訓練データに加えれば、 これからニューラルネットワークは数字の分類についてより多く学ぶだろうことは想像に難くありません。 さらに、訓練データに加えて良いのはこの1枚だけではありません。 全てのMNIST訓練画像についてたくさんの小さな回転を施して、 元の訓練データを拡張することができます。 そしてこの拡張された訓練データを使ってニューラルネットワークのパフォーマンスを改善できるのです。

このアイデアは非常に強力で広く使われています。ある論文* *Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis, by Patrice Simard, Dave Steinkraus, and John Platt (2003).から幾つかの結果を紹介しましょう。この論文では、 訓練データを拡張する方法の幾つかの変種をMNISTに適用しています。 彼らが考えたニューラルネットワークの構造は、私たちが使ってきたものと似た フィードフォワードニューラルネットワークで、800個の隠れニューロンを持ち コスト関数にはクロスエントロピーを使っています。 通常のMNIST訓練データでニューラルネットワークを訓練した時には、 彼らは試験データに対して98.4%の分類精度を達成しました。しかし、次に訓練データを 上で説明したような回転に加えて、平行移動と歪みで拡張しました。 拡張された訓練データでニューラルネットワークを訓練すると、98.9% の分類精度を達成しました。 彼らはさらに、彼らが「弾性歪み」と呼んだ変形を使って実験しました。これは 手の筋肉で起こるランダムな振動を模倣する、特別な変形です。訓練データの拡張に弾性歪みを使うことで、 さらに改善して99.3%という分類精度を達成しました。 彼らが行ったことは、実際の手書き文字に見られるバラつきに触れさせることで ニューラルネットワークに実質的により多くの手書き文字を経験させていたと言えます。

このアイデアの仲間は、手書き文字認識に限らず多くの機械学習のタスクで パフォーマンスを改善するために使うことができます。基本的な原理は、現実的なデータに見られる バラつきを反映するような操作を訓練データに行い、訓練データを拡張するということです。 これをどう実行するか考えるのは難しいことではありません。 例えば、音声認識を行うニューラルネットワークを作っているとしましょう。 私たち人間は、背後に雑音があっても会話を認識できます。ですから、雑音を加えてデータを拡張できます。 また、人間は会話の速度が早くても遅くても、会話を認識できます。 したがってこれも訓練データを拡張する一つの方法です。これらの手法はいつも使われるわけではありません。 例えば、訓練データにノイズを加えて拡張する代わりに、まずノイズ軽減フィルターを通して綺麗にした データをニューラルネットワークに入力することにした方が効率的だとしても不思議ではありません。 それでも、訓練データを拡張するという選択肢を頭の片隅においておき、 それを実行する機会を伺うのは、良い心がけです。

演習

• 上で議論したように、訓練画像を少し回転させるのはMNISTの訓練データを拡張する一つの方法です。 この時、任意の回転角を許すとどのような問題が起こるでしょうか？

ビッグデータと分類精度比較に関する余談： ニューラルネットワークの分類精度が訓練データセットの大きさによってどう変化するのか もう一度見てみましょう：

ここで、ニューラルネットワークの代わりに、何か他の機械学習手法で数字を分類することを 考えてみましょう。例えば、Chapter 1で手短に紹介した サポートベクターマシン（SVM）を使ってみましょう。SVMに馴染みがなくても心配は不要です。 ここでの議論にはその詳細を理解している必要はありません。SVMを自分で実装する代わりに、 scikit-learn ライブラリで提供されている SVMをここでは利用します。SVMのパフォーマンスが訓練データセットの大きさに関して どう変化するのかを示したのが下の図です。比較のために、ニューラルネットワークの結果も 合わせてプロットしました* *このグラフは、（これまでのいくつかのグラフと同様に）プログラム more_data.py で生成したものです。：

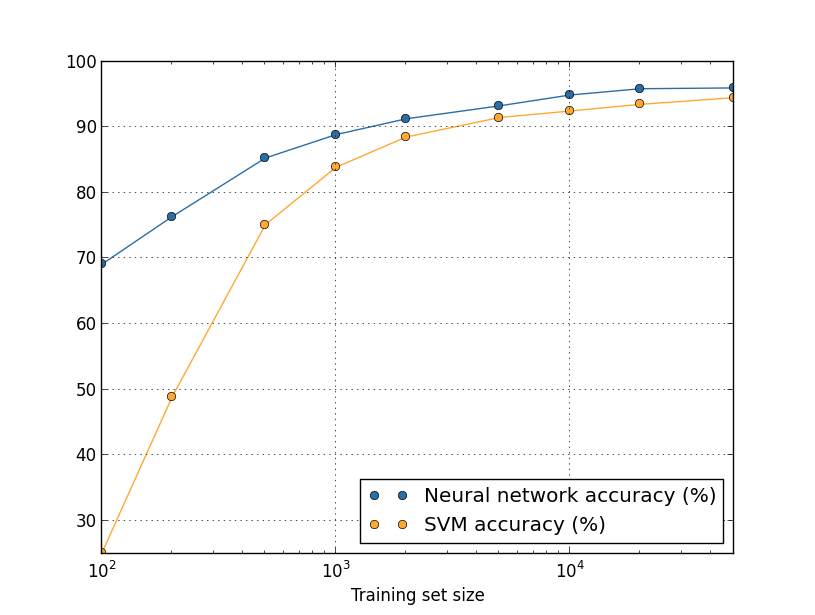
たぶんこのグラフを見てまず皆さんが驚くのは、ニューラルネットワークが どんな大きさの訓練データセットについてもSVMを大きく上回る結果を上げていることでしょう。 これは素晴らしいことではありますが、過大評価してもいけません。 というのも、私たちはニューラルネットワークのパフォーマンス改善のために様々な チューニングを施してきましたが、ここで使ったSVMについてはscikit-learnで提供されている 設定をそのまま使ったものだからです。このグラフに関するもっと微妙で、しかし興味深い事実は、 50,000枚の訓練画像を使って訓練したSVMが94.48パーセントの分類精度を達成しており、 これは5,000枚の訓練画像で訓練されたニューラルネットワークの分類精度93.24パーセントよりも 高いパフォーマンスを発揮しているという点です。言い換えるなら、 時として、より多くの訓練データを使うことで、使用している機械学習アルゴリズムの差は 埋められるということです。

時にはより一層面白いことが起こります。ある問題をアルゴリズムAとアルゴリズムBという 2つの機械学習アルゴリズムを使って解こうとしているとしましょう。時々、 ある訓練データセットではアルゴリズムAが勝ち、異なる訓練データセットではアルゴリズムBが 勝つ、ということが起こります。上のグラフではそのようなことは起きていません。 もしそうなら、2つのグラフが交差するはずです。しかし実際に、そのようなことは起こりうるのです* *次の論文の中でその顕著な例が与えられています： Scaling to very very large corpora for natural language disambiguation, by Michele Banko and Eric Brill (2001).。したがって、 「アルゴリズムAはアルゴリズムBよりも優れていますか？」と質問された時、正しい返事のし方は 「使っているデータセットは何ですか？」になります。 データセットが指定されない限り、パフォーマンスの比較はできないのです。

これらの注意は、開発を行う時にも研究論文を読む時にも心に留めておくべきです。 多くの論文では、標準的なベンチマークとなるデータセットに対するパフォーマンスを改善する 新しい手法やコツを探すことに注力しています。研究論文ではしばしば、 「我々の素晴らしい手法は、標準的なベンチマークX に対してYパーセントの改善をもたらしました」という形式を取る主張を目にします。 このような主張はしばしばそれ自体が本当に興味深いものですが、 使用した特定の訓練データセットにおいてのみ適用できるものだと理解しなければなりません。 もしこの世界とは別に、ベンチマークのデータセットを作成した人がより多くの研究資金を獲得できる 世界があったら何が起こっているでしょうか？研究者たちはより多くの訓練データを集めるために より多くのお金を掛けるかもしれません。すると、「素晴らしい手法」がもたらした「改善」が、 より大きな訓練データセットでは消滅してしまう、なんてことも、全くもってありうることなのです。 言い換えると、元々主張した「改善」は、歴史の偶然に過ぎないのかもしれません。 ここから学ぶべき教訓は、特に実際の応用においては、より良いアルゴリズムとより良い 訓練データがどちらも必要なのです。より良いアルゴリズムを追求するのは構いませんが、 より多くの訓練データを集めることでより簡単に目標を達成できる可能性を見落として、 アルゴリズム探しに注力する愚は避けなければなりません。

問題

• (研究課題) 機械学習アルゴリズムは訓練データセットを 大きくする極限でどう振る舞うのでしょうか？どのようなアルゴリズムに対しても、 漸近的パフォーマンスの概念を大きな訓練データの極限で定義してみるのは自然なことです。 この問題に対する手っ取り早い方針としては、上に示したようなグラフを適当な近似曲線で フィッティングして、それを無限大まで外挿してみることです。このようなアプローチに 対しては、近似曲線の選び方によって異なる漸近的パフォーマンスにたどり着いてしまう という批判があるでしょう。特定の種類の近似曲線を使うことに対して、原理的な 正当化は可能ですか？もしそうなら、いくつかの異なる機械学習アルゴリズムに対して、 漸近的パフォーマンスの比較を行ってください。

まとめ： ここまで過適合と正規化について集中的に考察してきました。 これについては一旦ここでお終いにして次のトピックに移りますが、 これらの問題については再び戻ってくることになります。 何度も述べたように、コンピュータの性能が向上し、より大きなニューラルネットワークの 訓練が可能になるにつれ、ニューラルネットワークにおける過適合の問題も重要性を増しています。 結果として、過適合を軽減するより強力な正規化手法の開発が急務となっており、 現在も極めて活発な研究分野をなしています。

重みの初期化

ニューラルネットワークを学習させる前に、重みとバイアスの初期値を選ぶ必要があります。 これまでの例では、Chapter 1で 手短に議論した処方に従って選んできました。念のためもう一度書いておくと、 その処方とは、全ての重みとバイアスを平均 $0$、標準偏差 $1$ に規格化した独立なガウス分布に従って 選ぶものでした。これまではこの方法で上手くいきましたが、そのように選ぶべき根拠も 今のところ明らかではありません。重みとバイアスの初期値をより上手く選ぶことで、 ニューラルネットワークの学習を加速することはできないでしょうか？

実は、結論から言ってしまうと、規格化されたガウス分布を使うよりもずっと良い やり方があるのです。その理由を見るために、非常にたくさん、例えば $1,000$個の 入力ニューロンを持つニューラルネットワークを考えてみましょう。 そして、第1の隠れ層につながる重みを全て規格化されたガウス分布で初期化するとします。 しばらくは入力ニューロンと隠れ層の第1のニューロンを結ぶ重みに集中し、 ニューラルネットワークの残りの部分を無視することにします：

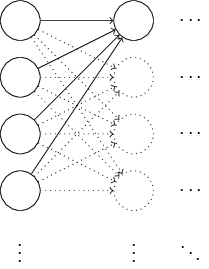
議論をさらに単純化するために、ある特定の訓練入力 $x$ を使って ニューラルネットワークを訓練することを考えます。その $x$ は、 半分の入力ニューロンがオン、すなわち $1$ の値を取り、残り半分のニューロンがオフ、 すなわち $0$ の値を取るものとします。以下の議論はより一般的な状況で成り立ちますが、 この特別な例から状況が大まかに理解できると思います。 隠れニューロンへの入力となる重み付き総和 $z = \sum_j w_j x_j+b$ を考えましょう。 半分の $x_j$ はゼロなので、総和のうち $500$ 項は消えます。 したがって、$z$ は $500$ 個の重みと $1$ 個のバイアスを合わせて、 全部で $501$ 個の規格化されたガウス分布変数の和になります。 したがって、$z$ 自身も平均がゼロで標準偏差が $\sqrt{501} \approx 22.4$ の ガウス分布に従うランダム変数です。 つまり、$z$ はかなり広がったガウス分布に従っていて、その分布は全く鋭くありません：

特に、$|z|$ が非常に大きく $z\gg 1$ か $z\ll -1$ が高い確率で成り立つことは、 このグラフから明らかです。その場合、隠れニューロンの出力 $\sigma(z)$ は $1$ か $0$ に非常に近い値を取ります。つまり、今考えている隠れニューロンは 飽和してしまうのです。そしてそうなってしまうと、重みを少し変化させても 隠れニューロンの活性はほんの僅かにしか変化しません。そしてこの非常に僅かな活性の変化は、 ニューラルネットワークの残りの部分に対してほとんど影響せず、最終的にコスト関数に ごく小さな変化しかもたらさないでしょう。結果として、これらの重みの学習に勾配降下法を使っても、 学習は非常にゆっくりとしか進行しないでしょう* *この点についてはより詳細にChapter 2で議論しました。その際、 逆伝播の式を 用いて、飽和したニューロンへ入力する重みの学習は遅くなることを示しました。。 この問題は、出力ニューロンが誤った値に飽和していると学習が非常に遅くなるという、 この章の前半で議論した問題と似ています。その際は、コスト関数を上手く選ぶことで その問題を解決しました。良いコスト関数は出力ニューロンの飽和の問題を解決しましたが、 残念ながら、同じ方法では隠れニューロンの飽和の問題は全く改善されません。

ここまで、第1の隠れ層に入力する重みについて議論してきました。もちろん、同様の議論は 他の隠れ層に対しても成り立ちます：隠れ層の重みを規格化されたガウス分布を使って 初期化した場合、隠れニューロンの活性はしばしば $0$ か $1$ に非常に近く、 学習は非常にゆっくりとしか進みません。

この種の飽和と学習の減速を避けるために、重みとバイアスのもっと上手い初期化の方法は あるのでしょうか？今、$n_{\rm in}$ 個の入力を持つニューロンを考えます。 その入力に掛かる重みを平均 $0$ で標準偏差 $1/\sqrt{n_{\rm in}}$ のガウス分布で 初期化しましょう。つまり、ガウス分布を押しつぶしてニューロンが飽和しづらくなるようにします。 バイアスについては後述する理由により、変わらず平均 $0$ で標準偏差 $1$ のガウス分布で初期化します。 そのように選ぶことで、重み付き総和 $z = \sum_j w_j x_j + b$ は再び平均 $0$ のガウス分布に 従うランダム変数となりますが、以前よりもずっと鋭い分布になります。 前に考えたように、$500$ 個の入力がゼロで $500$ 個の入力が $1$ だとしましょう。 このとき、簡単な計算により（下の演習参照）、$z$ は平均 $0$ で標準偏差 $\sqrt{3/2}=1.22\ldots$ のガウス分布に従うことが分かります。 この分布は前よりもずっと鋭いピークを持っています。実は、下のグラフではかなり控えめに ピークが描かれています。というのも、ピークの全体を描くために、このグラフでは前のグラフから 縦軸のスケールを変えているからです。

このようなニューロンはずっと飽和しづらく、学習の減速はずっと起こりづらいでしょう。

Exercise

• 上の段落に出てきた $z = \sum_j w_j x_j + b$ の標準偏差が $\sqrt{3/2}$ であることを 示してください。ヒント：(a) 独立なランダム変数の和の分散は、個々のランダム変数の分散の 和に等しくなります。(b) 分散は標準偏差の2乗です。

上述のように、バイアスについては以前と同様、平均が $0$ で標準偏差が $1$ のガウス分布で 初期化します。こうしてもニューロンの過剰に飽和させることは無いので大きな問題になりません。 実は、飽和の問題さえ避ければ、バイアスをどのように初期化しても大勢に影響はないのです。 全てのバイアスを $0$ に初期化して、あとは勾配降下法で学習するに任せる人さえ居ます。 どのように初期化しても大して変わりないので、私たちは以前と同じ方法でバイアスを初期化することにします。

では、MNISTの手書き文字分類のタスクを使って、重みの初期化のやり方による結果の違いを見てみましょう。 以前と同様に、$30$ 個の隠れニューロン、大きさ $10$ のミニバッチ、正規化パラメータ $\lambda=5.0$ と、 クロスエントロピーコスト関数を用いることにします。 結果をグラフ上で少し見やすくするため、学習率は $\eta=0.5$ から $0.1$ に少し減らすことにします。 まず、以前のやり方で重みを初期化してからニューラルネットワークを訓練してみましょう：

>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0,
... evaluation_data=validation_data,
... monitor_evaluation_accuracy=True)

>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0,
... evaluation_data=validation_data,
... monitor_evaluation_accuracy=True)

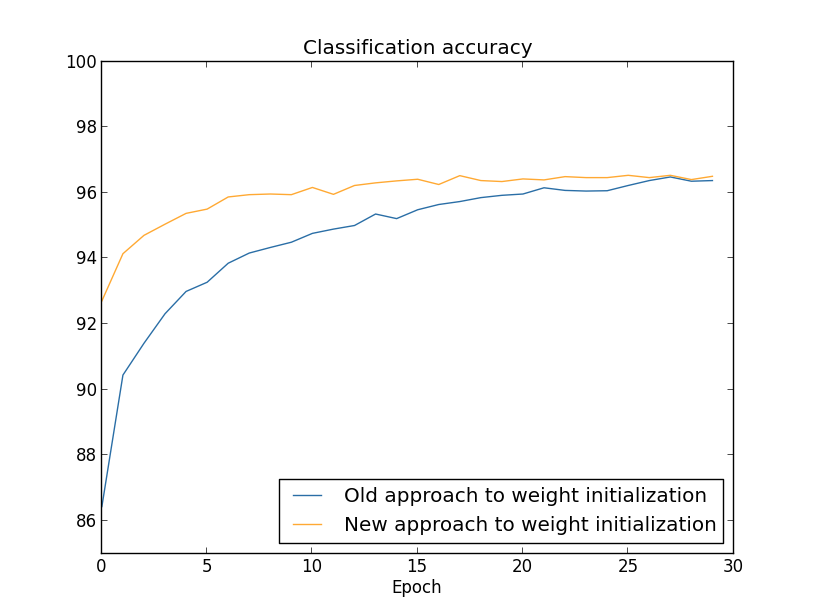
いずれの場合も、最終的な分類精度は96パーセント強といったところです。 30エポックで両者はほぼ同じ分類精度に到達します。しかし、新しい方法では、 ずっとずっと早くその分類精度に到達します。最初のエポックが終わったところで、 古いやり方では分類精度が87パーセント弱ですが、新しい方法では93パーセントに 達しようとしています。 重みの初期化方法を変えることで、古いやり方よりずっと良い領域から出発できて、 結果の改善もかなり素早く進行するのです。 同じ現象は $100$ 個の隠れニューロンを使っても起こります：

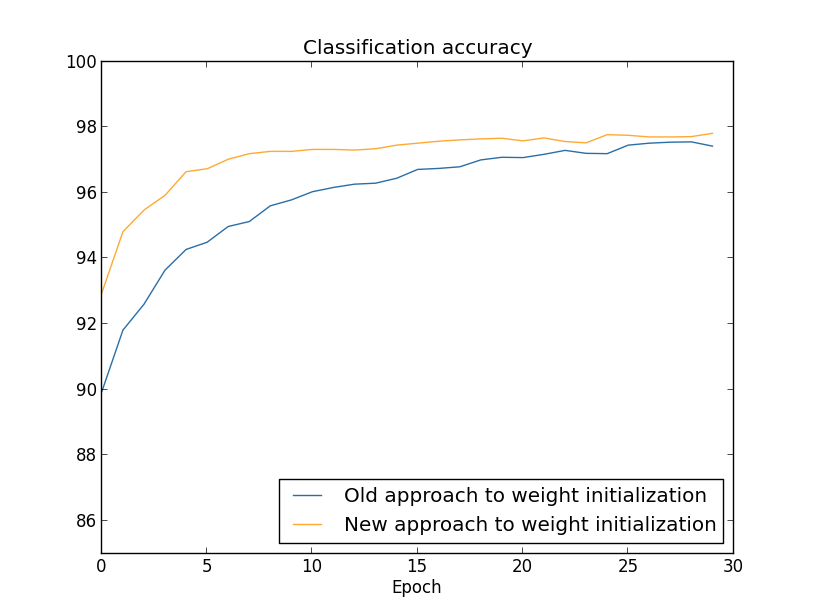
この場合には、2つの曲線が一致するには至っていません。しかし、私が自分で 実験してみた結果、あと2, 3エポックだけ訓練を続けると、分類精度はほとんど 同じになります。したがって、これらの実験の結果を見ると、重みの初期化方法を改善しても、 学習がスピードアップするだけで、最終的なニューラルネットワークのパフォーマンスを 改善することは無いかのように思えます。しかし、Chapter 4では、 重みの初期分布の標準偏差を $1/\sqrt{n_{\rm in}}$ にすることで、 ニューラルネットワークの長時間における振る舞いが顕著に改善される例を扱います。 重みの初期化方法は学習速度のみならず、 時にニューラルネットワークのパフォーマンスをも左右することになるのです。

重みの初期分布の標準偏差を $1/\sqrt{n_{\rm in}}$ にすることで、 ニューラルネットワークの学習が改善されます。重みを初期化する他の手法も 提案されていますが、多くは同じ基本的なアイデアに基づいています。 私たちの目的のためにはこれまでに紹介した方法で十分なので、ここでは他の手法は取り上げません。 関心がある読者は、Yoshua Bengioによる2012年の論文* *Practical Recommendations for Gradient-Based Training of Deep Architectures, by Yoshua Bengio (2012).の14, 15ページにある議論と、 そこで引用されている文献を見てみることを勧めます。

問題

• 正規化と改善された重み初期化法の関係 L2正規化することで、時々自動的に新しい方法で重みを初期化することと似た 効果が得られることがあります。重みの初期化に古い方法を使ったとしましょう。 ヒューリスティックな議論で次のことを示してください： (1) $\lambda$ が小さすぎなければ、訓練のはじめの数エポックでは重み減衰が支配的である。 (2) $\eta \lambda \ll n$ とすると、重みは $\exp(-\eta\lambda /m)$ の因子で減衰する。 (3) $\lambda$ が大きすぎないとすると、重みの多さが $1/\sqrt{n}$ になった辺りで、 重み減衰が落ち着いてくる。 ここで、$n$ はニューラルネットワークの全ての重みの数とします。 この節でグラフに示した例では、これら全ての条件が満たされていることを議論してください。

手書き文字認識再訪：コード

この章で議論してきたアイデアを実装しましょう。新しいプログラム network2.py を開発します。これはChapter 1で作成した network.py を修正したバージョンです。もし network.py の内容を覚えていなければ、 ここで軽く復習しておくと後の助けになるでしょう。たった74行のコードですし、 簡単に理解できます。

network.py と同様に、network2.py での中心選手も Network クラスです。 このクラスはニューラルネットワークを表しています。 Network のインスタンスを初期化するには、各層のニューロン数 sizes と コスト関数を指定する cost を指定します。コスト関数にはデフォルトでクロスエントロピー が指定されています：

class Network():

    def __init__(self, sizes, cost=CrossEntropyCost):
        self.num_layers = len(sizes)
        self.sizes = sizes
        self.default_weight_initializer()
        self.cost=cost

__init__ メソッド冒頭の2行は network.py と同じですし、 見れば何をしているのか分かるでしょう。しかし続く2行は新しく、 その挙動を詳細に理解する必要があります。

まずは default_weight_initializer を見てみましょう。 このメソッドでは改善された手法で重みを初期化します。 あるニューロンに入力する重みの数を $n_{\rm in}$ とすると、 新しい手法ではそのニューロンに入力する重みを平均 $0$ で標準偏差 $1/\sqrt{n_{\rm in}}$ の ガウス分布で初期化します。また、バイアスについては平均 $0$ で標準偏差が $1$ のガウス分布で 初期化します。そのコードは以下の通りです：

    def default_weight_initializer(self):
        self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
        self.weights = [np.random.randn(y, x)/np.sqrt(x)
                        for x, y in zip(self.sizes[:-1], self.sizes[1:])]

このコードを理解するために、まず np が線形代数計算を行う Numpy ライブラリーである ことを思い出しましょう。Numpy はプログラムの冒頭で import しています。 第1層は入力層なので、この層ではバイアスを初期化していません。 これは network.py で行ったことと同じです。

補足として、プログラムには large_weight_initializer メソッドも含まれています。 このメソッドは、重みとバイアスをChapter 1で使った古い方法、つまり平均 $0$ で標準偏差 $1$ の ガウス分布で初期化します。コードは、default_weight_initializer とほんの僅かに違うだけです：

    def large_weight_initializer(self):
        self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
        self.weights = [np.random.randn(y, x)
                        for x, y in zip(self.sizes[:-1], self.sizes[1:])]

large_weight_initializer メソッドを入れたのは、主にこの章の結果とChapter 1の 結果を簡単に比較できるようにするためです。 実際問題として古い方法を使うべき状況はほとんど思いつきません！

Network クラスの __init__ メソッドに関する第2の変更点は、 cost 属性を初期化する点です。この動作を理解するために、 クロスエントロピーコスト関数を表すクラスを見てみましょう* *もしPythonの静的メソッドに馴染みがなければ、@staticmethod デコレータは 気にせず、fn や delta を普通のメソッドだと考えて差し支えありません。 関心がある読者のために書いておくと、@staticmethod を付けることで、 そのメソッドはそれが属しているブジェクトに依存していないことを表しています。 fn や deltaメソッドが第1引数に self を受け取っていないのは そのためです。 ：

class CrossEntropyCost:

    @staticmethod
    def fn(a, y):
        return np.nan_to_num(np.sum(-y*np.log(a)-(1-y)*np.log(1-a)))

    @staticmethod
    def delta(z, a, y):
        return (a-y)

中身を詳しく見ていきましょう。まず気づいてほしいのは、クロスエントロピー自体は 数学的にいえば「関数」ですが、Pythonのクラスとして実装されている点です。 この実装を選んだのは、コスト関数がニューラルネットワークで2つの異なる役割を持つからです。 その1つ目は、出力活性 $a$ が正解の出力 $y$ にどのくらい似ているかの指標の役割です。 この役割は CrossEntropyCost.fn メソッドに実装されています。 （脇道に逸れますが、CrossEntropyCost.fn の中で呼ばれている np.nan_to_num は ゼロに非常に近い数値の対数をNumpyで正しく扱うために必要です。）もう一つの役割を 理解するために、Chapter 2で議論した逆伝播法を思い出しましょう。 逆伝播を行うには、ニューラルネットワークの出力誤差 $\delta^L$ を計算する必要があります。 そして、出力誤差の形は選んだコスト関数ごとに異なります。クロスエントロピーの場合、 出力誤差は式(66)\begin{eqnarray} \delta^L = a^L-y. \nonumber\end{eqnarray} で示した表式です：

\begin{eqnarray} \delta^L = a^L-y. \tag{92}\end{eqnarray} このため、第二のメソッド、CrossEntropyCost.delta を定義しました。 このメソッドは出力誤差を計算します。この2つは ニューラルネットワークがコスト関数について知るべきことの全てですから、 2つのメソッドを一つのクラスにまとめたのです。

同様に、network2.py は2乗コスト関数を表すクラスも含んでいます。 これはChapter 1の結果と比較するためだけに入っており、今後の議論ではほとんど クロスエントロピーのみを用います。コードは下に示しました。QuadraticCost.fn メソッドは 実際の出力 a と正解出力 y から2乗誤差を計算します。 QuadraticCost.delta から返される値は、Chapter 2で導出した2乗コスト関数の 出力誤差 (30)\begin{eqnarray} \delta^L = (a^L-y) \odot \sigma'(z^L) \nonumber\end{eqnarray} にもとづいています。

class QuadraticCost:

    @staticmethod
    def fn(a, y):
        return 0.5*np.linalg.norm(a-y)**2

    @staticmethod
    def delta(z, a, y):
        return (a-y) * sigmoid_prime_vec(z)

これで network2.py と network.py の主な違いは理解しました。 どれも簡単なことです。以下で議論するように、 L2正規化の実装など小さな変更点はたくさんあります。それらに取り掛かる前に、 network2.py の完全なコードを見てみましょう。 コード全体を細かく読んでいく必要はありません。その代わり、全体の構造を掴むようにしましょう。 特に、ドキュメント文字列を読むのはプログラムの各部が何をしているのか理解する 助けになるでしょう。もちろん、お望みなら深く掘り下げたら良いでしょう。 コードの読解に困ったら、下の文章を読んでからコードに戻ってても良いでしょう。 ともかく、まずはコードを示します：

"""network2.py
~~~~~~~~~~~~~~

An improved version of network.py, implementing the stochastic
gradient descent learning algorithm for a feedforward neural network.
Improvements include the addition of the cross-entropy cost function,
regularization, and better initialization of network weights.  Note
that I have focused on making the code simple, easily readable, and
easily modifiable.  It is not optimized, and omits many desirable
features.

"""

#### Libraries
# Standard library
import json
import random
import sys

# Third-party libraries
import numpy as np


#### Define the quadratic and cross-entropy cost functions

class QuadraticCost:

    @staticmethod
    def fn(a, y):
        """Return the cost associated with an output ``a`` and desired output
        ``y``.

        """
        return 0.5*np.linalg.norm(a-y)**2

    @staticmethod
    def delta(z, a, y):
        """Return the error delta from the output layer."""
        return (a-y) * sigmoid_prime_vec(z)


class CrossEntropyCost:

    @staticmethod
    def fn(a, y):
        """Return the cost associated with an output ``a`` and desired output
        ``y``.  Note that np.nan_to_num is used to ensure numerical
        stability.  In particular, if both ``a`` and ``y`` have a 1.0
        in the same slot, then the expression (1-y)*np.log(1-a)
        returns nan.  The np.nan_to_num ensures that that is converted
        to the correct value (0.0).

        """
        return np.nan_to_num(np.sum(-y*np.log(a)-(1-y)*np.log(1-a)))

    @staticmethod
    def delta(z, a, y):
        """Return the error delta from the output layer.  Note that the
        parameter ``z`` is not used by the method.  It is included in
        the method's parameters in order to make the interface
        consistent with the delta method for other cost classes.

        """
        return (a-y)


#### Main Network class
class Network():

    def __init__(self, sizes, cost=CrossEntropyCost):
        """The list ``sizes`` contains the number of neurons in the respective
        layers of the network.  For example, if the list was [2, 3, 1]
        then it would be a three-layer network, with the first layer
        containing 2 neurons, the second layer 3 neurons, and the
        third layer 1 neuron.  The biases and weights for the network
        are initialized randomly, using
        ``self.default_weight_initializer`` (see docstring for that
        method).

        """
        self.num_layers = len(sizes)
        self.sizes = sizes
        self.default_weight_initializer()
        self.cost=cost

    def default_weight_initializer(self):
        """Initialize each weight using a Gaussian distribution with mean 0
        and standard deviation 1 over the square root of the number of
        weights connecting to the same neuron.  Initialize the biases
        using a Gaussian distribution with mean 0 and standard
        deviation 1.

        Note that the first layer is assumed to be an input layer, and
        by convention we won't set any biases for those neurons, since
        biases are only ever used in computing the outputs from later
        layers.

        """
        self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
        self.weights = [np.random.randn(y, x)/np.sqrt(x)
                        for x, y in zip(self.sizes[:-1], self.sizes[1:])]

    def large_weight_initializer(self):
        """Initialize the weights using a Gaussian distribution with mean 0
        and standard deviation 1.  Initialize the biases using a
        Gaussian distribution with mean 0 and standard deviation 1.

        Note that the first layer is assumed to be an input layer, and
        by convention we won't set any biases for those neurons, since
        biases are only ever used in computing the outputs from later
        layers.

        This weight and bias initializer uses the same approach as in
        Chapter 1, and is included for purposes of comparison.  It
        will usually be better to use the default weight initializer
        instead.

        """
        self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
        self.weights = [np.random.randn(y, x)
                        for x, y in zip(self.sizes[:-1], self.sizes[1:])]

    def feedforward(self, a):
        """Return the output of the network if ``a`` is input."""
        for b, w in zip(self.biases, self.weights):
            a = sigmoid_vec(np.dot(w, a)+b)
        return a

    def SGD(self, training_data, epochs, mini_batch_size, eta,
            lmbda = 0.0,
            evaluation_data=None,
            monitor_evaluation_cost=False,
            monitor_evaluation_accuracy=False,
            monitor_training_cost=False,
            monitor_training_accuracy=False):
        """Train the neural network using mini-batch stochastic gradient
        descent.  The ``training_data`` is a list of tuples ``(x, y)``
        representing the training inputs and the desired outputs.  The
        other non-optional parameters are self-explanatory, as is the
        regularization parameter ``lmbda``.  The method also accepts
        ``evaluation_data``, usually either the validation or test
        data.  We can monitor the cost and accuracy on either the
        evaluation data or the training data, by setting the
        appropriate flags.  The method returns a tuple containing four
        lists: the (per-epoch) costs on the evaluation data, the
        accuracies on the evaluation data, the costs on the training
        data, and the accuracies on the training data.  All values are
        evaluated at the end of each training epoch.  So, for example,
        if we train for 30 epochs, then the first element of the tuple
        will be a 30-element list containing the cost on the
        evaluation data at the end of each epoch. Note that the lists
        are empty if the corresponding flag is not set.

        """
        if evaluation_data: n_data = len(evaluation_data)
        n = len(training_data)
        evaluation_cost, evaluation_accuracy = [], []
        training_cost, training_accuracy = [], []
        for j in xrange(epochs):
            random.shuffle(training_data)
            mini_batches = [
                training_data[k:k+mini_batch_size]
                for k in xrange(0, n, mini_batch_size)]
            for mini_batch in mini_batches:
                self.update_mini_batch(
                    mini_batch, eta, lmbda, len(training_data))
            print "Epoch %s training complete" % j
            if monitor_training_cost:
                cost = self.total_cost(training_data, lmbda)
                training_cost.append(cost)
                print "Cost on training data: {}".format(cost)
            if monitor_training_accuracy:
                accuracy = self.accuracy(training_data, convert=True)
                training_accuracy.append(accuracy)
                print "Accuracy on training data: {} / {}".format(
                    accuracy, n)
            if monitor_evaluation_cost:
                cost = self.total_cost(evaluation_data, lmbda, convert=True)
                evaluation_cost.append(cost)
                print "Cost on evaluation data: {}".format(cost)
            if monitor_evaluation_accuracy:
                accuracy = self.accuracy(evaluation_data)
                evaluation_accuracy.append(accuracy)
                print "Accuracy on evaluation data: {} / {}".format(
                    self.accuracy(evaluation_data), n_data)
            print
        return evaluation_cost, evaluation_accuracy, \
            training_cost, training_accuracy

    def update_mini_batch(self, mini_batch, eta, lmbda, n):
        """Update the network's weights and biases by applying gradient
        descent using backpropagation to a single mini batch.  The
        ``mini_batch`` is a list of tuples ``(x, y)``, ``eta`` is the
        learning rate, ``lmbda`` is the regularization parameter, and
        ``n`` is the total size of the training data set.

        """
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x, y in mini_batch:
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        self.weights = [(1-eta*(lmbda/n))*w-(eta/len(mini_batch))*nw
                        for w, nw in zip(self.weights, nabla_w)]
        self.biases = [b-(eta/len(mini_batch))*nb
                       for b, nb in zip(self.biases, nabla_b)]

    def backprop(self, x, y):
        """Return a tuple ``(nabla_b, nabla_w)`` representing the
        gradient for the cost function C_x.  ``nabla_b`` and
        ``nabla_w`` are layer-by-layer lists of numpy arrays, similar
        to ``self.biases`` and ``self.weights``."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # feedforward
        activation = x
        activations = [x] # list to store all the activations, layer by layer
        zs = [] # list to store all the z vectors, layer by layer
        for b, w in zip(self.biases, self.weights):
            z = np.dot(w, activation)+b
            zs.append(z)
            activation = sigmoid_vec(z)
            activations.append(activation)
        # backward pass
        delta = (self.cost).delta(zs[-1], activations[-1], y)
        nabla_b[-1] = delta
        nabla_w[-1] = np.dot(delta, activations[-2].transpose())
        # Note that the variable l in the loop below is used a little
        # differently to the notation in Chapter 2 of the book.  Here,
        # l = 1 means the last layer of neurons, l = 2 is the
        # second-last layer, and so on.  It's a renumbering of the
        # scheme in the book, used here to take advantage of the fact
        # that Python can use negative indices in lists.
        for l in xrange(2, self.num_layers):
            z = zs[-l]
            spv = sigmoid_prime_vec(z)
            delta = np.dot(self.weights[-l+1].transpose(), delta) * spv
            nabla_b[-l] = delta
            nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
        return (nabla_b, nabla_w)

    def accuracy(self, data, convert=False):
        """Return the number of inputs in ``data`` for which the neural
        network outputs the correct result. The neural network's
        output is assumed to be the index of whichever neuron in the
        final layer has the highest activation.  

        The flag ``convert`` should be set to False if the data set is
        validation or test data (the usual case), and to True if the
        data set is the training data. The need for this flag arises
        due to differences in the way the results ``y`` are
        represented in the different data sets.  In particular, it
        flags whether we need to convert between the different
        representations.  It may seem strange to use different
        representations for the different data sets.  Why not use the
        same representation for all three data sets?  It's done for
        efficiency reasons -- the program usually evaluates the cost
        on the training data and the accuracy on other data sets.
        These are different types of computations, and using different
        representations speeds things up.  More details on the
        representations can be found in
        mnist_loader.load_data_wrapper.

        """
        if convert:
            results = [(np.argmax(self.feedforward(x)), np.argmax(y))
                       for (x, y) in data]
        else:
            results = [(np.argmax(self.feedforward(x)), y)
                        for (x, y) in data]
        return sum(int(x == y) for (x, y) in results)

    def total_cost(self, data, lmbda, convert=False):
        """Return the total cost for the data set ``data``.  The flag
        ``convert`` should be set to False if the data set is the
        training data (the usual case), and to True if the data set is
        the validation or test data.  See comments on the similar (but
        reversed) convention for the ``accuracy`` method, above.
        """
        cost = 0.0
        for x, y in data:
            a = self.feedforward(x)
            if convert: y = vectorized_result(y)
            cost += self.cost.fn(a, y)/len(data)
        cost += 0.5*(lmbda/len(data))*sum(
            np.linalg.norm(w)**2 for w in self.weights)
        return cost

    def save(self, filename):
        """Save the neural network to the file ``filename``."""
        data = {"sizes": self.sizes,
                "weights": [w.tolist() for w in self.weights],
                "biases": [b.tolist() for b in self.biases],
                "cost": str(self.cost.__name__)}
        f = open(filename, "w")
        json.dump(data, f)
        f.close()

#### Loading a Network
def load(filename):
    """Load a neural network from the file ``filename``.  Returns an
    instance of Network.

    """
    f = open(filename, "r")
    data = json.load(f)
    f.close()
    cost = getattr(sys.modules[__name__], data["cost"])
    net = Network(data["sizes"], cost=cost)
    net.weights = [np.array(w) for w in data["weights"]]
    net.biases = [np.array(b) for b in data["biases"]]
    return net

#### Miscellaneous functions
def vectorized_result(j):
    """Return a 10-dimensional unit vector with a 1.0 in the j'th position
    and zeroes elsewhere.  This is used to convert a digit (0...9)
    into a corresponding desired output from the neural network.

    """
    e = np.zeros((10, 1))
    e[j] = 1.0
    return e

def sigmoid(z):
    """The sigmoid function."""
    return 1.0/(1.0+np.exp(-z))

sigmoid_vec = np.vectorize(sigmoid)

def sigmoid_prime(z):
    """Derivative of the sigmoid function."""
    return sigmoid(z)*(1-sigmoid(z))

sigmoid_prime_vec = np.vectorize(sigmoid_prime)

最も興味深い変更点の一つは、L2正規化を実装した点です。これは概念的には大きな変更ですが、 その実装はコードを読んでも見逃してしまうほど些細なことです。この点に関わる変更の大部分は、 様々なメソッド、特に Network.SGD に、パラメータ lmbda を渡すことです。 そして本質的な変更は1行のプログラム、Network.update_mini_batch メソッドの 終わりから4行目です。その部分で、重み減衰するように勾配降下法の更新規則を修正しています。 しかし、その修正はわずかでも、結果へは大きな影響を与えるのです！

ところで、このようなことはニューラルネットワークで新しい技術を実装する時に しばしば起こります。正規化を議論するのに大変長い文章を費やしました。 正規化は概念的にはとても微妙で理解するのも難しいものです。それでも、 プログラムに実装するのはとても簡単なことなのです。 洗練された高度な手法が、コードの僅かな変更で実装できてしまうことは、 驚くほど頻繁に起こります。

他の小さくても重要な変更点は、確率的勾配降下法を実行するメソッド Network.SGD に いくつかのオプションフラグを追加したことです。これらのフラグは、 training_data か evaluation_data でのコストと精度をモニターする ために用いられます。コストと精度を計算するデータ集合は Network.SGD に渡すことができます。 この章の中でもこれらのフラグを何度も使ってきましたが、思い出してもらうために、 今一度使い方の例を示しておきます：

>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost())
>>> net.SGD(training_data, 30, 10, 0.5,
... lmbda = 5.0,
... evaluation_data=validation_data,
... monitor_evaluation_accuracy=True,
... monitor_evaluation_cost=True,
... monitor_training_accuracy=True,
... monitor_training_cost=True)

ここでは、evaluation_data に validation_data をセットしていますが、 パフォーマンスのモニターには test_data を使うこともできますし、他のデータセットを使うこともできます。 その他に4つのフラグをセットして、コストと精度を evaluation_data と training_data の両方でモニターするよう設定しています。これらのフラグは デフォルトで False ですが、ここでは True にセットして Network のパフォーマンスをモニターしています。さらに、network2.py の Network.SGD メソッドは、モニタリングの結果を表す4要素のタプルを返します。 これは次のように利用します：

>>> evaluation_cost, evaluation_accuracy,
... training_cost, training_accuracy = net.SGD(training_data, 30, 10, 0.5,
... lmbda = 5.0,
... evaluation_data=validation_data,
... monitor_evaluation_accuracy=True,
... monitor_evaluation_cost=True,
... monitor_training_accuracy=True,
... monitor_training_cost=True)

ですから、例えば、evaluation_cost は30個の要素を持つリストで、 それぞれの要素は各エポック終了後の evaluation_data に対するコストです。 この種の情報はニューラルネットワークの振る舞いを理解する上で非常に有用です。 例えば、時間とともに学習が進行する様子をグラフに描く時に使えます。 実際、この章で示したグラフはこのようにして描いたものなのです。 ただし、もしモニタリングのフラグが設定されていなければ、 対応するタプルの要素は空リストになることに注意してください。

この他に追加した機能としては、Network オブジェクトをディスクに保存する Network.save メソッドと、保存した Network オブジェクトを 後から読み込む load 関数があります。 保存と読み込みは、Pythonで標準的に使われる pickle や cPickle ではなく、 JSONを使って行っています。JSONを使うほうが pickle や cPickle に比べて 多くのコードを必要とします。JSONを使った理由は、将来 Network クラスを修正する 可能性があるからです。例えば、シグモイドニューロンではなく他のニューロンを使うように Network を修正するとしましょう。この変更を実装するために、 Network.__init__ メソッドで定義する属性を変更することになるでしょう。 すると、単純に pickle を用いてしまうと load 関数は失敗してしまいます。 JSONを使いシリアル化を明示的に行うことで、 古い Network クラスをより簡単に確実に読み込むことができます。

他にも network2.py のコードにはたくさんの小さな変更があります。 しかし、それらは全て network.py からの単純な変化に過ぎません。 全体としては、74行のプログラムをより強力な152行に拡大する結果になりました。

問題

• 上のコードを修正して、L1正規化を実装してください。 また、30個の隠れニューロンを持つニューラルネットワークで、 L1正規化を使ってMNISTの手書き数字の分類を行ってください。 正規化を行わない場合よりも精度が良くなる正規化パラメータは見つかりますか？

• network.py の Network.cost_derivative メソッドを見てください。 このメソッドは2乗コスト関数用に書かれています。 これをクロスエントロピーコスト関数用に書き直すにはどうしたら良いでしょうか？ また、Network.cost_derivative メソッドのクロスエントロピー版で生じる問題を指摘してください。 network2.py では、Network.cost_derivative メソッドを完全に 無くしてしまい、代わりにその機能を CrossEntropyCost.delta メソッドに 実装しました。こうすることで、先に指摘した問題がどう解決されますか？

ニューラルネットワークのハイパーパラメータをどう選ぶか?

ここまでは、学習率 $\eta$ や正規化パラメータ $\lambda$ 等のハイパーパラメータを 私がどのように決めたのか説明せず、ニューラルネットワークが上手く働くよう私が 事前に決めた値を使ってきました。実際問題として、ニューラルネットワークを使って何かの 課題に取り組むにあたって、良いハイパーパラメータを見つけるのは困難な場合があります。 例えば、MNISTの手書き数字分類問題を今ここで初めて知って、 適切なハイパーパラメータの値を知らずにこれに取り掛かることを想像してみてください。 その際に最初の実験から、多くのハイパーパラメータについてこの章で使ってきた値、 30個の隠れニューロン、大きさ10のミニバッチ、そしてクロスエントロピーを使った30エポックの訓練を 運良く選んだとしましょう。しかし学習率については $\eta=10.0$、そして正規化パラメータは $\lambda = 1000.0$ を選んだとします。すると次のような結果が得られます：

>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10])
>>> net.SGD(training_data, 30, 10, 10.0, lmbda = 1000.0,
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)
Epoch 0 training complete
Accuracy on evaluation data: 1030 / 10000

Epoch 1 training complete
Accuracy on evaluation data: 990 / 10000

Epoch 2 training complete
Accuracy on evaluation data: 1009 / 10000

...

Epoch 27 training complete
Accuracy on evaluation data: 1009 / 10000

Epoch 28 training complete
Accuracy on evaluation data: 983 / 10000

Epoch 29 training complete
Accuracy on evaluation data: 967 / 10000

なんと分類精度は全くの当てずっぽうと同等です！ ニューラルネットワークはサイコロのようなものになってしまいました！

こんな風に考える読者がいるかもしれません。「ふむ、こんなのは簡単に直せるよ。 学習率と正規化ハイパーパラメータを小さくすれば良いんだろう」。 しかしちょっと待ってください。そう言えるのは上手く働くハイパーパラメータを 事前に知っていたからであって、学習率と正規化パラメータを調整すれば上手くいくことを ア・プリオリには知らないのです。もしかすると、隠れニューロンの数が30個では 他のハイパーパラメータをいかに調整しても上手くいかないのかもしれません。 もしかすると少なくとも100個、いや300個は隠れニューロンが必要なのでは？ あるいは隠れ層が複数必要なのでは？いや出力のエンコーディングが問題なのかもしれませんよ？ 本当は学習が進行しているけれども、もっと多くのエポックが必要という可能性はありませんか？ ミニバッチの大きさが小さすぎませんか？2乗コスト関数にしてみてはどうでしょう？ 重みの初期化方法を変えてみるのは？等など。広すぎるハイパーパラメータの空間で 途方に暮れてしまいそうです。巨大なニューラルネットワークを扱っていたり 巨大な訓練データを使ったりしている時には特に苛立たしい問題です。何しろ、 訓練するのに何時間も何日も、もしかすると何週間も掛かるのに、 何の結果も得られないこともあるのですから。 このような状況が続けば自信を無くすかもしれません。 もうこんな仕事は辞めて田舎で畑仕事でも始めたほうがマシに思えるかもしれません。

この節では、ニューラルネットワークのハイパーパラメータを定める発見的な方法を いくつか紹介します。目標は、ハイパーパラメータを上手に決めるためのワークフローを 読者が確立する手助けをすることです。もちろん、ハイパーパラメータの最適化について 全てをカバーするわけではありません。何しろとても大きな問題です。 そして、完全に解決されている問題ではないし、ニューラルネットワークを使う人々の間で 普遍的に共有されている合意も無いのです。 ニューラルネットワークのパフォーマンスをほんの少し向上させるために、 常に一つ、何かできることがあるはずです。この節で紹介する発見的な方法は、 その取っ掛かりを与えてくれるでしょう。

出発点： ニューラルネットワークを使って新しい問題に取り組む時、 第1の関門は何でも良いのでとにかく何か学習をすることです。 言い換えると、ニューラルネットワークでデタラメよりはマシな結果を達成することが第1歩です。 ものすごく低いハードルに思えるかもしれませんが、実際にはそれが驚くほど難しい場合もあります。 特に、新しい種類の問題に取り組む時には、この取っ掛かりから困難な場合があります。 まずはこの種の困難に遭った時に採りうる戦略を見てみましょう。

例えば、あなたがMNISTに初めて取り組むとしましょう。勢い勇んで取り掛かったものの、 ニューラルネットワークで得た最初の結果が先程見たような散々なもので、 少々落ち込んでいます。この状況を何とかするには、まず生じている問題を特定することです。 手始めに、訓練データと検証データから0と1以外の画像を全て取り除きましょう。 そして、ニューラルネットワークが0と1を区別できるように訓練してみましょう。 この0と1を区別するという新しい問題は、元々の10種類の数字を区別する問題より簡単であるのみならず、 訓練データの量を80%減らすことになるので、訓練が5倍速くなります。 こうすることで問題を特定するための実験を素早く実行することが可能になりますし、 良いニューラルネットワークを構築するにはどうしたら良いのか、素早い見立てが可能になります。

さらに素早く実験を行うには、まともに学習が可能であると期待できる範囲で、 ニューラルネットワークをできるだけ単純化することができます。 もし各層のニューロン数が [784, 10] のニューラルネットワークが MNISTの手書き数字分類問題に対して乱数よりはまともな正答率を達成できると考えるなら、 実験の出発点としてこのようなニューラルネットワークから実験を採用するのが良いでしょう。 ニューロン数が [784, 30, 10] のニューラルネットワークよりはずっと速く学習するでしょうから、 実験も速く進むでしょう。

実験をさらにスピードアップするには、モニタリングの頻度を上げるという方法があります。 network2.py では、訓練の各エポックが終了した時点でパフォーマンスを測定しました。 一つのエポックに50,000枚の画像が含まれるので、ニューラルネットワークの学習状況について 情報を得るのに随分と時間が掛かります。例えば、私のノートPCで各層のニューロン数が [784, 30, 10] のニューラルネットワークを訓練すると、 学習状況についてフィードバックを受けるまで約1分掛かります。 もちろん、1分というのは決して長時間ではありませんが、 大量のハイパーパラメータを決めたい時にはそれでも厄介です。 何百、何千通りものハイパーパラメータを試そうと思うと、随分と大きな負担です。 もっと頻繁に、例えば訓練画像1,000枚ごとに検証精度を監視することで、 より素早いフィードバックが得られます。さらに、 10,000枚の画像を全て使う代わりに100枚の検証画像から精度を推定することで、 より速くパフォーマンスを測定することが可能です。 大切なのは、まともな学習に必要なだけの訓練画像をニューラルネットワークに与えることと、 そこそこに良いパフォーマンスの推定を得ることなのです。もちろん、 network2.py は現時点でこういうモニタリングを行ってはいませんが、 ここでは実例として、MNISTの訓練データを1,000枚に減らしてみます。 動かしてみて何が起こるか見てみましょう。 (単純にするために、0と1の画像だけを使うというアイデアは実装していません。 もちろん、あと少し工夫すればそれを実装することも可能です。)

>>> net = network2.Network([784, 10])
>>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 1000.0, \
... evaluation_data=validation_data[:100], \
... monitor_evaluation_accuracy=True)
Epoch 0 training complete
Accuracy on evaluation data: 10 / 100

Epoch 1 training complete
Accuracy on evaluation data: 10 / 100

Epoch 2 training complete
Accuracy on evaluation data: 10 / 100
...

まだ出てくるのは純粋なノイズです！ でも一つ大きな進歩があります：今やフィードバックを得るのに1分も待つ必要がなく、 1秒毎に情報が得られます。これなら、ハイパーパラメータを変えて実験を繰り返すのも容易ですし、 あるいは様々な異なるハイパーパラメータをほぼ同時に試してみることさえも可能でしょう。

上の例では、$\lambda$ を以前に使った $\lambda = 1000.0$ のままにしておきました。 しかし、訓練データの数を変えたのだから、重み減衰の割合を一定に保つために $\lambda$ も 変更するべきです。この場合は、$\lambda = 20.0$ にすると前と重み減衰の因子が前と同じになります。 以下がその結果です：

>>> net = network2.Network([784, 10])
>>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 20.0, \
... evaluation_data=validation_data[:100], \
... monitor_evaluation_accuracy=True)
Epoch 0 training complete
Accuracy on evaluation data: 12 / 100

Epoch 1 training complete
Accuracy on evaluation data: 14 / 100

Epoch 2 training complete
Accuracy on evaluation data: 25 / 100

Epoch 3 training complete
Accuracy on evaluation data: 18 / 100
...

なんと、今度はシグナルが出ました！とても良い結果とは言えませんが、 ともかく偶然よりは良い結果です。 これは、さらなる改善を得るためにハイパーパラメータを修正していく際の出発点になります。 学習率をもっと大きくするべきだと推測するかもしれません。 （恐らく皆さんも気づいているように、これは愚かな推測です。 その理由についてはすぐに議論しますが、しばらくは我慢してください。） そこでその推測を検証するために、$\eta$ の値を $100.0$ まで上げてみましょう：

>>> net = network2.Network([784, 10])
>>> net.SGD(training_data[:1000], 30, 10, 100.0, lmbda = 20.0, \
... evaluation_data=validation_data[:100], \
... monitor_evaluation_accuracy=True)
Epoch 0 training complete
Accuracy on evaluation data: 10 / 100

Epoch 1 training complete
Accuracy on evaluation data: 10 / 100

Epoch 2 training complete
Accuracy on evaluation data: 10 / 100

Epoch 3 training complete
Accuracy on evaluation data: 10 / 100

...

これはひどい！この結果は、学習率が小さすぎるという推測が間違っていたことを示唆します。 そこで反対に、$\eta$ を $1.0$ まで小さくしてみましょう：

>>> net = network2.Network([784, 10])
>>> net.SGD(training_data[:1000], 30, 10, 1.0, lmbda = 20.0, \
... evaluation_data=validation_data[:100], \
... monitor_evaluation_accuracy=True)
Epoch 0 training complete
Accuracy on evaluation data: 62 / 100

Epoch 1 training complete
Accuracy on evaluation data: 42 / 100

Epoch 2 training complete
Accuracy on evaluation data: 43 / 100

Epoch 3 training complete
Accuracy on evaluation data: 61 / 100

...

こちらの方が良いですね！このように続けていって、ハイパーパラメータを一つずつ調整して、 パフォーマンスを徐々に改善していきます。学習率 $\eta$ の値を改善できたら、 次に正規化パラメータ $\lambda$ の改善に進みます。 それができたら、次はより複雑な構造のニューラルネットワーク、例えば隠れニューロンを10個持つ ニューラルネットワークで実験しましょう。前と同じように $\eta$ と $\lambda$ を調整します。 次に隠れニューロンを20個に増やして、他のハイパーパラメータも調整しましょう。 以下同様に、各段階で検証データの一部を使ったパフォーマンスの測定を行い、 その結果を参考にしながらより良いハイパーパラメータを見つけていきます。 これを続けていくうちに、しばしばハイパーパラメータを修正した効果が現れるのに 時間が掛かるようになるので、モニタリングの頻度を徐々に下げることができます。

これは一般的でとても有望な戦略に見えます。 しかし、実際のところ、上の議論でさえ見通しが楽観的すぎるのです。 何も学習しないニューラルネットワークをいじるのは、どうしようもなく骨の折れる作業です。 何日もハイパーパラメータの調整を行って、それでも無意味な結果しか得られないことだってあります。 ですから、改めて強調したいのですが、初期の段階では、実験をしたらできるだけ素早く フィードバックが得られるようにしておくことがとても重要なのです。 最初に問題やニューラルネットワークの構造を単純化してしまうと、 当初の目的から遠ざかってしまうように思えるかもしれません。 しかし、こうすることでニューラルネットワークが意味のある学習をするまでに掛かる時間はずっと短縮されるし、 一旦意味のあるシグナルが得られれば、ハイパーパラメータを調整することで ニューラルネットワークの性能はしばしば急速に向上していきます。 一番最初の取っ掛かりが、最も苦労するところなのです。

ここまでは一般的な話をしてきました。ここからは、ハイパーパラメータの決め方について、 私が勧める具体的な手順をいくつか見てみましょう。以下では、学習率 $\eta$、 L2正規化パラメータ $\lambda$、そしてミニバッチのサイズの決め方を議論します。 しかし、ここで述べることの多くは、 ニューラルネットワークのアーキテクチャや他の正規化法に関わるハイパーパラメータ、 あるいはモーメンタム係数などこの本で後に議論するハイパーパラメータ等にも当て余ります。

学習率： 3つの異なる学習率、$\eta = 0.025$、$\eta = 0.25$、$\eta = 2.5$ を 持つニューラルネットワークにMNISTの学習をさせることを考えます。他のハイパーパラメータについては、 以前に用いたのと同様、訓練は30エポック行い、ミニバッチのサイズは10、正規化パラメータは $\lambda = 5.0$ を採用します。また、ここでは $50,000$ 枚全ての訓練画像を用いることにします。 次のグラフは、訓練の経過とともにコストがどう変化するかを示しています* *このグラフは multiple_eta.pyを用いて生成したものです。：

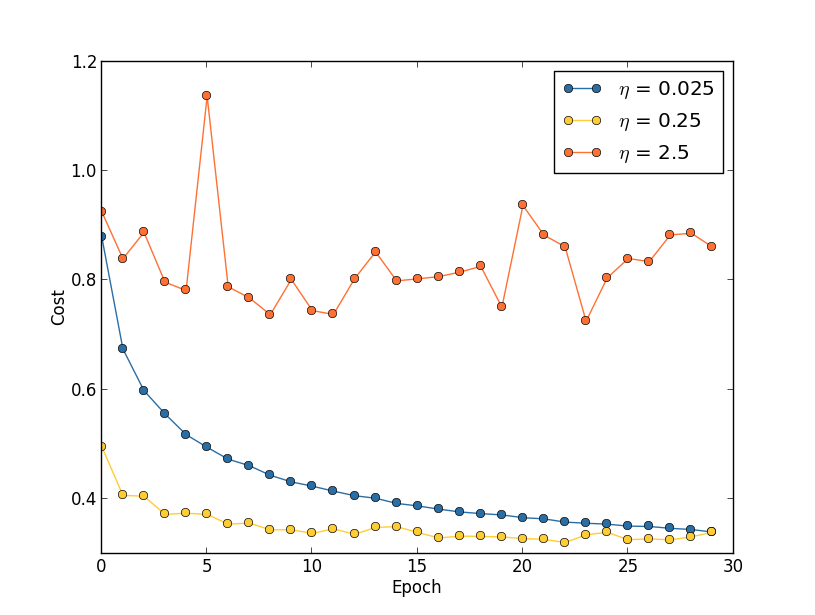
学習率 $\eta = 0.025$ では、最後のエポックまで滑らかにコストが減少しています。 $\eta = 0.25$ では、コストが最初減少しますが、20エポックを過ぎた辺りでほぼ飽和して、 その後はランダムに見える小さな振動をします。最後に、$\eta = 2.5$ では、 はじめからコストは大きな振動をしています。この振動が起こる理由を理解するために、 確率的勾配降下法ではコストの谷底に向かって小さなステップで 徐々に学習を進めていくことを思い出しましょう：

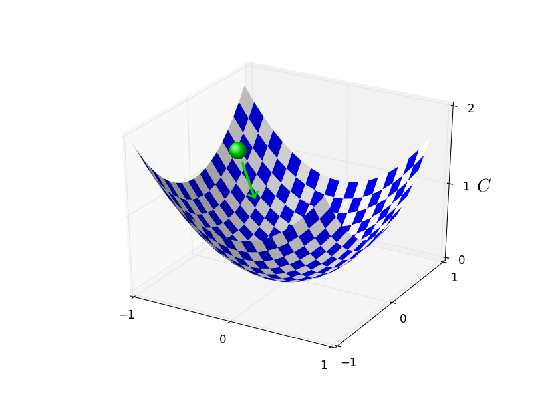
しかし、もし学習率 $\eta$ が大きすぎると、ステップが大きすぎてコストの最小を通り過ぎてしまう 可能性があります。そうすると、谷底に下る代わりに登ってしまうでしょう。 これが恐らく $\eta=2.5$ の時に起こっているのでしょう* *この描像は分かりやすいですが、あくまでも直感的な説明として示したもので、 完全な説明にはなっていません。より完全な説明は、手短に言うと次のようなものです： 勾配降下法では、コスト関数に対する一次近似を手がかりにコストを減少させようと試みます。 大きな $\eta$ では、コスト関数のより高次の項がより重要になり、 場合によってはコスト関数の振る舞いを決定づけるので、勾配降下法が破綻してしまいます。 これは特にコスト関数の最小や極小に近づくと起こりやすくなります。というのも、 そのような領域では勾配が小さくなり、高次の項が支配的になりやすくなるためです。。 $\eta=0.25$ の場合は、 最初しばらくはコスト関数の最小に向かって進み、最小に近づいた時だけ行き過ぎの問題が生じます。 $\eta=0.025$ を選ぶと、最初の30エポックでは同様の問題は一切生じません。もちろん、 これほど小さな学習率を選ぶと、確率的勾配降下法による学習が遅くなるという別の問題が生じます。 より良い方法は、$\eta=0.25$ から始めて20エポック訓練し、それから $\eta=0.025$ に切り替えることでしょう。 このように学習率を変動させる手法については後ほど議論します。 しばらくは、一つの良い学習率 $\eta$ をどう選ぶかについて考えましょう。

この描像を頭に入れておくと、$\eta$ を次のように定めることができます。 まず、コスト関数が振動や増加をせずちゃんと減少してくれる学習率の上限を見積もります。 この見積もりがとても正確である必要はありません。桁がわかれば良いという程度です。 ですから、$\eta=0.01$ から始めて数エポックの間コストが減少すれば、 順番に $\eta=0.1, 1.0, \ldots$ と試していき、コストが最初の数エポックで振動や増加を する値を見つけます。逆に、$\eta=0.01$ でも最初の数エポックでコストが振動や増加を始めたら、 $\eta=0.001, 0.0001, \ldots$ と試してい、コストが数エポックの間減少する値を見つけます。 これでコストを減少させられる学習率 $\eta$ の上限が大雑把に見積もられます。 もっと細かく、例えば $\eta=0.5$ や $\eta = 0.2$ のような値を試してみることで、 上限の見積もりを改善することも可能です（ただしこれが非常に正確である必要はありません）。

実際に使う $\eta$ の値はこの上限より小さく取らねばなりません。 実際のところ、選んだ学習率 $\eta$ が多くのエポックに渡って使い物になるためには、 例えば、上限の半分くらいに $\eta$ をとるのが良いかもしれません。 そのように選ぶことで、通常は学習の速度を落とし過ぎることなく、 より多くのエポックを使って訓練することが可能になります。

MNISTの場合には、この戦略に従うと、コストを減少させられる学習率の上限が 桁で言って $0.1$ 程度であるという見積もりを得ます。より細かく見ていくと、 $\eta=0.5$ 程度が上限であることが分かります。上記の処方に従うと、 学習率として $\eta=0.25$ を選ぶと良さそうだと言えます。 実際のところ、$\eta=0.5$ でも30エポックくらいなら十分に良く学習しますが、 たいていはより小さな $\eta$ を選んでも問題ありません。

ここで述べたことは、どれもとても単純に思えます。 しかし、$\eta$ を選ぶために訓練データに対するコスト関数の値を用いるのは、 この節で前に述べたことと矛盾するのではないでしょうか？つまり、ハイパーパラメータを選ぶには、 取っておいた("held-out")検証データを用いると言ったはずですよね？ 実際、正規化パラメータ、ミニバッチのサイズ、そして隠れ層や隠れニューロンの数など ニューラルネットワークのパラメータを定めるために、検証データに対する精度を用います。 では、学習率についてはなぜ状況が異なるのでしょうか？ 率直に言って、この選択は私の美的な好みによるもので、たぶん多少特殊ですが、 次のように理由付けできます。他のハイパーパラメータが試験データに対する最終的な分類精度の改善を 目的とするので、検証データに対する分類精度に基づいてチューニングするのは理にかなっています。 しかし、学習率が最終的な分類精度に与える影響は二義的なものです。 学習率をチューニングする一義的な目的は勾配降下法のステップ幅を制御することですから、 訓練データに対するコストを監視するのが大きすぎるステップ幅を検出する最良の方法であるはずです。 とは言え、あくまでもこれは私の個人的な美的趣味の問題です。 検証データに対する分類精度が改善するなら、学習の初期段階に訓練コストは減少するでしょうから、 実際上は検証データの分類精度と訓練コストのどちらを基準としても大した差は生じないと考えられます。

訓練エポック数を決める手段としての早期打ち切り： この章で前に議論したように、早期打ち切りとは各エポックが終了するたびに検証データに対する 分類精度を計算し、その改善が止まったら訓練を打ち切るという処方です。 こうすることで、とても簡単にエポック数を定めることができます。 この処方が特に便利なのは、訓練エポック数がその他のハイパーパラメータに対してどう依存するのか 気にする必要が無い点です。他のハイパーパラメータを変えると必要なエポック数も変わりますが、 その効果は自動的に取り込まれます。その上、早期打ち切りは自動的に過適合を防ぎます。 これはもちろん良いことです。 ただし、実験の初期の段階では、あえて早期打ち切りを行わない方が良い場合もあります。 早期打ち切りを止めることで過適合を起こし、その様子を調べることで正規化の指針を得るのです。

早期打ち切りを実装するには、まずは「分類精度の改善が止まる」という一文が意味するところを より正確に述べておく必要があります。既に見たように、分類精度が全体的に改善の傾向にあっても、 エポックを重ねるごとに改善し続けるわけではなく上がったり下がったりを繰り返すこともあります。 もし分類精度が始めて減少した時点で訓練をやめてしまうなら、 ほぼ間違いなく改善の余地を残してしまうことになるでしょう。 もっと良いやり方は、分類精度の最高値がしばらく更新されなかった時点で打ち切ることです。 例えば、MNISTの問題を考えましょう。そこで、分類精度が過去10エポックに渡って改善しなかった 時点で訓練を打ち切ることにするとどうでしょう。こうしておけば、訓練中の不運のために 早すぎる打ち切りを行ってしまうことは無いでしょうし、 全く改善の得られないまま永久に待ち続ける心配も無いでしょう。

この「10エポック・ルール」はMNIST問題の取っ掛かりに用いるには良いでしょう。 しかし、ニューラルネットワークでは時折、長期間に渡って分類精度が停滞した後に 再び改善を始める場合があります。もし本当に良いパフォーマンスを目指すなら、 10エポック・ルールでは忍耐が足りないかもしれません。 その場合の私の提案は、初期の実験で10エポック・ルールを採用し、 ニューラルネットワークの訓練状況が明らかになるに従い徐々に改善を待つ期間を長くしていくことです。 20エポック・ルール、50エポック・ルール、というように。 この戦略はもちろん、最適化の必要な新たなハイパーパラメータを生み出してしまいます！ しかし実際には、多くの場合このハイパーパラメータを決めるのは難しくありません。 MNIST以外の問題に対しても同様に、10エポック・ルールが早すぎるかそうでもないかは 問題の詳細に依存することですが、普通は少し実験をしてみれば早期打ち切りの良い戦略が 簡単に見つかるものです。

これまで示したコードでは、MNIST問題の実験で早期打ち切りを用いていません。 その理由は、多くの異なる学習手法を試して比較してきたからです。このような比較では、 それぞれの場合で同数のエポックを使うのが便利でしょう。 しかし、読者の皆さんは是非自分で network2.py を修正して早期打ち切りを実装してみてください：

問題

• network2.py を修正して「$n$エポック・ルール」を使った早期打ち切りを 実装してください。ここで、$n$ は指定できるパラメータとします。

• 「$n$エポック・ルール」以外に早期打ち切りの方法を挙げてみましょう。 理想的には、検証データに対する分類精度を上げることと訓練時間を短縮することを 上手くバランスさせるような規則であるべきです。そのような規則を network2.py に 追加した上で実験を3回行い、検証精度と訓練エポック数を10エポック・ルールと比較してください。

  学習率のスケジューリング： これまでは訓練の間、学習率 $\eta$ を定数に固定してきました。 しかし、しばしば学習率を変化させることが有効です。 学習過程の初期には、重みがひどく間違った値を取っているでしょうから、 大きな学習率を用いて学習の進みを早めるのが良いでしょう。その後、学習率を小さくしていくことで、 重みをより精密に調整することができます。

  学習率を訓練中に変更する具体的な手順、学習率のスケジューリングには、様々なものが考えられます。 一つの自然なアプローチは、早期打ち切りと同様の発想に基づくものです。 それは、まずは学習率を固定しておき、検証精度が悪くなり始めると、 学習率を例えば半分や10分の1程度に減らすというものです。 これを学習率が、例えば初期値の1,024分の1（あるいは1,000分の1）になるまで 繰り返してから学習を終了します。

  学習率のスケジューリングはパフォーマンスを改善しますが、 学習率のスケジューリングを決定するという新たな自由度をもたらします。 この選択が頭痛の種になりえます。学習率のスケジューリングを決めるために 無限の時間を掛けて試行錯誤することも可能でしょう。ですから、最初の実験に対する私の提案は、 ただ一つ、定数の学習率を用いることです。それで良い第1近似が得られるでしょう。 その後、ニューラルネットワークの発揮しうる最高のパフォーマンスを実現したいと考えるなら、 上で述べたような学習率のスケジューリングを試すと良いでしょう* *MNIST問題に取り組む際に学習率を変化させるご利益を示した最近の読みやすい論文として、 Deep, Big, Simple Neural Nets Excel on Handwritten Digit Recognition, by Dan Claudiu Cireșan, Ueli Meier, Luca Maria Gambardella, and Jürgen Schmidhuber (2010) を勧めます。。

  Exercise

  • network2.py を修正して、次のような学習率のスケジューリングを実装してください： 検証精度が10エポック・ルールを満たすごとに学習率を半分にし、学習率が初期値の $1/128$ に なった段階で訓練を終了させてください。

  正規化パラメータ $\lambda$： まずは正規化無し（$\lambda=0.0$）で、上述のように学習率 $\eta$ を最適化しましょう。 そこで決めた $\eta$ を使って、$\lambda$ の良い値を選びます。その時は、$\lambda=1.0$* *初期値として $\lambda=1.0$ を使うべき原理的な理由があるわけではありません。 $\lambda$ の探索をどこから始めるべきか、原理的な議論を知っている人がいたら、 教えていただけるとありがたく思います(mn@michaelnielsen.org)。 から 始めて、検証データに対する分類精度が改善するように $\lambda$ を10倍、あるいは10分の1倍していきます。 一旦 $\lambda$ の良い大きさがどのくらいの桁にあるのか分かったら、 さらに細かく $\lambda$ の値を調整しても良いでしょう。 それが終わったら、再び $\eta$ を最適化し直しましょう。

  演習

  • $\lambda$ や $\eta$ などのハイパーパラメータの良い値を決めるために、 勾配降下法を使いたくなるかもしれません。 勾配降下法を使った $\lambda$ の決定にはどのような障害があるでしょうか？ また、$\eta$ の決定に勾配降下法を使うことについてはどうでしょうか？

  私がこの本で使ったハイパーパラメータの選び方： この節で紹介してきた手順に従うと、この本でこれまで使ってきた $\eta$ や $\lambda$ の値と 必ずしも一致しない値が得られるでしょう。そうなる理由は、本書の中では説明の都合という制約のために、 いつも最適なハイパーパラメータを使うことができなかったためです。 これまで見てきた学習手法の比較を思い返してみましょう。 例えば、2乗コスト関数とクロスエントロピーコスト関数の比較、 重みの初期化に関する新旧2つのアプローチの比較、正規化の有無の比較、等など。 このような比較を意味あるものにするために、異なるアプローチで同じハイパーパラメータ （あるいは適切にスケールしたハイパーパラメータ）を使うように心掛けました。 当然、採用する学習手法によってハイパーパラメータの最適値は異なるのが普通です。 ですから、異なる手法を同じハイパーパラメータで比較するには、最適値をある程度諦めることになります。

  これに対する代案として、比較対象の手法のそれぞれでまず最適なハイパーパラメータの値を 求めておいて、最適な場合のパフォーマンス同士を比較するという方法も考えられます。 原理的には、こちらの方がより公平で良いアプローチかもしれません。 というのも、そうすることでそれぞれの手法の発揮しうる最高の性能を見ることができるからです。 しかし実際的には、様々な手法を取り上げ比較していく中で、計算量が多すぎるのです。 それが、私がこの本で部分的に最適なハイパーパラメータの使用を諦めた理由です。

  ミニバッチのサイズ： ミニバッチの大きさはどう決めるべきでしょうか？この問いに答えるために、 まずはオンライン学習、つまりミニバッチのサイズが $1$ の学習を考えましょう。

  まず心配になるのは、たった一つの訓練例しか含まないミニバッチでは、 推定した勾配が大きな誤差を持つのではないかということです。しかし実際のところ、 この誤差は大した問題でないことがわかります。 勾配の推定値が一つ一つ非常に正確である必要はないのです。 必要なのは、学習を進める間、コスト関数の減少傾向が続く程度の正確さです。 例えるなら、見るたびに10度か20度くらいズレる気まぐれなコンパスを持って北極を目指すようなものです。 コンパスが平均的には正しい方向を指して、しかも十分頻繁にコンパスを確認すれば、 最終的には北極にたどり着くことができるでしょう。

  この議論からは、オンライン学習がベストのように思えます。ところが実際には、 状況はもっと複雑です。前の章の問題では、 行列のテクニックを使うと、ミニバッチに含まれる訓練例に関するループを用いることなく、 ミニバッチ全体を使って一度に勾配の計算ができます。計算を行うハードウェアや 線形代数ライブラリの実装によっては、個別の訓練例を使った勾配計算を100回行うより、 100個の訓練例を含むミニバッチについて行列を使って勾配を計算した方がずっと早いことも あるのです。行列を使うと、1個の訓練例で勾配を計算するより、 例えば、100倍ではなく50倍しか時間が掛からないかもしれません。

  今の話は大して役に立たないと感じるかもしれません。 100個の訓練例を含むミニバッチを使って重みを学習する規則は次のようなものです： \begin{eqnarray} w \rightarrow w' = w-\eta \frac{1}{100} \sum_x \nabla C_x, \tag{93}\end{eqnarray} ここで、ミニバッチが含む訓練例に関する和を取っています。一方、オンライン学習では、 \begin{eqnarray} w \rightarrow w' = w-\eta \nabla C_x \tag{94}\end{eqnarray} となります。いくらミニバッチ更新に50倍の時間しか掛からないからと言っても、 まだオンライン学習の方が50倍頻繁に更新できるわけですから、 やはりオンライン学習の方が良いと結論してしまいそうです。しかしもし、 ミニバッチ学習の場合に学習率を100倍できるとしたらどうでしょう。 この場合、更新規則は次のように変わります： \begin{eqnarray} w \rightarrow w' = w-\eta \sum_x \nabla C_x. \tag{95}\end{eqnarray} こうなると、100個の個別の訓練例について、 学習率 $\eta$ でオンライン学習を行うのと同じに見えます。 しかも、1個の訓練例について学習するより50倍しか時間が掛からないのです。 もちろん、このミニバッチ学習はオンライン学習を100個の訓練例で実行するのと 全く同じというわけではありません。オンライン学習では個別の例を学習するごとに 重みを更新し、次の例では新しい重みを用いて勾配の計算を行うのに対して、 ミニバッチ学習では100個の訓練例について同じ重みを用いて計算を行うからです。 この点を考慮してもなお、ミニバッチ学習がオンライン学習よりも速い可能性は十分にあります。

  これらの要因を考慮すると、最適なミニバッチサイズはある種の妥協のもとで決まると言えます。 もし小さすぎれば、高速なハードウェアに最適化された行列ライブラリの恩恵を十分に受けられません。 もし大きすぎれば、重みの更新頻度が下がってしまいます。 やりたいのは、学習スピードを最大化するようなミニバッチサイズを決めることです。 幸い、学習スピードを最大化するミニバッチサイズは、ニューラルネットワークの アーキテクチャ以外のハイパーパラメータに対して比較的独立に決められるので、 良いミニバッチサイズを見つける前に予め他のハイパーパラメータを最適化しておく必要はありません。 ミニバッチサイズ以外のハイパーパラメータについては程よい値を入れておいて、 学習率 $\eta$ も上述のようにスケーリングしながら異なるミニバッチサイズを試してみれば良いのです。 そして、検証データに対する精度を時間についてプロットしましょう。 ここで、時間はエポック数ではなく、掛かった実時間であることに注意してください。 このプロットに基づいて、最もパフォーマンスの改善が速かったミニバッチサイズを 選べば良いのです。 他のハイパーパラメータの最適化は、ここで選んだミニバッチサイズを使って行います。

  もう気づいている読者も居るでしょうが、この本ではここに述べた最適化を行ってはいません。 実は、ここで述べたようなミニバッチ学習を高速化する手法を使ってさえいないのです。 これまでほとんど全ての具体例で、説明なしに大きさ10のミニバッチを用いてきました。 ですから、ミニバッチサイズを小さくすることで学習を高速化することもできたでしょう。 そうしなかった理由として、一つはミニバッチ更新のやり方を示したかったこと、 そしてもう一つは事前に行った実験からミニバッチサイズを小さくしても大して 学習速度は改善しないと考えられたことが挙げられます。 しかし実際の実装では、ほぼ間違いなくミニバッチ更新を高速な行列ライブラリ等を用いて実装し、 全体の学習スピードを最大化するようにミニバッチサイズの最適化も行うでしょう。

  自動化技術： ここまでは、ハイパーパラメータの最適化を手で行うかのように説明してきました。 自分の手を動かして最適化を行うことは、ニューラルネットワークの振る舞いについて 感覚を養うのに良い方法です。 しかし、当然ながら、実際は多くの場合にこの過程は自動化されています。 よく使われるのはグリッド探索という方法で、ハイパーパラメータの空間を グリッド状に系統的に探索します。 グリッド探索の成果と限界（そして簡単に実装できる代替手法）に関するレビューとして、 James BergstraとYoshua Bengioによる2012年の論文* *Random search for hyper-parameter optimization, by James Bergstra and Yoshua Bengio (2012).を挙げておきます。 より洗練された手法も多数提案されています。ここでそれらの全ては紹介しませんが、 ベイズ統計に基づくハイパーパラメータの自動最適化を用いた2012年の論文は 特に有望と思われるので紹介しておきます* *Practical Bayesian optimization of machine learning algorithms, by Jasper Snoek, Hugo Larochelle, and Ryan Adams.。 この論文のコードは公開されており、 他の研究者にも利用されいくつかの成功を収めています。

  まとめ： ここで大雑把に説明してきたやり方に従っても、ニューラルネットワークが持つ最大限の性能を 発揮できることが保証されているわけではありません。とは言え、さらなる改善を前に 十分良い出発点に立つことはできるはずです。特に、ここでの説明はハイパーパラメータごとに ほぼ独立して行ってきましたが、実際にはハイパーパラメータ同士の関係も問題になります。 例えば、まず $\eta$ の最適化を行ってから $\lambda$ の最適化に取り掛かると、 $\eta$ が再び最適からは程遠い状態になってしまう、なんてことも起こりえます。 実際上は、両者を行ったり来たりしながら徐々に良い値に近づいていくのが上手いやり方です。 そして何より、ここまで説明してきたことはあくまで経験則であって、 金科玉条の類ではないことを心に留めておいてください。 ここに書いたやり方に従っているときも、常に上手くいっていないところが無いか気を配り、 その兆しがあれば自分で実験してみることが大切です。 これは、ニューラルネットワークの振る舞い、特に検証精度を注意深くチェックすることを意味します。

  さらに厄介なのは、ハイパーパラメータの選び方のコツがあらゆるところに散らばっている点です。 たくさんの研究論文やプログラムの中に散らばっていますし、個々の技術者の頭の中にしか無いコツも 少なくありません。本当にたくさんの論文が様々な（そして時に互いに矛盾する）方法を勧めています。 しかし、中には僅かながら特に役立つ論文があり、雑多な情報の中からエッセンスをまとめてくれています。 Yoshua Bengioによる2012年の論文* *Practical recommendations for gradient-based training of deep architectures, by Yoshua Bengio (2012).には、逆伝播法や勾配降下法を用いた （多層）ニューラルネットワークの学習について実践的なアドバイスが記されています。 Benigoは、より系統的なハイパーパラメータの決め方など、多くの事項について この本よりもずっと詳細に議論しています。他におすすめしたい論文は、Yann LeCun, Léon Bottou, Genevieve Orr, そしてKlaus-Robert Müllerによる1998年の論文* *Efficient BackProp, by Yann LeCun, Léon Bottou, Genevieve Orr and Klaus-Robert Müller (1998)です。 どちらの論文も、ニューラルネットワークで用いられる様々な技法を集めた、 非常に有用な2012年の本* *Neural Networks: Tricks of the Trade, edited by Grégoire Montavon, Geneviève Orr, and Klaus-Robert Müller.に収められています。 この本は高価ですが、恐らく出版社のご厚意で、多くの論文は各著者のウェブサイトで公開されており、 検索エンジンを使って探し出せます。

  これらの文献を読んで、自分自身でも実験を行ってみると、ハイパーパラメータの最適化は 完全解決のない試みであることがはっきりしてくるでしょう。 ある手法を試みれば、そのパフォーマンスを改善できる別の手法が常に見つかるものです。 作家の間には、執筆は決して終わることは無く、ただ放り出してしまうだけなのだ、という格言があります。 ニューラルネットワークの最適化についても同じことが言えます：ハイパーパラメータの空間は あまりに広いので最適化に終わりはなく、どこかで放り出してしまうしか無いのです。 ですから、十分に良い最適化を手際よく行う作業工程を確立し、 必要なときにだけより詳細な最適化を行う柔軟性を残すことを目指すべきです。

  ニューラルネットワークを他の機械学習手法と比較して、 ハイパーパラメータを決めることの困難について文句を言う人も居ます。 例えば、おおよそ次のような文句はたくさん聞きました：「確かに、良くチューニングされた ニューラルネットワークはこの問題に対して最高のパフォーマンスを発揮するかもしれない。 一方で、ランダムフォレストを（あるいはSVMを、あるいは$\ldots$、何でも好きな手法を入れてください） 試してみることもできる。そしてその手法でも上手く行くだろう。 ニューラルネットワークに取り組んでいる時間なんて無いよ。」もちろん、実用上は 簡単に利用できる技術があるのは良いことです。何か新しい問題に取り掛かる時、 そして機械学習が役に立つかさえ明らかでは無いような状況では、特にそう言えます。 一方で、最適なパフォーマンスを得ることが重要なら、より高度な知識を必要とするアプローチを 試してみることも必要でしょう。機械学習がいつでも簡単に使えるなら嬉しい限りですが、 そのように期待すべきア・プリオリな理由もないのです。

  その他の手法

  この章で開発したさまざまな手法は、それ自身知っておく価値があるものたちばかりです。 しかし、私がそれらの手法を説明したのは、単にそれ自体の価値のためだけではありません。 ニューラルネットワークを扱う上で起こりうる問題や、それを克服する助けとなる解析のスタイルについて、皆様にも慣れていただく、 というのが、より重要な目標でした。 ある意味では、私たちはニューラルネットについて考える方法を学習していたのです。 この章の残りでは、これまでにカバーしきれなかった他の手法を軽く紹介します。 これからの紹介は、これまでの議論よりは深みに欠けるものになってしまいますが、 ニューラルネットワークを扱う手法の多様さを感じていただければ幸いです。

  確率的勾配降下法のバリエーション

  逆伝播法による確率的勾配降下法はMNIST手書き数字分類問題に対して十分な働きをしてきました。 しかし、コスト関数の最適化については他にも多くのアプローチがあり、 時にはそれらの手法がミニバッチを使った確率的勾配降下法よりも優れた性能を発揮する場合もあります。 この節ではヘッセ行列法とモメンタム法の2つを概観します。

  ヘッセ行列法： この手法について議論する上で、 ひとまずニューラルネットワークのことは脇においておきましょう。その代わり、 多変数 $w=w_1, w_2, \ldots$ のあるコスト関数 $C(w)$ を最小化するという抽象的な問題を考えましょう。 テイラーの定理により、コスト関数は点 $w$ の周りで \begin{eqnarray} C(w+\Delta w) & = & C(w) + \sum_j \frac{\partial C}{\partial w_j} \Delta w_j \nonumber \\ & & + \frac{1}{2} \sum_{jk} \Delta w_j \frac{\partial^2 C}{\partial w_j \partial w_k} \Delta w_k + \ldots \tag{96}\end{eqnarray} と近似できます。これをよりコンパクトに、 \begin{eqnarray} C(w+\Delta w) = C(w) + \nabla C \cdot \Delta w + \frac{1}{2} \Delta w^T H \Delta w + \ldots, \tag{97}\end{eqnarray} と書き換えることもできます。ここで、$\nabla C$ はコスト関数の勾配、 $H$ はヘッセ行列と呼ばれる行列で、その $j$ 行 $k$ 列の要素は $\partial^2 C/\partial w_j \partial w_k$ です。上で省略した高次の項を無視すると、 次の近似式が得られます：\begin{eqnarray} C(w+\Delta w) \approx C(w) + \nabla C \cdot \Delta w + \frac{1}{2} \Delta w^T H \Delta w. \tag{98}\end{eqnarray} 簡単な計算により、この右辺を最小化するには* *厳密に言うと、これが極小ではなく最小であるためには、ヘッセ行列が正定値である必要があります。 直感的には、$C$ が局所的に山や鞍点ではなく谷になっていることを意味します。 \begin{eqnarray} \Delta w = -H^{-1} \nabla C. \tag{99}\end{eqnarray} と選べば良いことが分かります。 式 (98)\begin{eqnarray} C(w+\Delta w) \approx C(w) + \nabla C \cdot \Delta w + \frac{1}{2} \Delta w^T H \Delta w \nonumber\end{eqnarray} が 良い近似であるとすると、点 $w$ から $w+\Delta w = w-H^{-1} \nabla C$ へ移動することで コスト関数を大きく減少させられると期待できます。このことから、 次のようなコスト関数の最小化アルゴリズムが考えられます：

  • 出発点 $w$ を選びます。

  • 点 $w$ を新しい点 $w' = w-H^{-1} \nabla C$ に更新します。ここで、$\nabla C$ と ヘッセ行列 $H$ は点 $w$ で計算します。

  • 点 $w'$ を新しい点 $w{'}{'} = w'-H'^{-1} \nabla' C$ に更新します。ここで、 ヘッセ行列 $H'$ と $\nabla' C$ は点 $w'$ で計算します。

  • $\ldots$
  実際には、式 (98)\begin{eqnarray} C(w+\Delta w) \approx C(w) + \nabla C \cdot \Delta w + \frac{1}{2} \Delta w^T H \Delta w \nonumber\end{eqnarray} はあくまで近似であり、 更新はもっと小さい幅で行うべきです。そのためには、学習率 $\eta$ を導入し、 $w$ の変化量を $\Delta w = -\eta H^{-1} \nabla C$ にすれば良いです。

  コスト関数を最小化するこのアプローチは ヘッセ行列法 あるいは ヘッセ行列最適化 と呼ばれます。ヘッセ行列法が標準的な勾配降下法と比べて少ないステップ数で収束することが 理論的・経験的に知られています。特に、コスト関数の2次の変化を取り入れることで、 勾配降下法について知られている多くの病的な振る舞いを避けられることが知られています。 さらに、ヘッセ行列を計算するために拡張された逆伝播法も知られています。

  ヘッセ行列最適化がそんなに素晴らしいのなら、なぜこれまで見てきたニューラルネットワークで 使っていないのでしょうか？確かにヘッセ行列法は多くの良い性質を持ってはいるものの、 一つ重要な、非常に好ましくない性質も持っています：ヘッセ行列は非常に大きいのです。 例えば、重みとバイアスを合わせて $10^7$ 個のパラメータを持つニューラルネットワークを 訓練するとします。すると、そのヘッセ行列は $10^7\times10^7 = 10^{14}$ 個もの要素を持ちます。 この大量にある要素を計算しなければならないのみならず、逆行列まで計算しなければならないのです！ このため、ヘッセ行列法を実際に適用するのは難しいのです。 しかし、この方法には理解しやすいというメリットもあります。実は、 勾配降下法の亜種には、ヘッセ行列法に触発された、しかし巨大な行列の問題を伴わない手法が 数多く有ります。次に、そのような手法の一つ、モメンタム勾配降下法を見てみましょう。

  モメンタム勾配降下法： 直感的に、ヘッセ行列法の強みは勾配の情報に加えて勾配の変化に関する情報を 取り入れられる点にあると言えます。モメンタム勾配降下法は同様の直感に基づいていますが、 2階微分の巨大な行列を取り扱うことを巧妙に回避しています。 モメンタム法を理解するために、以前に示した勾配降下法の 直感的な描像に戻って、 谷を転がり落ちるボールを考えてみましょう。勾配降下法はその名前の割に、 実際にはそれほど谷底に落ちていくボールと似ていないことは既に指摘しました。 モメンタム法では、2つの点で勾配加工法を修正し、より物理的な描像と近づけています。 第一に、この手法では最適化するパラメータに「速度」の概念を導入します。 勾配はこの速度を変化させますが、「位置」を（直接的には）変化させません。 これは、物理的な「力」は速度を変化させますが、位置の変化は速度の変化を介して間接的にしか 引き起こさないことと似ています。第2に、モメンタム法ではある種の摩擦項を導入し、 自然と徐々に減速するように仕向けます。

  より精密で数学的な説明をしましょう。それぞれのパラメータ変数 $w_j$ に対して、 速度変数 $v=v_1, v_2, \ldots$ を導入します* *もちろん、ニューラルネットワークの$w_j$ 変数は全ての重みとバイアスを含みます。。 そして、勾配降下法におけるパラメータの更新規則を $w \rightarrow w'= w-\eta \nabla C$ から \begin{eqnarray} v & \rightarrow & v' = \mu v - \eta \nabla C \tag{100}\\ w & \rightarrow & w' = w+v' \tag{101}\end{eqnarray} に置き換えます。ここで、$\mu$ は系の減衰、あるいは摩擦の大きさを決めるハイパーパラメータです。 この方程式の意味を理解するには、まず摩擦が無い場合に相当する $\mu=1$ を考えてみるのが良いでしょう。 その場合、$\nabla C$ が「力」として速度 $v$ を変化させること、 そして速度が $w$ の変化率を与えていることが見て取れます。 直感的には、勾配項を繰り返し足し上げることで速度が生じます。 学習の数ステップに渡って勾配が（大まかに）同じ方向ならば、 その方向にかなりの勢いがつきます。 例えば、下り坂を真っ直ぐ下る時に何が起こるか考えてみてください：

  

  ステップ毎にスロープを下る速度が増していき、加速しながら谷底まで素早く移動していきます。 これがモメンタム法が通常の勾配降下法よりも高速に学習する仕組みです。 もちろん、このままでは谷底を通り過ぎてしまう問題が有ります。 また、勾配が素早く変化する場合には、間違った方向に進んでしまうこともあるでしょう。 この問題を解決するために、$\mu$ というハイパーパラメータを式 (100)\begin{eqnarray} v & \rightarrow & v' = \mu v - \eta \nabla C \nonumber\end{eqnarray} に導入したのです。 既に、$\mu$ が摩擦を表すハイパーパラメータであるという説明をしました。より正確に言えば、 $1-\mu$ が摩擦の大きさを表しています。既に見たように、$\mu=1$ の時には摩擦が無く、 $\nabla C$ が加速度の役割をして速度を変化させます。反対に、$\mu=0$ の場合には、 摩擦が大きて加速がつかず、式 (100)\begin{eqnarray} v & \rightarrow & v' = \mu v - \eta \nabla C \nonumber\end{eqnarray} と (101)\begin{eqnarray} w & \rightarrow & w' = w+v' \nonumber\end{eqnarray} は元の勾配下降法 $w \rightarrow w'=w-\eta \nabla C$ に帰着します。実用的には、$\mu$ を0と1の間に取ることで、 谷底を行き過ぎること無く、学習を加速することが可能になります。 検証データを用いると、$\eta$ や $\lambda$ を決定したのと同じように $\mu$ の値を決定できます。

  ここまで、ハイパーパラメータ $\mu$ に名前を付けるのを避けてきました。 その理由は、$\mu$ の標準的な名前があまりに酷いからです：モメンタム係数 と呼ばれています。この名前は混乱の元になると思います。というのも、 $\mu$ は物理におけるモメンタムの概念とは全く何の関係も無いからです。 むしろ、摩擦と非常に関係があります。しかし、モメンタム係数という言葉は広く使われているので、 今後はこの言葉を使うことにします。

  モメンタム法の優れた点は、元の勾配降下法の実装を修正してモメンタムの効果を取り入れるのが 非常に容易であることです。以前と全く同じように逆伝播法を使って勾配を計算できますし、 ミニバッチを使った確率的サンプリングの考えも同じように適用できます。 このように、勾配の変化の情報を使うことでヘッセ行列法の利点を部分的に活用できます。 しかも、ほとんどデメリットが無く、少しだけ実装を修正するだけで良いのです。 実際の現場でもモメンタム法は広く利用され、学習の加速に貢献しています。

  演習

  • もしモメンタム法で $\mu>1$ とするとどのような問題が起こるでしょうか？

  • もし $\mu < 0$ とするとどのような問題が起こるでしょうか？

  問題

  • モメンタム法に基づいた確率的勾配降下法を network2.py に追加してください。

  コスト関数を最小化するその他の手法： コスト関数を最小化する手法はこの他にも多数開発されてきましたが、どれが最適な手法か という問いに対しては一致した回答がありません。ニューラルネットワークを使い込んでいく中で、 他の手法に取り組み、その挙動や利点・欠点を理解することは役に立つでしょう。 前に示した論文* *Efficient BackProp, by Yann LeCun, Léon Bottou, Genevieve Orr and Klaus-Robert Müller (1998).では、 共役勾配降下法やBFGS法（これと非常に関係の深い、 L-BFGS法と呼ばれる 記憶制限BFGS法も重要です）を含め、幾つかの方法が紹介・比較されています。 他に最近優れた結果* *例えば、次の論文を参照してください。 On the importance of initialization and momentum in deep learning, by Ilya Sutskever, James Martens, George Dahl, and Geoffrey Hinton (2012).を出した手法としては、モメンタム法を修正したNesterovによる加速勾配法があります。 しかし、多くの問題に対して、単純な確率的勾配降下法も、特にモメンタム法と組み合わせた時には 良い性能を発揮します。ですから、この本の残りの部分では確率的勾配降下法を使うことにします。

  人工ニューロンのその他のモデル

  ここまでは、シグモイドニューロンを使ってニューラルネットワークを組み立ててきました。 原理的には、シグモイドニューロンから成るニューラルネットワークは任意の関数を計算できます。 しかし現実的には、他のニューロンモデルを使ったニューラルネットワークが シグモイドニューラルネットワークよりも高性能になる場合もあります。 応用先によっては、そのような別のモデルに基づいたニューラルネットワークの方が 速く学習したり試験データに対してより良い汎化性能を発揮したりします。 ここでは、シグモイドニューロン以外のモデルを幾つか紹介します。

  恐らく最も単純なのは、tanhニューロンでしょう。これは、ニューロンのシグモイド関数を 双曲線正接関数に置き換えたものです。入力 $x$、重み $w$、バイアス $b$ の時、tanhニューロンの出力は \begin{eqnarray} \tanh(w \cdot x+b) \tag{102}\end{eqnarray} で与えられます。ここで、$\tanh$ はもちろん双曲線正接関数です。 実は、シグモイドニューロンとは非常に関係しています。$\tanh$ 関数の定義 \begin{eqnarray} \tanh(z) \equiv \frac{e^z-e^{-z}}{e^z+e^{-z}}. \tag{103}\end{eqnarray} を思い出すと、簡単な計算で \begin{eqnarray} \sigma(z) = \frac{1+\tanh(z/2)}{2} \tag{104}\end{eqnarray} という関係が示せます。つまり、$\tanh$ はシグモイド関数をリスケールしただけなのです。 グラフを描いてみても、$\tanh$ 関数のグラフがシグモイド関数と同じ形をしていることが分かります。

  tanhニューロンとシグモイドニューロンの違いの一つは、tanhニューロンの出力の値域が -1から1である点です。このため、tanhニューロンを使ってニューラルネットワークを構築する際には、 シグモイドニューロンを使った時とは少し違った方法で出力を規格化する必要があります。 この規格化の選択は、場合によっては解くべき問題の詳細や入力にも依存するでしょう。

  シグモイドニューロンの場合と同様に、tanhニューロンのネットワークも原理的には、 入力を-1から1に写す任意の関数を計算できます* *細かいことを言えば、どのような種類のニューロンを用いるにせよ、 この主張を正しく理解するためには少々技術的な注意が必要です。 しかし、大雑把に言えばニューラルネットワークが任意の関数を任意の精度で近似できる と考えて差し支えありません。。さらに、逆伝播法や確率的勾配降下法を tanhニューロンのネットワークに移植することも容易に可能です。

  演習

  • 式 (104)\begin{eqnarray} \sigma(z) = \frac{1+\tanh(z/2)}{2} \nonumber\end{eqnarray} の等号 を示してください。

  tanhとシグモイド、どちらのニューロンを使うべきなのでしょうか？穏やかに言えば、 ア・プリオリには明らかな答えはありません。しかし、時としてtanhの方が 高い性能を発揮できることを示唆する理論的な議論や経験的な証拠があります * *参考文献としては、例えば、 Efficient BackProp, by Yann LeCun, Léon Bottou, Genevieve Orr and Klaus-Robert Müller (1998), そして Understanding the difficulty of training deep feedforward networks, by Xavier Glorot and Yoshua Bengio (2010) をご覧ください。。 理論的な議論とはどういうものか感じてもらうために、 その内容を手短に紹介します。シグモイドニューロンを使っていて、 ニューラルネットワーク中の全ての活性が正の値を取るとしましょう。そして、 第$l+1$層の$j$番目のニューロンに入力する重み $w^{l+1}_{jk}$ を考えましょう。 逆伝播法（こちら）によると、 この重みに関する勾配は $a^l_k \delta^{l+1}_j$ と書けます。活性は全て正なので、 この勾配の符号は $\delta^{l+1}_j$ の符号と一致します。このことは、 もし $\delta^{l+1}_j$ が正ならば、全ての重み $w^{l+1}_{jk}$ は 勾配降下法で減少し、反対に $\delta^{l+1}_j$ が負ならば全ての $w^{l+1}_{jk}$ が減少することとなります。言い換えると、 同じニューロンに入力する全ての重みは一緒に増加するか一緒に減少するかしか できないのです。重みの一部だけ増加して残りの重みが減少するといった変化も 必要かもしれませんから、この性質は問題です。このことから、シグモイド関数を $\tanh$ のような正の値も負の値も取りうる活性関数で置き換えた方が良いように 思われます。実際、$\tanh$ は奇関数ですから、大雑把に言って隠れ層の活性は 正と負の両方にバランス良く分布するでしょう。それによって、 重みの更新に系統的なバイアスが掛かるのが避けられるでしょう。

  この議論はどの程度真面目に考えるべきでしょうか？この議論は示唆的ですが ヒューリスティックですし、tanhニューロンがシグモイドニューロンより高性能である ことの厳密な証明にはなっていません。ここで説明した問題を補うような良い性質を、 シグモイドニューロンが備えているのでしょうか。実際のところ多くの課題に対して、 tanhニューロンはシグモイドニューロンと比べて良くても僅かな改善しかしないことが 経験的に知られています。残念ながら、いかなる問題に対しても、 学習を最速化する、あるいは汎化性能を最大化するニューロンの種類を決定する 規則は存在しないのです。

  シグモイドニューロンのもう一つの変種は、Rectified Linear Unit あるいは ReLU と呼ばれるものです。入力 $x$, 重みベクトル $w$, そして バイアス $b$ が与えられた時、ReLUの出力は \begin{eqnarray} \max(0, w \cdot x+b). \tag{105}\end{eqnarray} と書けます。グラフにすると、次のようになります：

  明らかにシグモイドともtanhとも相当異なる形をしています。 しかし、シグモイドやtanhと同様、ReLUを使ったニューラルネットワークは 任意の関数を計算可能であることが知られており、逆伝播法や確率的勾配降下法を用いて 訓練できます。

  シグモイドやtanhニューロンよりもReLUが力を発揮できるのは どのような場面でしょうか？画像認識に関する最近の研究によると* *関連する文献としては、 Kevin Jarrett, Koray Kavukcuoglu, Marc'Aurelio Ranzato, Yann LeCunによる What is the Best Multi-Stage Architecture for Object Recognition? (2009), Xavier Glorot, Antoine Bordes, Yoshua Bengio による Deep Sparse Rectifier Neural Networks (2011), そして、Alex Krizhevsky, Ilya Sutskever, Geoffrey Hinton による ImageNet Classification with Deep Convolutional Neural Networks (2012) 等があります。これらの文献では、ReLUを用いたニューラルネットワークで 出力層、コスト関数、正規化等をどう設計すべきかという重要な点について詳細な議論を 行っています。ここで行う簡単な説明では、そのような詳細は省略します。 また、これらの論文では、ReLUの長所も短所も詳細に議論しています。 その他に有益な論文としては、Vinod Nair と Geoffrey Hinton による Rectified Linear Units Improve Restricted Boltzmann Machines (2010) があります。 この論文では、ニューラルネットワークに対する少々違ったアプローチにおいて正規化線形 ユニットを使うご利益を議論しています。 多くのニューラルネットワークでReLUの大きなご利益が得られるそうです。 しかし、tanhニューロンの場合もそうでしたが、ReLUをいつ、そしてなぜ 使うべきなのか、という問いに対しては、未だに深い理解は得られていません。 幾つかの論点を概観しておきましょう。まず、シグモイドニューロンの学習が遅くなるのは、 ニューロンが飽和している時、すなわち、ニューロンの出力が $0$ か $1$ に近いときです。 この章で何度も見てきたように、$\sigma'$ という因子が勾配を小さくしてしまうことで 学習が遅くなるのでした。tanhニューロンも飽和してしまうと同様の問題にぶつかります。 反対に、ReLUは重み付き入力値を大きくしても飽和することがないでしょう。 そのため、飽和に伴った学習速度の低下を起こさないのです。一方で、ReLUへの 入力が負の値を取るときには、勾配がゼロになります。そのため、ニューロンは学習を 完全にやめてしまうでしょう。この2つは、いつ、なぜ、ReLUが 優れているのかという問題の理解を妨げているたくさんある要因の一部に過ぎません。

  ここまで私は、活性関数の選び方に関する確固とした理論が存在しないことを 強調してきました。しかし現実は、ここまで説明してきたよりもさらに困難です。 というのも、活性関数の選択肢は無限にあるのですから。 与えられた問題に対する最良の選択はどれか？どれが最高の試験精度を達成するか？ どれが学習を最速で行うか？これらの問いに対して、真に深く系統的な 研究が行われていないことに私は驚いています。理想的には、活性関数の選び方を 教えてくれる理論があってもおかしくないはずです。とはいえ、完全な理論が 無いからといって、私たちが立ち止まる必要はありません！ 既に強力なツールはたくさんあるので、それらを使えば多くのことを成せる はずなのですから。この本の残りの部分では、シグモイドニューロンを使い続ける ことにします。シグモイドニューロンも十分に強力ですし、ニューラルネットワークの 中核を成すアイデアを具体的に示すには良い道具だからです。 しかし、同じアイデアはシグモイドニューロンに限らず他の種類のニューロンにも 当てはまることは覚えておいてください。そして時には他のニューロンの方が 高い性能を発揮する場合もあることを心に留めておいてください。

  ニューラルネットワークに関する「お話」について

  質問： 機械学習の手法は数学的にほとんど理解されておらず、 それが上手くいくかどうかは経験的な裏付けしかありません。 これらの手法を利用したり研究したりしたい場合、どうやって取り掛かれば良いのですか？ また、これら機械学習の手法が破綻するのはどのような状況ですか？

  回答： まず、手元にある理論的な道具はとても貧弱であることを認める必要があります。 時には、ある特定の手法が効果的に働くであろうという、 数学的な直感に基づく予測が可能な場合もあります。 また時には、私たちの直感が誤りだと後になって気づくこともあります。（中略） 質問はこう言い換えるべきでしょう： この手法はこの特定の問題に対してどのくらい効果的ですか？ そして、この手法が上手く働く問題はどのくらいたくさんありますか？

  - Question and answer, ニューラルネットワーク研究者 Yann LeCun

  かつて量子力学の基礎付けに関する会議に出席した時、発言者達が非常に興味深い習慣を 持っていることに気づきました。発表が終わると、聴衆からの質問がしばしば 「あなたの視点にはとても共感しました。しかし、...」から始まるのです。 量子力学の基礎付けは、私が普段研究している分野ではありません。 この質問のしかたに気づいたのは、この分野以外の研究会で発表者の視点に共感を表現する 質問者を見かけることは皆無だからです。当時は、この種の質問が蔓延るのは、 この分野がほとんど進展していなくて、皆が無駄な努力をしていることの現れだろうと 考えていました。後になって、この評価は厳しすぎたことに気づきました。 発表者は人類の頭脳が向き合った中で最も難しい問題の一つに取り組んでいたのです。 進展が遅いのは当たり前です！そして、はっきりと新しい進展が無かったとしても、 人々がどう考えているのかについて最新の話を聞くことには価値があったのです。

  この本を読んでいて、読者の皆さんは「とても共感しました」と同種の決まり文句に 気づいたかもしれません。何かを説明しようとする度に、「ヒューリスティックに」や 「大雑把に言って」等と口にした後、何らかの現象等を説明するお話を続けました。 これらのお話はもっともらしいですが、経験的な証拠としては非常に心許ないものです。 ニューラルネットワークの研究に関する文献等を調べてみると、多くの論文に 同様の体裁を取ったお話が見られることでしょう。 それも、多くの場合証拠としてはとても弱いものです。 この状況はどう理解するべきでしょうか？

  科学の多くの分野、特に単純な現象を扱う分野で、非常に一般的な仮説に対する、 非常に強固で非常に信頼度の高い証拠が得られます。しかし、ニューラルネットワークの場合、 多数のパラメータやハイパーパラメータが存在し、それらが極度に複雑に絡み合っています。 このように非常に複雑な系では、信頼できる一般的な議論を行うことは非常に困難です。 ニューラルネットワークを完全に一般的に理解することは、量子力学の基礎付けのように、 人類の頭脳の限界に挑戦する課題です。一般論を展開する代わりに、 その具体例を幾つか取り上げて、一般的な主張がもっともらしいかどうかの議論を行うのです。 そして時には、後の検証で修正されたり破棄されたりする結果となるのです。

  ヒューリスティックに頼るという事実が問題の困難さを示していると見ることもできます。 例えば、ドロップアウト法の説明で引用 した文章を思い出してみましょう* *出典は Alex Krizhevsky, Ilya Sutskever, Geoffrey Hinton による ImageNet Classification with Deep Convolutional Neural Networks (2012) です。： 「この手法はニューロン間の複雑な相互適合を軽減します。 というのも、 訓練に際してニューロンは特定の他のニューロンを 頼りにすることができないからです。 したがって、あるニューロンは、 ランダムに選ばれた他のニューロンと一緒にされても役に立つような、 データが持つより強固な特徴を学ぶように強制されるのです。」 この主張は内容が豊富で刺激的です。この主張を一つ一つ検証していくこと、 すなわち、この主張のどこが正しくどこが誤っていて、どのような変更や修正が必要なのか 明らかにしていくことで、立派な研究ができるでしょう。 実際、ドロップアウトやその変種について、それが上手くいくメカニズムや限界を調べている 研究者の一団がいます。彼らは、この本でここまで議論してきたヒューリスティックに 取り組んでいるのです。それぞれのヒューリスティックは（潜在的に）ある現象を 説明してくれるだけでなく、それ自体がより詳しく調べて理解すべき課題となるのです。

  もちろん、一人の人間がこれら全てのヒューリスティックな議論を詳しく調べるには、 全く時間が足りません。ニューラルネットワークの学習についてエビデンスに基づいた強力な 理論を構築するには、これから何十年も（あるいはもっと）時間が掛かるでしょう。 では、私たちはヒューリスティックな説明を根拠に欠ける曖昧なものとして捨て去るべきだと いうのでしょうか？そんなことはありません！むしろ、そのようなヒューリスティックには、 私たちの思考を刺激し導くという重要な役割があるのです。 これは大航海時代のようなものです：初期の探検家たちは、時に完全な誤解に基づいて探検し、 そして新しい発見をしてきたのです。それらの誤解は、後になって地理に関する知識が 蓄積されるにつれ、修正されてきました。ニューラルネットワークに対する理解が今日非常に 貧弱であるように、何かをほとんど理解できていない時こそ、一歩ずつ完全に正しい思考を 進めるよりも、大胆に探検していくことが重要なのです。ですから、この本でしてきた ヒューリスティックな議論は、ニューラルネットワークについて考える際の便利なガイドである と考えるべきです。ただし、それらの話に限界があることも認識し、 どの程度強く裏付けられているのかを意識しておく必要があります。 言い換えると、ニューラルネットワークを使っていく上で発想の助けになるお話と、 実際に起こっていることを明らかにする厳密で詳細な検討が必要なのです。